A pump is used to pump a liquid of density ρ continuously through a pipe of cross, sectional area A. If liquid is flowing with speed v, then average power of pump is
13ρAV2
12ρAV2
2ρAV2
12ρAV3
The correct Answer is:D
To find the average power of the pump used to pump a liquid of density ρ through a pipe of cross-sectional area A at speed v, we can follow these steps:
Step 1: Calculate the mass flow rate
The mass flow rate dmdt can be expressed in terms of the density ρ, the cross-sectional area A, and the speed v of the liquid.
Using the relationship:
dmdt=ρ⋅Volume flow rate
The volume flow rate can be calculated as:
Volume flow rate=A⋅v
Thus, we have:
dmdt=ρ⋅(A⋅v)=ρAv
Step 2: Determine the kinetic energy of the liquid
The kinetic energy KE of a mass m moving with velocity v is given by:
KE=12mv2
To find the kinetic energy per unit time (which relates to power), we need to express m in terms of the mass flow rate:
KE=12(dmdt⋅t)v2
Substituting dmdt=ρAv into the equation gives:
KE=12(ρAv)v2⋅t
Step 3: Calculate average power
Average power Paverage is defined as the energy per unit time. Therefore, we can express it as:
Paverage=KEt=12(ρAv)v2⋅tt
This simplifies to:
Paverage=12ρAv3
Final Result
Thus, the average power of the pump is:
Paverage=12ρAv3
---
The mass flow rate dmdt can be expressed in terms of the density ρ, the cross-sectional area A, and the speed v of the liquid.
dmdt=ρ⋅Volume flow rate
The volume flow rate can be calculated as:
Volume flow rate=A⋅v
Thus, we have:
dmdt=ρ⋅(A⋅v)=ρAv
The kinetic energy KE of a mass m moving with velocity v is given by:
KE=12mv2
To find the kinetic energy per unit time (which relates to power), we need to express m in terms of the mass flow rate:
KE=12(dmdt⋅t)v2
Substituting dmdt=ρAv into the equation gives:
KE=12(ρAv)v2⋅t
Average power Paverage is defined as the energy per unit time. Therefore, we can express it as:
Paverage=KEt=12(ρAv)v2⋅tt
This simplifies to:
Paverage=12ρAv3
Thus, the average power of the pump is:
Paverage=12ρAv3
Topper's Solved these Questions
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - Assignment (SECTION - B)
35 Videos
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - Assignment (SECTION - C)
80 Videos
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - EXERCISE
37 Videos
- WAVESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WAVESEXERCISE - ASSIGNMENT ( SECTION-D ( Assertion - Reason Type Questions ))
12 Videos
Similar Questions
An engine pumps liquid of density ρ continuously through a pipe of cross-section area A. If the speed with which liquid passes through the pipe is v, then the rate at which kinetic energy is being imparted to the liquid by the pump is
View SolutionAn engine pumps a liquid of density 'd' continuously through a pipe of area of cross-section A. If the speed with which the liquid passes through a pipe is v, then force exerted on liquid.
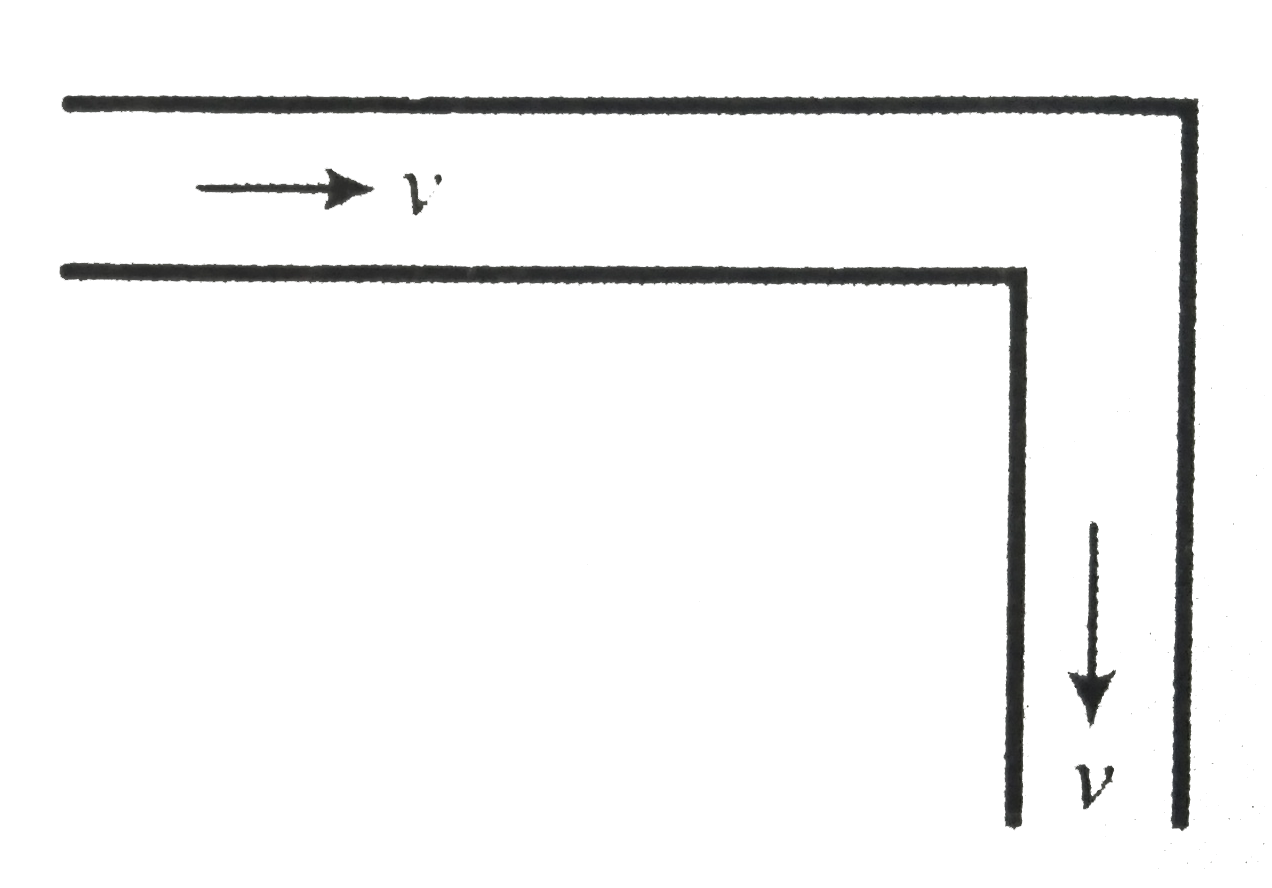
View SolutionA liquid of density ρ is flowing with a speed v through a pipe of cross sectional area A. The pipe is bent in the shape of a right angles as shown. What force should be exerted on the pipe at the corner to keep it fixed?
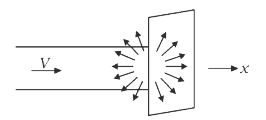
View SolutionA liquid of density ρ is flowing with a speed V through a pipe of cross sectional area A. What force does the liquid stream exert on wall in x direction if it splashes in the form of a circle after it hits the wall?
View SolutionReynolds number for a liquid of density ρ, viscosity η and flowing through a pipe of diameter D, is given by
View SolutionA non viscous liquid of density ρ is filled in a tube with A as the area of cross section, as shown in the figure. If the liquid is slightly depressed in one of the arms, the liquid column oscillates with a frequency

View SolutionAn incompressible liquid of density ρ is enclosed with two frictionless pistons one of cross-sectional area A and the other of 4 A. When the narrow piston moves out by a distance.
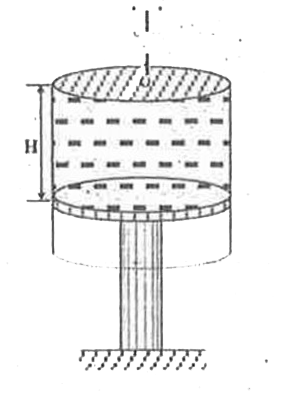
View SolutionIn the adjacent figure a cylindrical vessel of mass M and cross - sectional area A is placed inverted on a fixed smooth piston of same cross - sectional area fixed to the ground . The space between the cylinder and priston is completely filled with liquid of density ρ . There is a small office of cross - sectional area a (a<<A) at the top top portion of this vessel . ( intially length of the liquid column in the vessel is H )
Speed of the liquid with which it comes out of the vessel is

View SolutionIn the adjacent figure a cylindrical vessel of mass M and cross - sectional area A is placed inverted on a fixed smooth piston of same cross - sectional area fixed to the ground . The space between the cylinder and priston is completely filled with liquid of density ρ . There is a small office of cross - sectional area a (a<<A) at the top top portion of this vessel . ( intially length of the liquid column in the vessel is H ).Find the speed of the vessel with which it move
View SolutionA viscous liquid flows through a horizontal pipe of varying cross-sectional area. Identify the option which correctly represents the variation of height of rise of liquid in each vertical tube
View Solution
