The magnitude of the net force exerted in the x direction on a 2.50-kg particle varies with the time as shown in fig., find (a) the impules of the force. (b) the final velocity the particle attains if it is originally at rest,
(c ) its final velocity if its original velocity is −2.0ms−1, and
(d) the average force exerted on the particle for the time interval between 0 and 5 s.

(a) The impulse is to the right and equal to the area under the F−t graph I={[5+1]/2}×4=12Ns
(b) m→vi+→Ft=m→vf
⇒2.5×0+12=(2.5)v⇒v=4.8ms−1
( c) From the same equation,
⇒2.5×(−2)+12=(2.5)v⇒v=4.8ms−1
(d) F_(avg)Delta t=12.0implies F_(avg)=2.40N.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Exercise 6.235videos
NEWTON'S LAWS OF MOTION 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Exercise 6.319videos
NEWTON'S LAWS OF MOTION 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Solved Examples11videos
NEWTON'S LAWS OF MOTION 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE10videos
MISCELLANEOUS VOLUME 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type1videos
NEWTON'S LAWS OF MOTION 2
Similar Questions
The magnitude of force acting on a particle moving along x-axis varies with time (t) as shown in figure. If at t = 0 the velocity of particle is v0, then its velocity at t=T0 will be
 View Solution
View SolutionForce acting on a particle varies with displacement as shown is Fig. Find the work done by this force on the particle from x=−4m to x = + 4m.
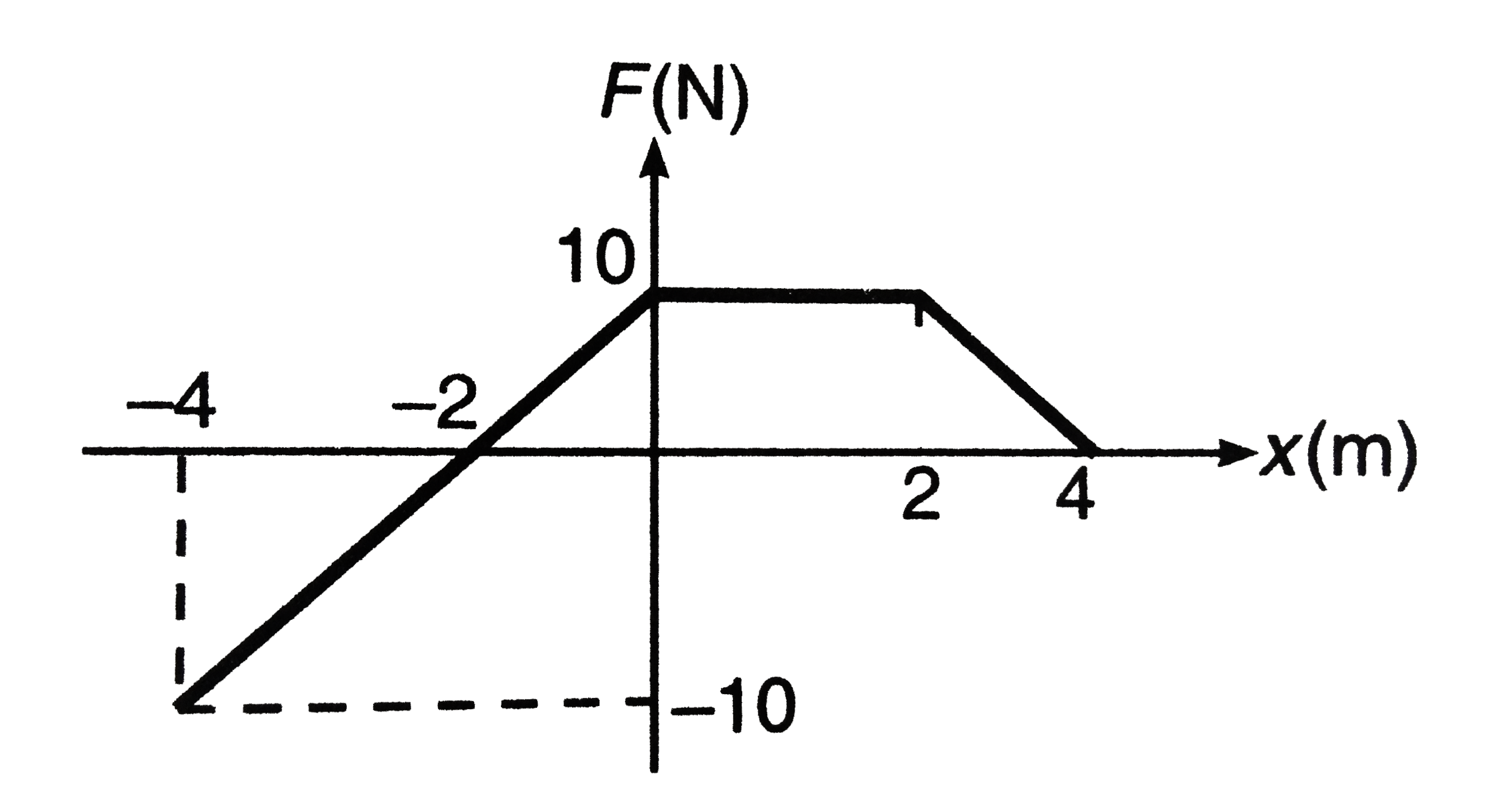 . View Solution
. View SolutionIf the displacement of a particle varies with time as x=5t2+7t.
Then find its velocity.View SolutionPower of a force acting on a block varies with time t as shown in figure. Then, angle between force acting on the block and its velocity is
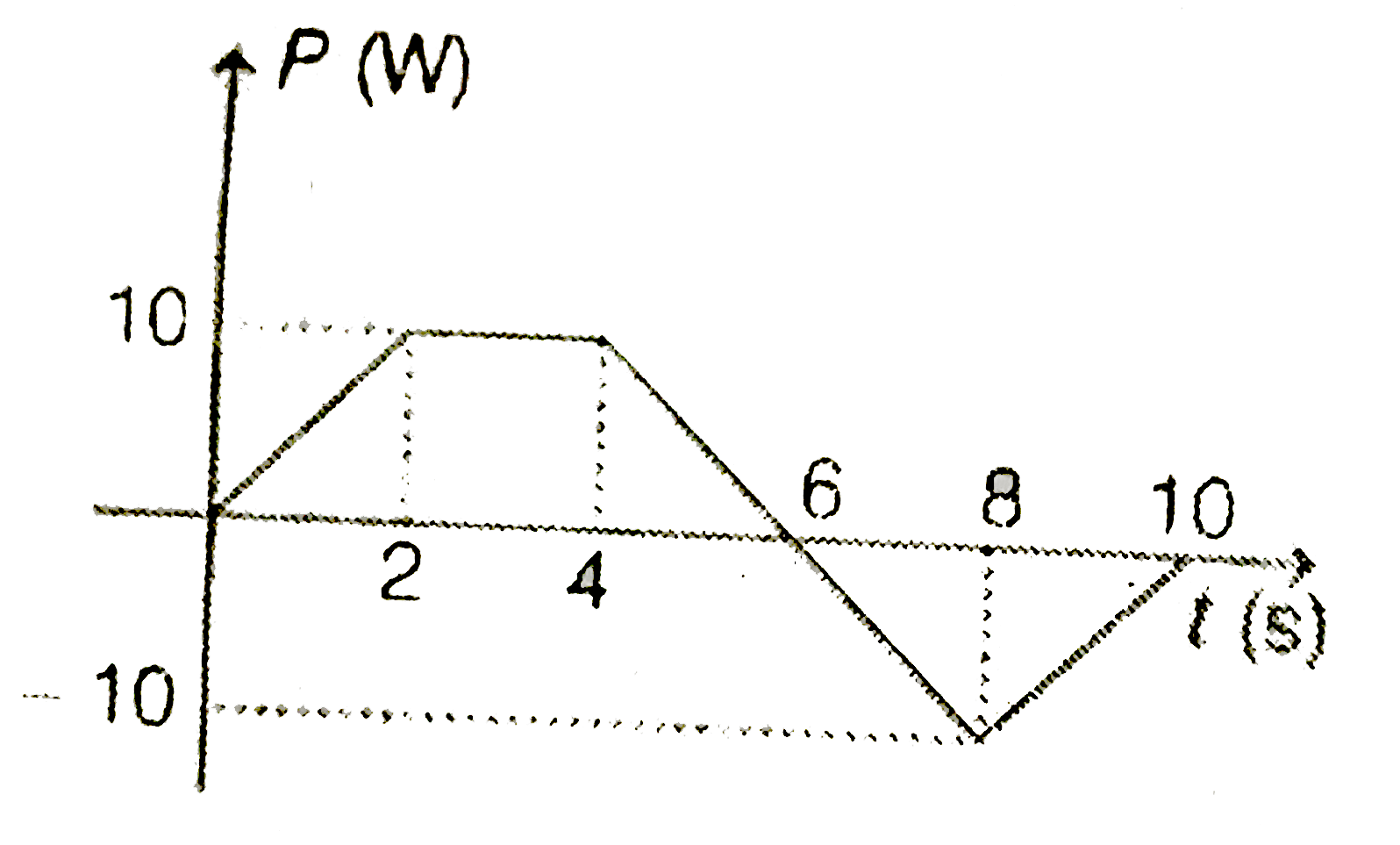 View Solution
View SolutionA particle mass parallel to x-axis with constant velocity v as shown in the figure. The angular velocity of the particle about the origin O

View SolutionThe velocity of a particle varies with its displacement as v=(√9−x2)ms−1.
Find the magnitude of the maximum acceleration of the particle.View SolutionA particle starting from rest attains a velocity of 50ms−1 in 5 s. The acceleration of the particle is
View SolutionA particle moving with velocity →V is acted by the three forces shown by the vector triangle PQR. The velocity of the particle will :
 View Solution
View SolutionA point traversed 3/4 th of the circle of radius R in time t. The magnitude of the average velocity of the particle in this time interval is
View SolutionA particle of mass 2kg is initially at rest. A force starts acting on it in one direction whose magnitude changes with time. The force time graph is shown in figure. Find the velocity of the particle at the end of 10s.
 View Solution
View Solution

