A smooth ring A of mass m can slide on a fixed horizontal rod. A string tied to the ring passes over a fixed pulley B and carries a block C of mass M(=2m) as shown in figure. At an instant the string between the ring and the pulley makes an angle θ with the rod. a. Show that, if the ring slides with a speed v, the block descends with speed vcosθ, b. With what acceleration will the ring starts moving if the system is released from rest with θ=300
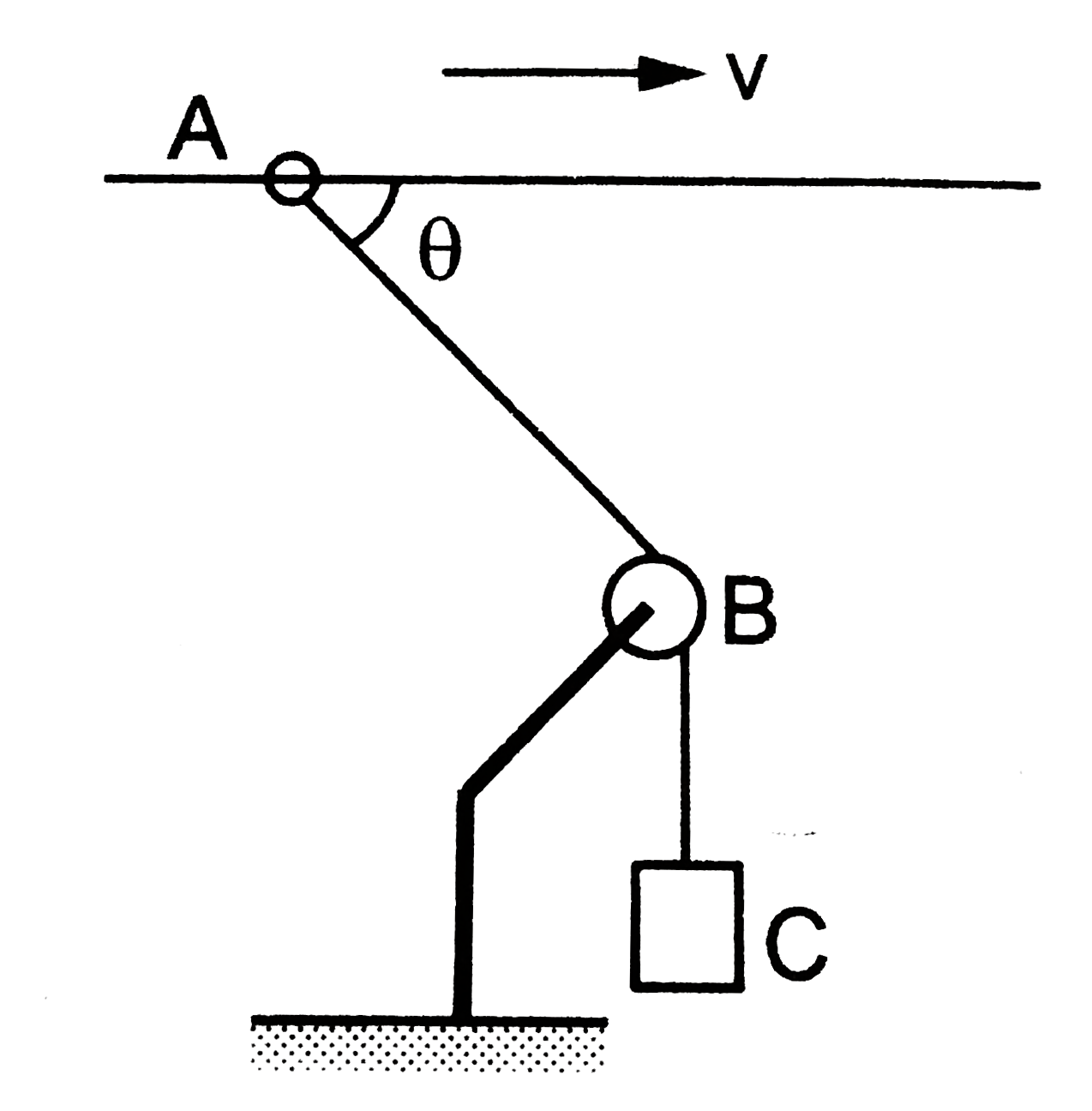
The correct Answer is:(b) 2g√35ms−2
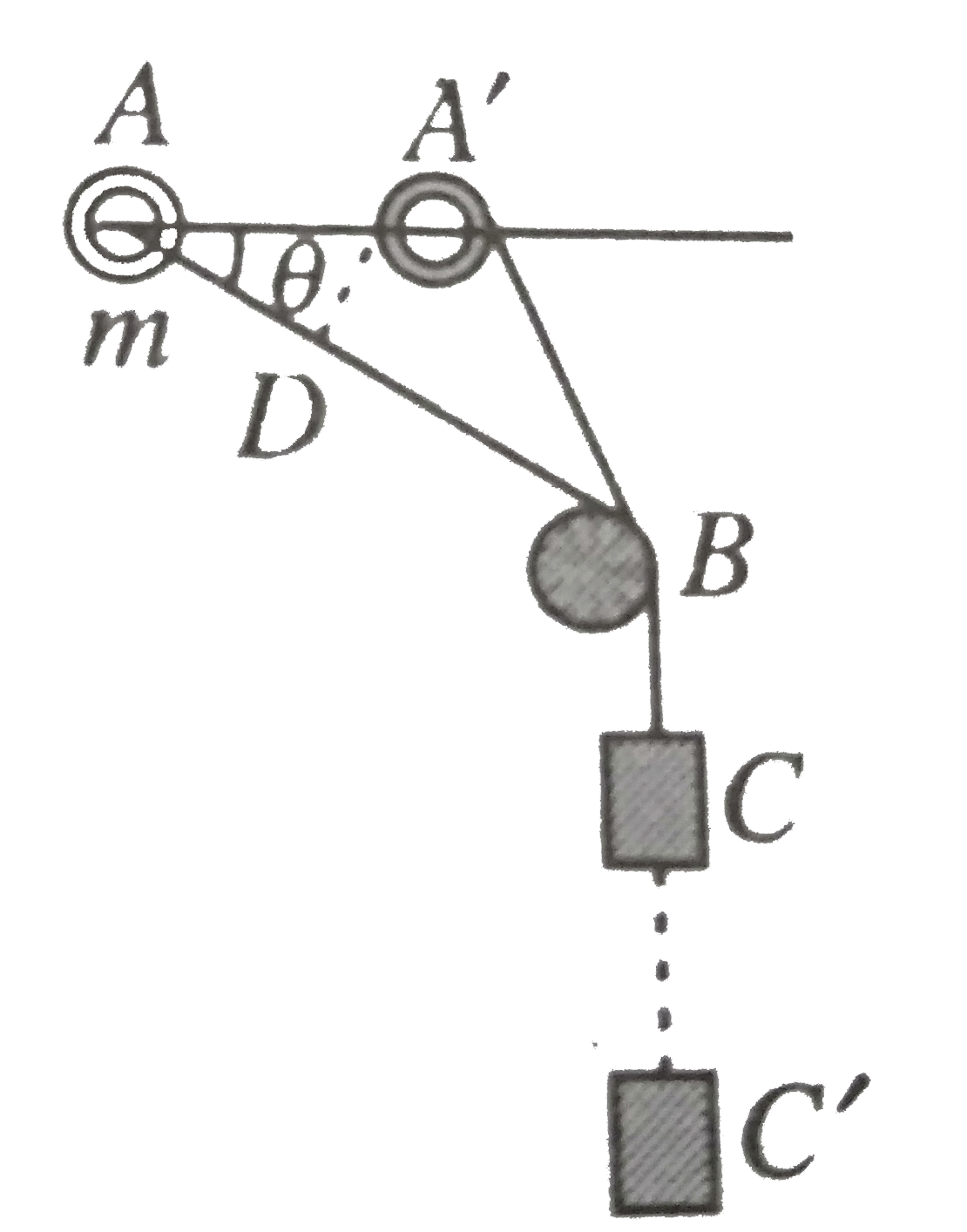
When ring slides form A and A' in time interval Δt, the block descends from C to C' as shown in fig. A' D is perpendicular by dropped from A' on AB. For small displacement , A'B=DB
Now as length of string is constant
AB+BC=A'B+BC'
or (AD+DB)+BC=A'B+BC'
AD=BC'−BC(∵A'B=DB)
or AA'cosθ=CC'
⇒AA'Δtcosθ=CC'Δt
i.e. velocity of ring ×cosθ= velocity of block
i.e., velocity of block C, vc=vcosθ ...(i)
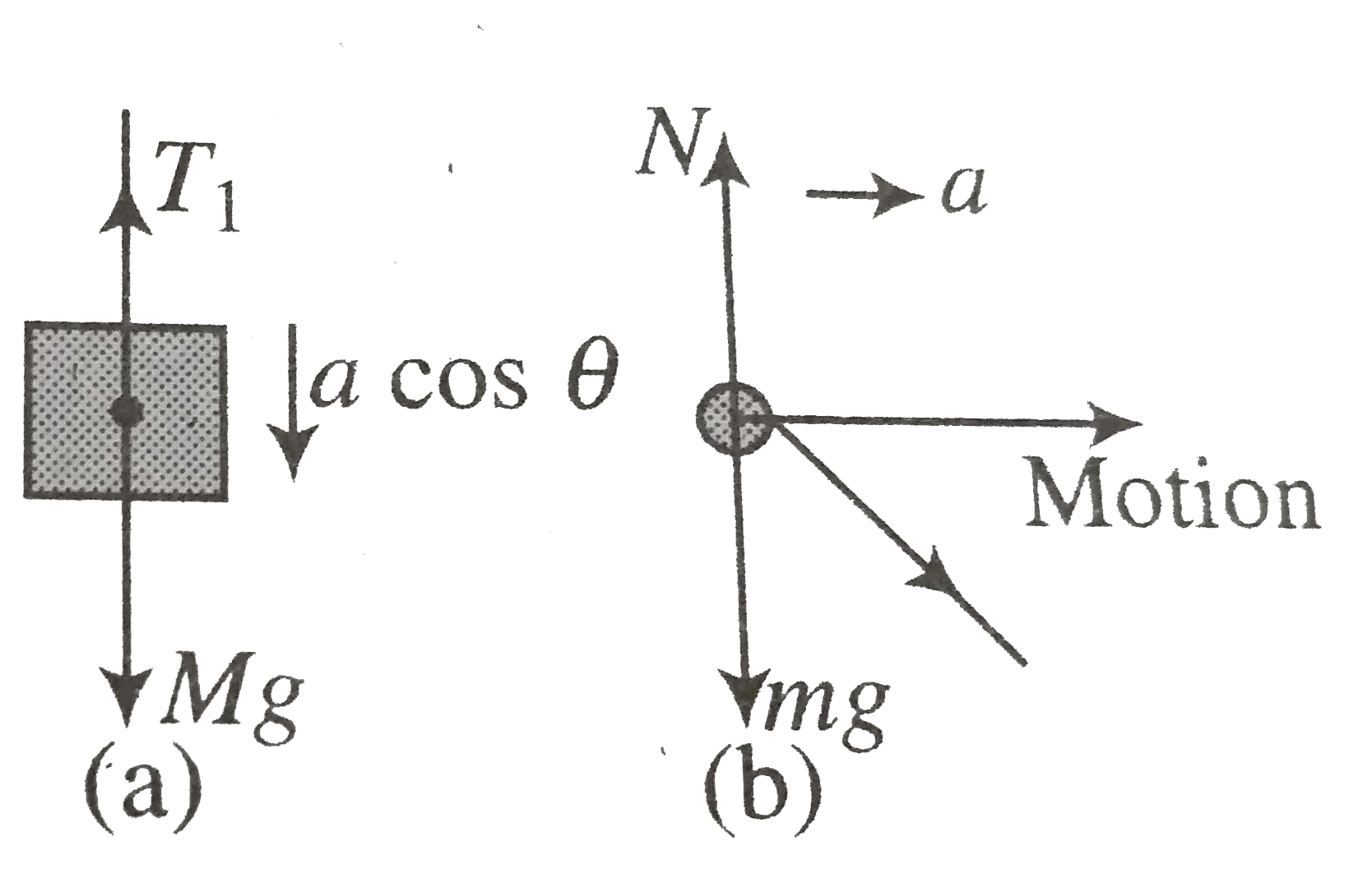
(b) If a is the initial acceleration of ring, then acceleration of block =acosθ.
Let T be the tension in the string at this instant. Then the free-body diagram of block is shown in fig.
(c ) Equation of motion of block M is
Mg−T−Macosθ ..(ii)
The free-body diagram of ring is shown in fig. Resolving T along horizontal and vertical, we have
Tcosθ=ma⇒T=macosθ...(iii)
Equation (ii) and (iii)give
a=Mgcosθm+Mcos2θ
=2mgcos30∘m+2mcos230∘=2g(√32)1+2×(34)=2g√35ms−2.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Single Correct75videos
NEWTON'S LAWS OF MOTION 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Multiple Correct11videos
NEWTON'S LAWS OF MOTION 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Exercise 6.413videos
NEWTON'S LAWS OF MOTION 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE10videos
MISCELLANEOUS VOLUME 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type1videos
NEWTON'S LAWS OF MOTION 2
Similar Questions
A string of negligible mass going over a clamped pulley of mass m supports a block of mass M as shown in the figure. The force on the pulley by the clamp is given by
 View Solution
View SolutionA block of mass m1 rests on a horizontal table. A string tied to the block is passed on a frictionless pulley fixed at the end of the table and to the other end of string is hung another block of mass m2. The acceleration of the system is
View Solution
Knowledge Check
- Question 1 - Select One
A string of negligible mass going over a clamped pulley of mass m supports a block of M as shown in the figure. the force on the pulley by the clamp is given by:
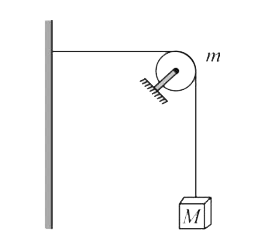 A√2MgB√2mgC√(M+m)2+m2gD√(M+m)2+M2g
A√2MgB√2mgC√(M+m)2+m2gD√(M+m)2+M2g
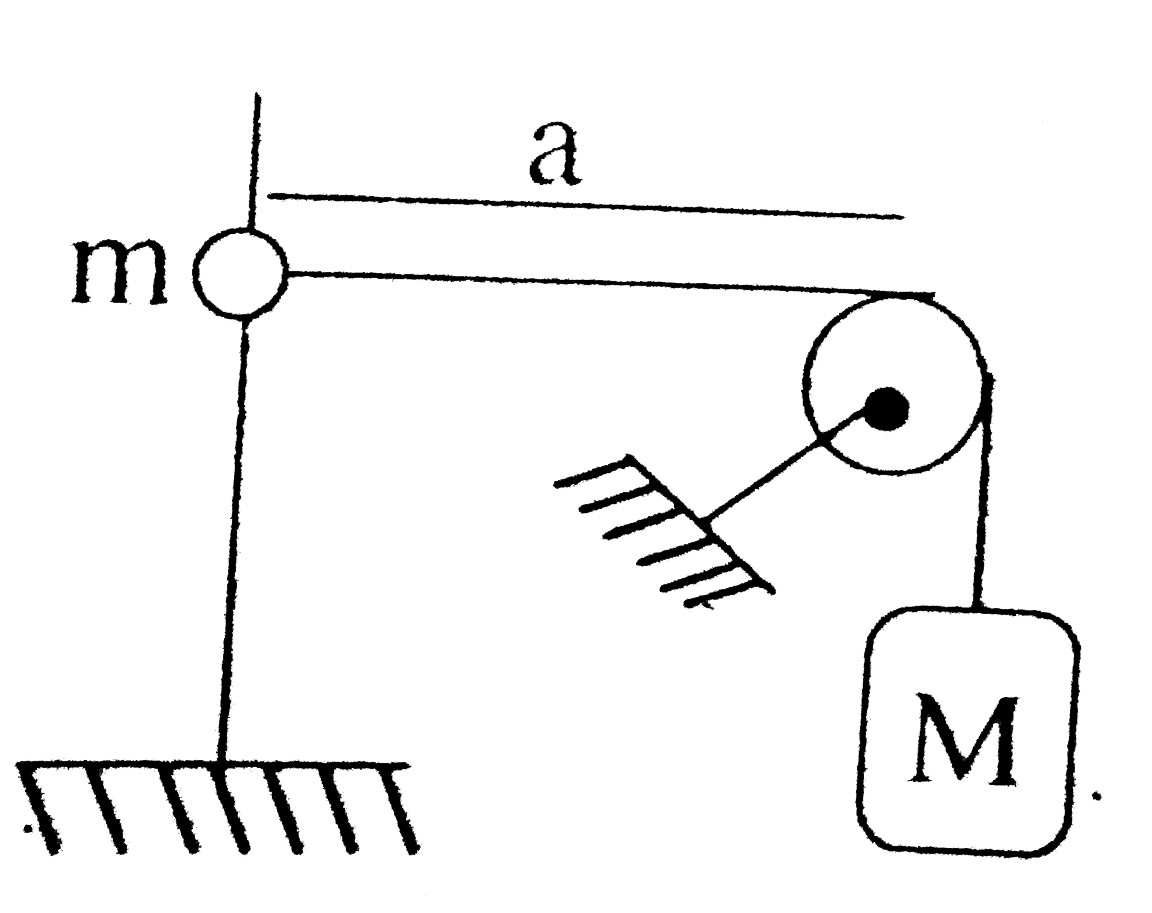
A ring of mass m can slide on the vertical smooth rod. Ring is connected by block with string as shown in figure. Pulley is of mass-less and smooth the system is released from reast. Initial tension in string isView SolutionA ring of mass m=1kg can slide over a smooth vertical rod. A light string attached to the ring passing over a smooth fixed pulley at a distance of L=0.7m from the rod as shown in figure.
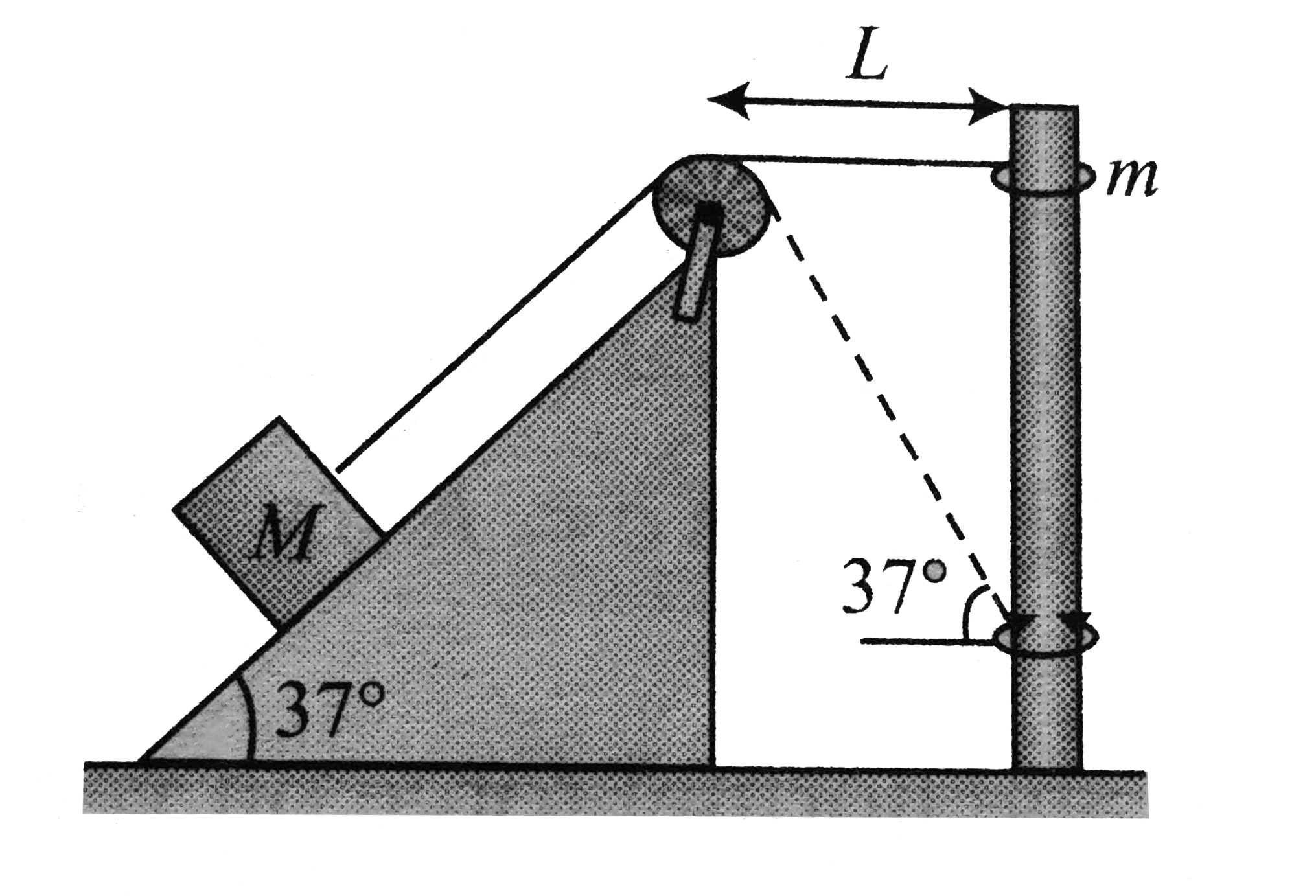
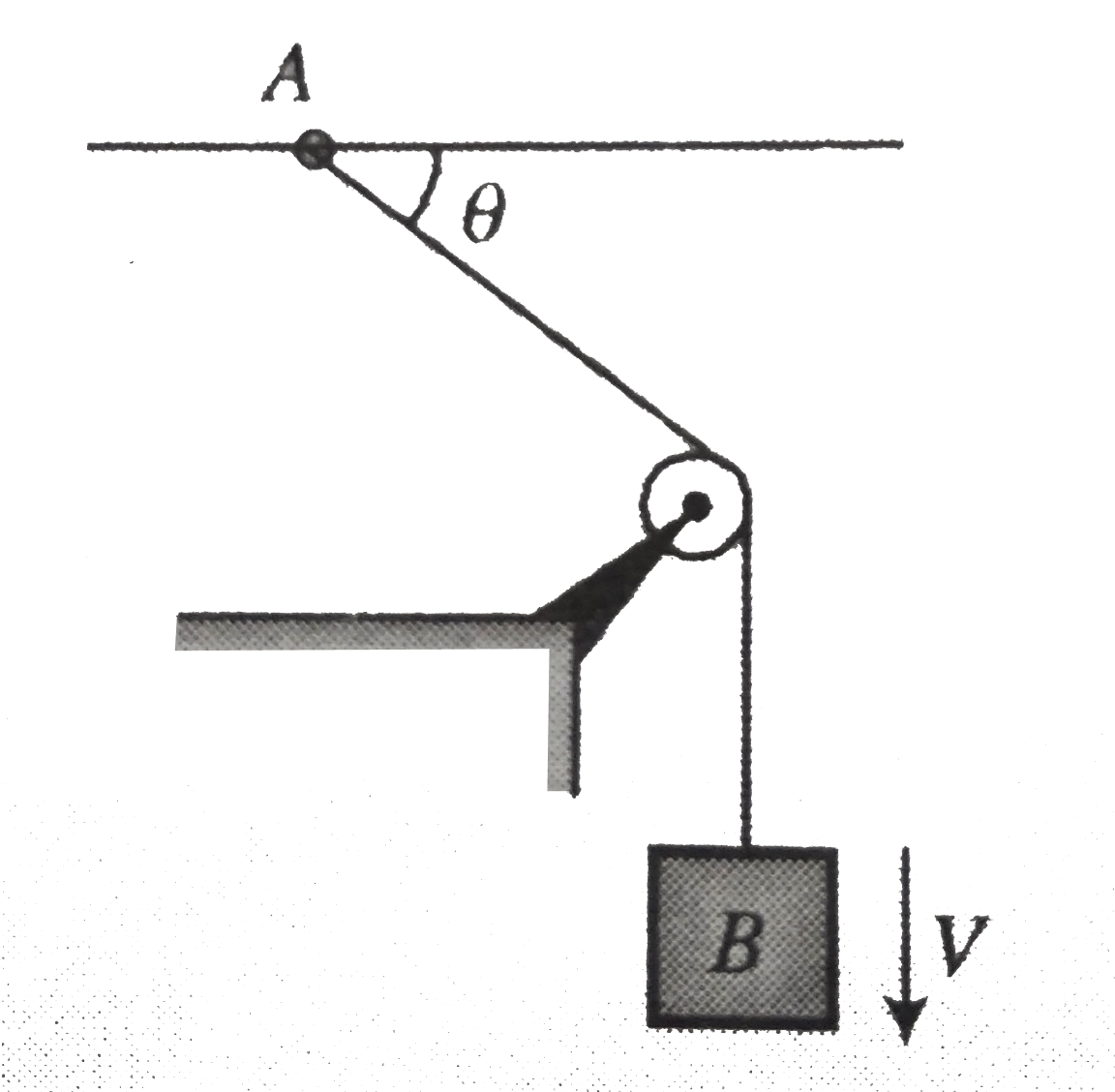
At the other end of the string mass M=5kg is attached, lying over a smooth fixed inclined plane of inclination angle 37∘. The ring is held in level with the pulley and released. Determine the velocity of ring when the string makes an angle (α=37∘) with the horizontal. [sin37∘=0.6]View SolutionA ring A which can slide on a smooth wire is connected to one end of a string as shown in fig. Other end of the string is connected to a hanging mass B. Find the speed of the ring when the string makes an angle θ with the wire and mass B is going down with a velocity v.
 View Solution
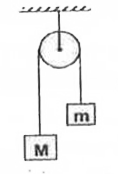
View SolutionTwo masses m and M(m<M) are joined by a light string passing over a smooth and light pulley (as shown)
 View Solution
View SolutionA ring of mass m = 0.3kg can slide freely on smooth vertical rod. A light and inextensible string is connected to the ring and passes over a smooth and fixed pulley as shown in the figure. The distance of the pulley from the rod is 0.8m and the other end of the string is connected to a block of mass M = 0.5kg. The ring is held in level with pulley and then released from rest.
The distance by which the ring moves down before coming to rest for the first time is 0.75K. Find K.
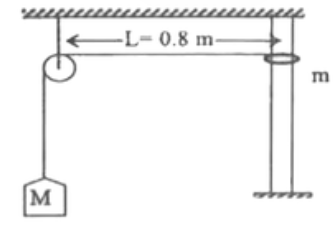 View Solution
View SolutionTwo blocks of masses m and 3m are connected by an inextensible string and the string passes over a fixed pulley which is massless and frictionless. A bullet of mass m moving with a velocity 'u' hits the hanging block of mass 'm' and gets exbedded in it. Find the height through which block A rises after the collision.
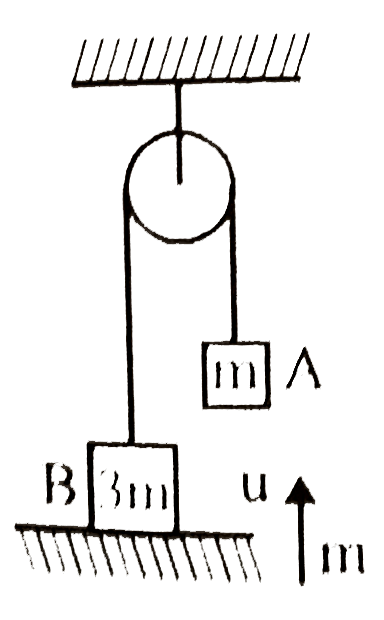 View Solution
View SolutionA block of mass M is pulled on a smooth horizontal table by a string making an angle θ with the horizontal as shown in figure. If the acceleration of the block is a, find the force applied by the string and by the table N on the block.
 View Solution
View Solution

