In fig two block of mass mAandmB are rotating at radius r kept on a rough table consider friction (μ) between all the contact surface pulley is frictionless determine the angular speed of the turn table for which the blocks just begin to slide

Equation for block B :
∑Fx=T+μsmA+mBg+μsmAg−mBrω2=0
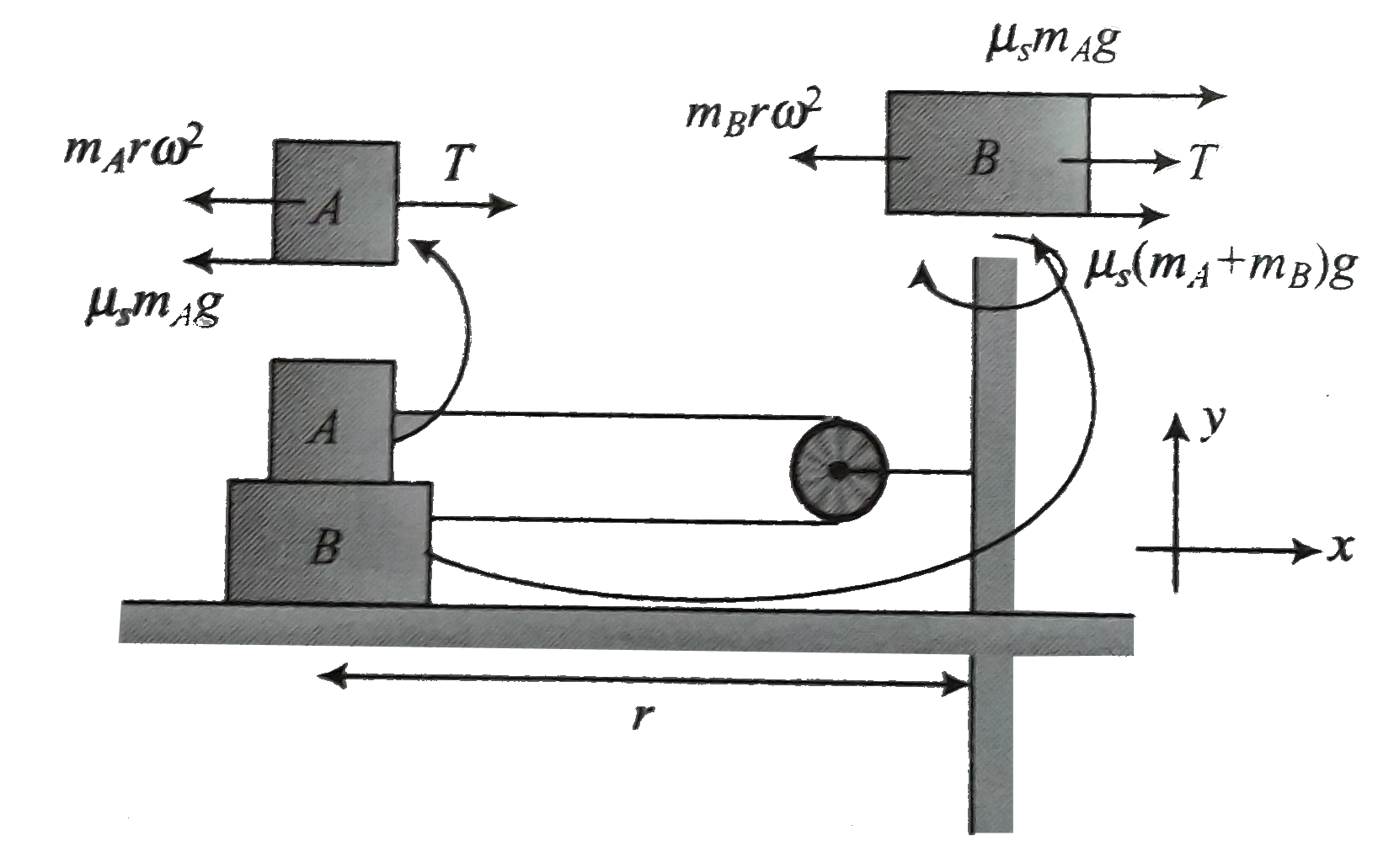
Equation for block A :
∑Fx=T−μs(mA)g−(mArω2)=0 ...(i)
From equation (i) and (ii) , we climinate T as obtain
2μsmAg+μ(mA−mB)=(mB−mA)rω2
ω=[μsg(3mA+mB)r(mB−mA)]1/2
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Solved Examples12videos
NEWTON'S LAWS OF MOTION 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Exercise 7.125videos
NEWTON'S LAWS OF MOTION 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Integer5videos
NEWTON'S LAWS OF MOTION 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE2videos
PROPERTIES OF SOLIDS AND FLUIDS
Similar Questions
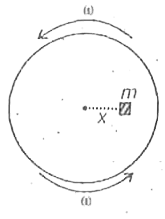
A block of mass m kept on rough horizontal turn table at a distance x from the centre. If the coefficient of friction between the table and block is μ then maximum speed of point P on turn table so that the block does not slip is
 View Solution
View SolutionA block of mass m is kept on horizontal turn table at x distance from the centre. If coefficient of friction between block and surface of turn table is μ, then maximum angular speed of the table so that block does not slip
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A block of mass m rests on a rough inclined plane. The coefficient of friction between the surface and the block is µ. At what angle of inclination θ of the plane to the horizontal will the block just start to slide down the plane?
Aθ=tan−1μBθ=cos−1μCθ=sin−1μDθ=sec−1μ
A block of mass m is pulled by a force of constant power P placed on a rough horizontal plane. The friction coefficient between the block and the surface is μ. Then
View SolutionA block of mass m is moving on a rough horizontal surface. μ is the coefficient of kinetic friction between the block and the surface. What is the net force exerted by the surface on the block?
View SolutionA disc of mass m and radius R rotating with angular speed ω0 is placed on a rough surface (co-officient of friction =μ). Then
 View Solution
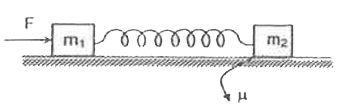
View SolutionTwo blocks of masses m1 and m2 are connected by a spring of stiffness k. The coefficient of friction between the blocks and the surface is μ. Find the minimum constant force F to be applied to m1 in order to just slide the mass m2.
 View Solution
View SolutionTwo block of masses m and M are connected by a chord passing around a frictionless pulley which is attached to a rotating frame , which rotates about a vertical axis with an angular velocity ω If the coefficient of friction between the two masses and the surface are μ1 and μ2 respectively determine the value of ω at which the block starts sliding radially (M>m)
 View Solution
View SolutionA block m1 strikes a stationary block m3 inelastically. Another block m2 is kept on m3. Neglecting the friction between all contacting surfaces, calculate the fractional decrease in KE of the system in collision.
View SolutionTwo block , with masses m1 and m2 are staked as shown in fig and placed on a frictionless horizontal surface . There is a friction between the two block .An external force of magnitude F is applied to the top block at an angle α below the horizontal . The coefficient of friction between m1 and m2 are μs
b. If the two blocks move together, find their acceleration
b . Calculate the maximum value of force so that blocks will move together
 View Solution
View Solution

