A pendulum initially is at rest in vertical position. The bob is pulled slowly towards right. Find the change in gravitational potential energy of the pendulum bob of mass m as the function of x.
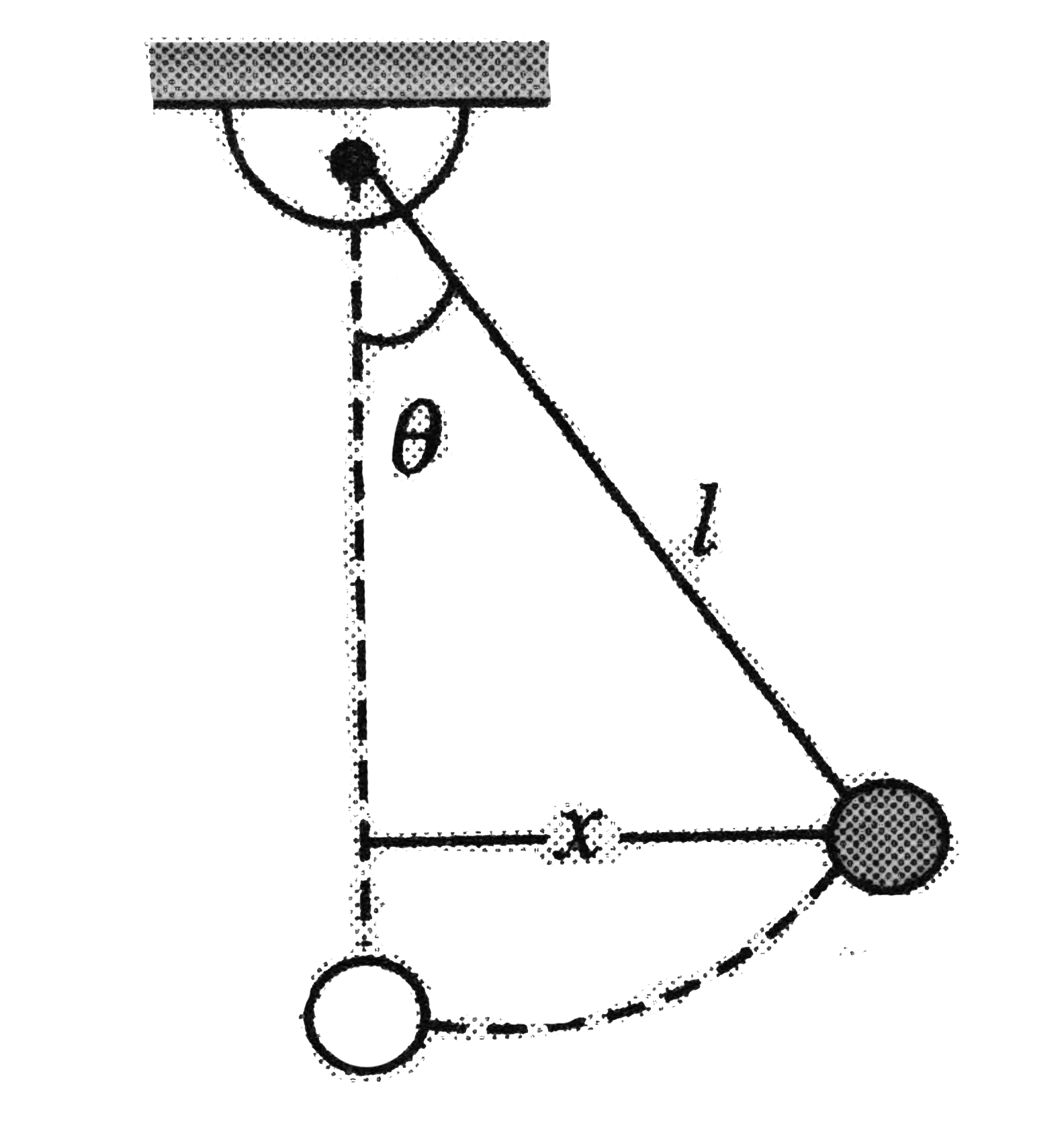
The change in potential energy of a particle depends upon the vertical displacement of the particle with respect to initial position. It increases for upward displacement and decrease for downward displacement. Here the change in potential energy of the bob at any angular position θ is
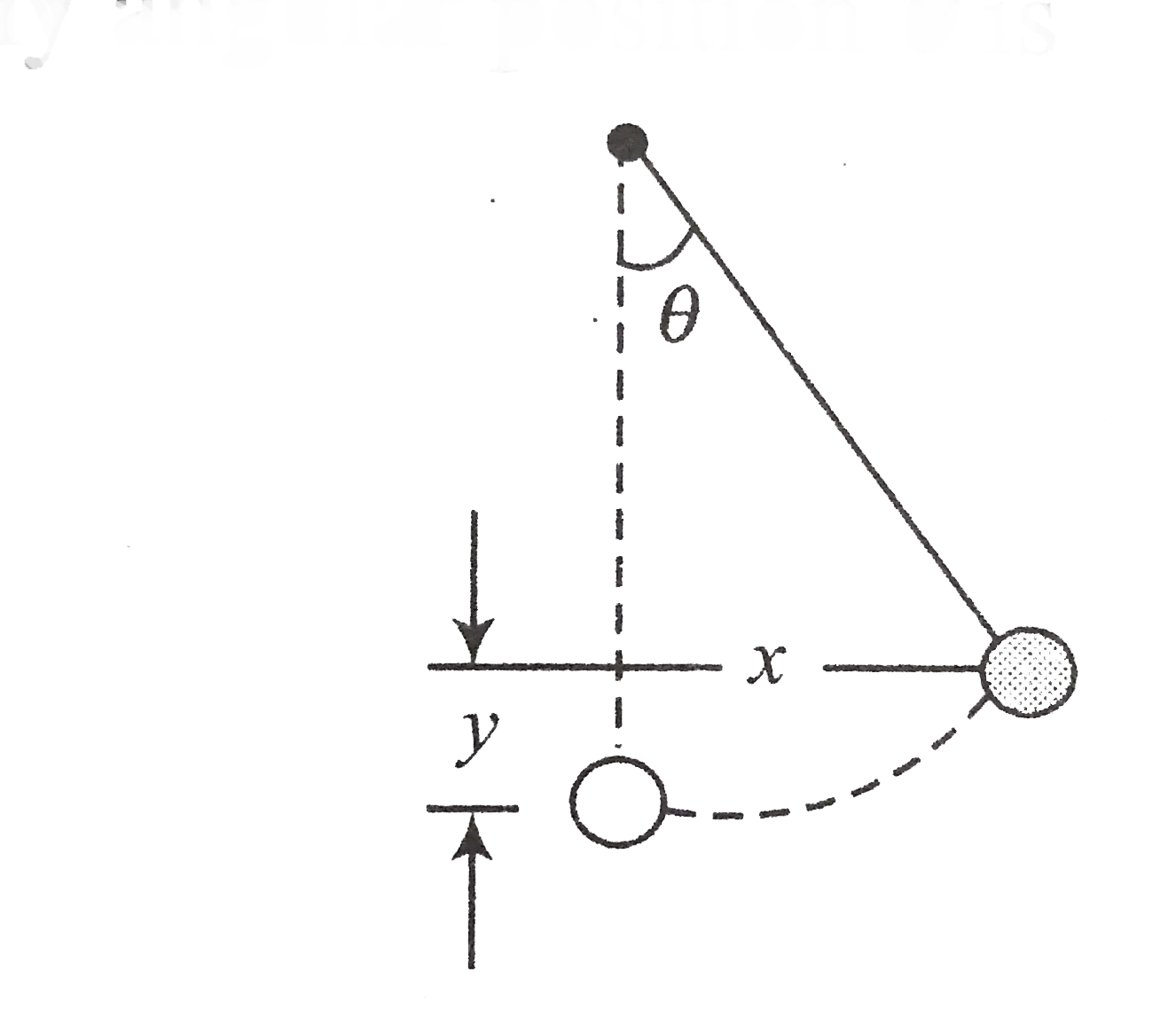
ΔU=mgl(1−cosθ) (i)
cosθ=√l2−x2l (ii)
Using Eqs (i) and (ii), we get
U=mgl(1−√1−x2l2)
For writing potential energy of point mass, we take earth surface as reference point where we take potential energy zero.
For a regular-shaped body where mass is distributed uniformly, we take as mass concentrated at its geometrical counter. This point is called center of gravity. We can replace the body a point mass placed at the centre of gravity.
Topper's Solved these Questions
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Solved Examples
15 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.1
25 Videos
- VECTORSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
Similar Questions
A simple pendulum of length 1 oscillates aboμt the mean position as shown in the figure. If the total energy of the pendulum is E, the velocity of the pendulum bob of mass m at point P is:

View SolutionA simple pendulum suspended from the roof off a lift oscillates with frequency υ when the lift is at rest. If the lift falls freely under gravity, its frequency of oscillation becomes
View Solution
Knowledge Check
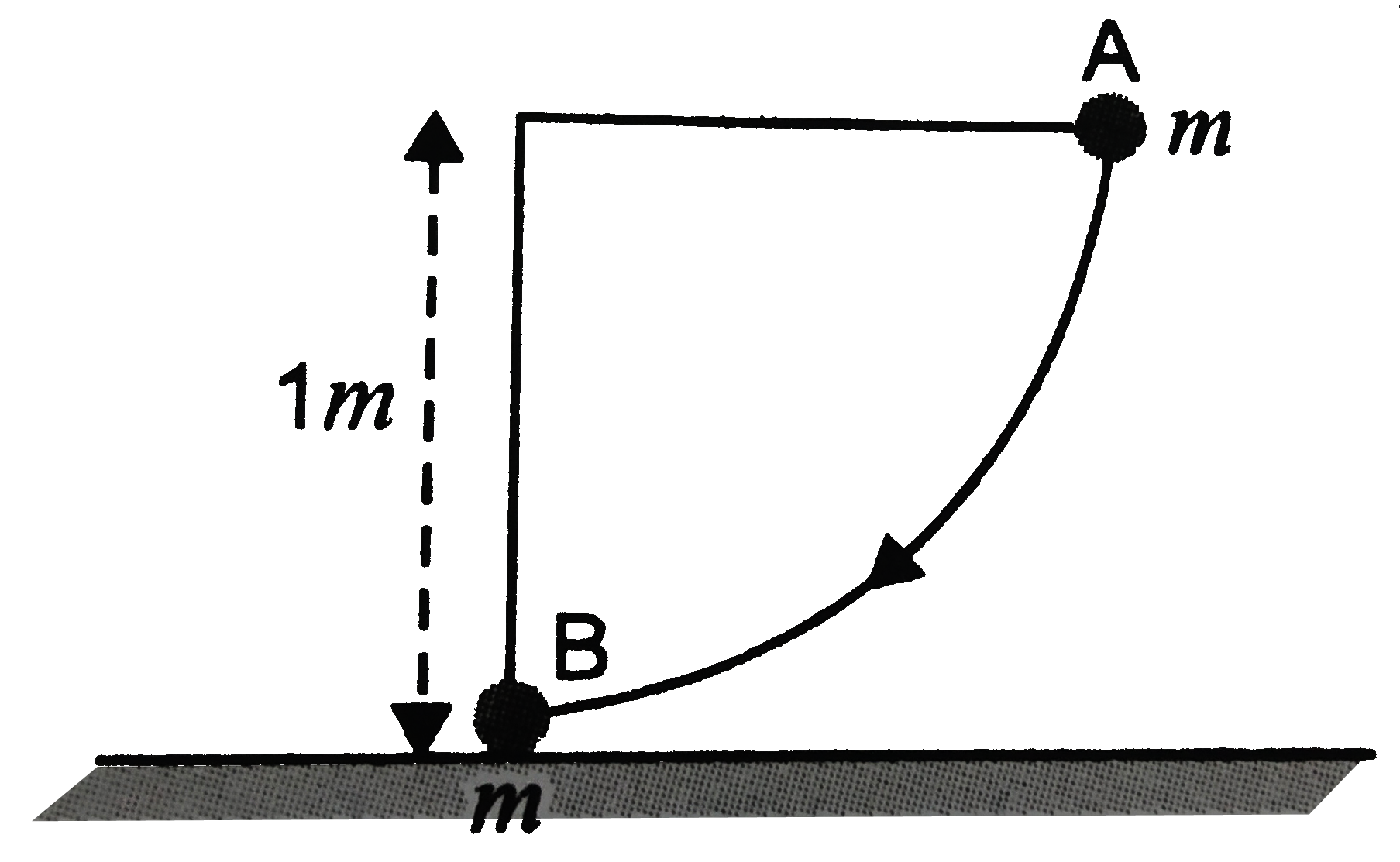
The bob A of a pendulum released from horizontal to the vertical hits another bob B of the same mass at rest on a table as shown in figure.
If the length of the pendulum is 1m, calculate
(a) the height to which bob A will rise after collision.
(b) the speed with which bob B starts moving.
Neglect the size of the bobs and assume the collision to be elastic.
 A4.47ms−1B5.47ms−1C6.47ms−1D3.47ms−1
A4.47ms−1B5.47ms−1C6.47ms−1D3.47ms−1
The figure below shows a simple pendulum of mass 200 g. It is displaced from the mean position A to the extreme position B. The potential energy at the position A is zero. At the position B the pendulum bob is raised by 5 m.
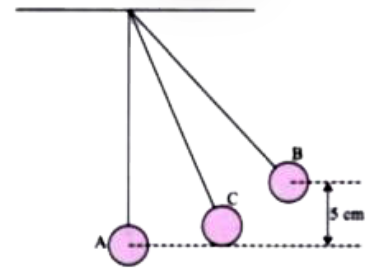
(i) What is the potential energy of the pendulum at the position B?
(ii) What is the total mechanical energy at point C?
(iii) What is the speed of the bob at the position A when released from B ?
(Take g = 10ms−2 and there is no loss of energy.)
View SolutionThe bob A of a pendulum released from horizontal to the vertical hits another bob B of the same mass at rest on a table as shown in figure.
If the length of the pendulum is 1m, calculate
(a) the height to which bob A will rise after collision.
(b) the speed with which bob B starts moving.
Neglect the size of the bobs and assume the collision to be elastic.

View SolutionA simple pendulum of length l has maximum angular displacement θ . Then maximum kinetic energy of a bob of mass m is
View SolutionA pendulum with bob of mass is scillating on either side from its resting position A between the extremes B and Cala vertical height above A. What is the kinetic energy K and potential energy U when the pendulum is al positions (i) A. (ii) B. and (in C?
View SolutionA simple pendulum of length l has a maximum angular displacement θ. The maximum kinetic energy of the bob of mass m will be
View SolutionA simple pendulum of mass m and length L is held in horizontal position. If it is released from this position, then find the angular momentum of the bob about the point of suspension when it is vertically below the point of suspension.
View SolutionFig. show a conical pendulum. If the length of the pendulum is l, mass of die bob is m and θ is the angle made by the string with the vertical show that the angular momentum of the pendulum about the point of support is:
L=√m2gl3sin4θcosθ
View Solution
