A simple pendulum of length l has a maximum angular displacement θ. The maximum kinetic energy of the bob of mass m will be
mgl(1−cosθ)
mglcosθ
mglsinθ
None of these
The correct Answer is:A
To find the maximum kinetic energy of a simple pendulum of length l with a maximum angular displacement θ, we can follow these steps:
1. Understand the Energy Conservation Principle:
The total mechanical energy in a pendulum system is conserved when only conservative forces (like gravity) are acting. This means that the sum of potential energy (PE) and kinetic energy (KE) at one position will equal the sum at another position.
2. Identify the Positions:
Let's denote the lowest point of the pendulum swing as position A (where kinetic energy is maximum) and the highest point of the swing as position B (where kinetic energy is zero).
3. Potential Energy at Position B:
At the highest point (position B), the pendulum has maximum potential energy and zero kinetic energy. The height h from the lowest point to the highest point can be calculated using the length of the pendulum l and the angle θ:
h=l−lcosθ=l(1−cosθ)
4. Calculate Potential Energy at Position B:
The potential energy at position B can be expressed as:
PEB=mgh=mg(l(1−cosθ))
5. Kinetic Energy at Position A:
At the lowest point (position A), all the potential energy has been converted into kinetic energy. Therefore, the maximum kinetic energy KEmax at position A is equal to the potential energy at position B:
KEmax=PEB=mg(l(1−cosθ))
6. Final Expression for Maximum Kinetic Energy:
Thus, the maximum kinetic energy of the bob of mass m is given by:
KEmax=mgl(1−cosθ)
Conclusion:
The maximum kinetic energy of the bob of mass m in a simple pendulum of length l with a maximum angular displacement θ is:
KEmax=mgl(1−cosθ)
The total mechanical energy in a pendulum system is conserved when only conservative forces (like gravity) are acting. This means that the sum of potential energy (PE) and kinetic energy (KE) at one position will equal the sum at another position.
Let's denote the lowest point of the pendulum swing as position A (where kinetic energy is maximum) and the highest point of the swing as position B (where kinetic energy is zero).
At the highest point (position B), the pendulum has maximum potential energy and zero kinetic energy. The height h from the lowest point to the highest point can be calculated using the length of the pendulum l and the angle θ:
h=l−lcosθ=l(1−cosθ)
The potential energy at position B can be expressed as:
PEB=mgh=mg(l(1−cosθ))
At the lowest point (position A), all the potential energy has been converted into kinetic energy. Therefore, the maximum kinetic energy KEmax at position A is equal to the potential energy at position B:
KEmax=PEB=mg(l(1−cosθ))
Thus, the maximum kinetic energy of the bob of mass m is given by:
KEmax=mgl(1−cosθ)
The maximum kinetic energy of the bob of mass m in a simple pendulum of length l with a maximum angular displacement θ is:
KEmax=mgl(1−cosθ)
Topper's Solved these Questions
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Match the columns
3 Videos
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Medical entrances s gallery
19 Videos
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Check point
45 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Subjective
21 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Only One Option is Correct
27 Videos
Similar Questions
A simple pendulum of length l has maximum angular displacement θ . Then maximum kinetic energy of a bob of mass m is
View SolutionThe bob of a simple pendulum of length L is released at time t = 0 from a position of small angular displacement θ0 . Its linear displacement at time t is given by :
View Solution
Knowledge Check
Assertion: The motion of a simple pendulum is simple harmoni for all angular displacement.
Reason: Motion of simple pendulum is independent of the angular displacement.AIf both assertion and reson are true and reason is the correct explanation of assertionBIf both assertion and reason are true but reason is not the correct explanation of assertion.CIf assertion is true but reason is false.DIf both assertion and reason are false.
A simple pendulum of mass 'm' , swings with maximum angular displacement of 60∘ . When its angular displacement is 30∘ ,the tension in the string is
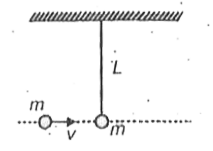
View SolutionA small ball of mass m moving with speed v (>√2gL) undergoes an elastic head on collision with a stationary bon of identical mass of a simple pendulum of length L. The maximum height h, from the equilibrium position, to which the bob rises after collision is
View SolutionA simple pendulum of length l swimings from a small angle θ . Its swinging is constrained by the smooth inclined planes OP and PC. Assuming elastic collision of the bob with the plane PC, find
angular amplitude for the motion of the bob in the left hand side of its mean possition.
.

View SolutionA pendulum is executing simple harmonic motion and its maximum kinetic energy is K1. If the length of the pendulum is doubled and it perfoms simple harmonuc motion with the same amplitude as in the first case, its maximum kinetic energy is K2 Then:
View SolutionThe diagram below shows a pendulum having a bob of mass 80 g. A and C are extreme positions and B is the mean position. The bob has velocity 5m/s at position B. Assuming there is no loss of energy, select the correct statements from the options given below: [ g = 10 N/kg ]
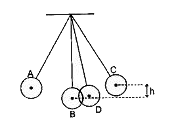
At point A the bob will have only kinetic energy.
The maximum potential energy gained by the bob will be 1000J.
The maximum height 'h' reached by the bob will be 125 cm.
At point D the bob will have maximum kinetic energy.
The maximum potential energy gained by the bob will be 1 J
At point B the energy possessed by the bob is 1000 J.
View SolutionA simple pendulum is oscillating with angular displacement 90∘ For what angle with vertical the acceleration of bob direction horizontal?
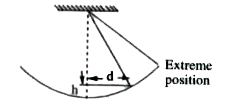
View SolutionA simple pendulum of length 1 oscillates aboμt the mean position as shown in the figure. If the total energy of the pendulum is E, the velocity of the pendulum bob of mass m at point P is:
View Solution
