Which of the following circuits gives the correct value of resistance, when computed by using R=(V/I) where V and I are voltmeter and ammeter reading, respectively? The meters are not ideal.
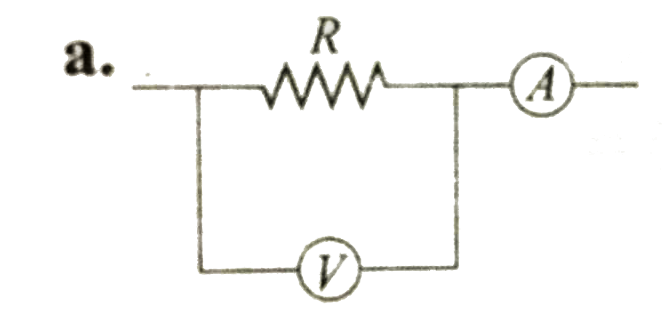
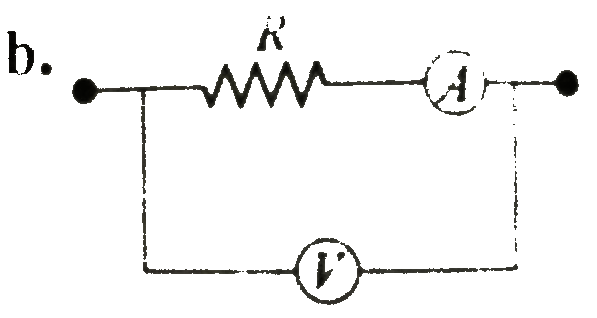
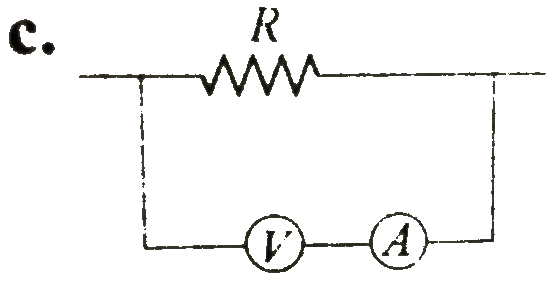
none of these
The correct Answer is:D
To solve the problem of determining which circuit gives the correct value of resistance using the formula R=VI, where V is the voltmeter reading and I is the ammeter reading, we need to analyze the behavior of the ammeter and voltmeter in different circuit configurations.
1. Understand the Concept:
- The formula R=VI gives the correct resistance value only if V is the potential difference across the resistor and I is the current flowing through that same resistor.
2. Consider Non-Ideal Meters:
- Since the meters are not ideal, they have finite resistances. Let Ra be the resistance of the ammeter and Rv be the resistance of the voltmeter. This means that both meters will affect the circuit operation.
3. Analyze Circuit Cases:
- Case 1: If the voltmeter is connected in parallel with the resistor:
- The voltmeter will draw some current I′ due to its resistance Rv.
- The current flowing through the resistor will then be I−I′ (where I is the total current).
- The voltmeter will read the voltage across both the resistor and its own resistance, which will not give the correct voltage across the resistor alone.
- Thus, R=VI will not yield the correct resistance.
- Case 2: If the ammeter is connected in series with the resistor:
- The ammeter will read the total current I flowing through the circuit.
- However, the voltmeter will measure the voltage drop across both the resistor and the ammeter's resistance Ra.
- Therefore, the voltmeter reading V will not be the voltage across the resistor alone, leading to R=VI not giving the correct resistance.
- Case 3: If the ammeter is connected in parallel with the resistor:
- The ammeter will not measure the current flowing through the resistor, as it is bypassed.
- This configuration is incorrect for measuring resistance since the ammeter will read a different current than what flows through the resistor.
4. Conclusion:
- In all analyzed cases, the configurations do not yield the correct resistance value when using R=VI due to the non-ideal nature of the meters and their placements in the circuit.
- Therefore, the answer is that none of the circuits provide the correct value of resistance.
- The formula R=VI gives the correct resistance value only if V is the potential difference across the resistor and I is the current flowing through that same resistor.
- Since the meters are not ideal, they have finite resistances. Let Ra be the resistance of the ammeter and Rv be the resistance of the voltmeter. This means that both meters will affect the circuit operation.
- Case 1: If the voltmeter is connected in parallel with the resistor:
- The voltmeter will draw some current I′ due to its resistance Rv.
- The current flowing through the resistor will then be I−I′ (where I is the total current).
- The voltmeter will read the voltage across both the resistor and its own resistance, which will not give the correct voltage across the resistor alone.
- Thus, R=VI will not yield the correct resistance.
- The ammeter will read the total current I flowing through the circuit.
- However, the voltmeter will measure the voltage drop across both the resistor and the ammeter's resistance Ra.
- Therefore, the voltmeter reading V will not be the voltage across the resistor alone, leading to R=VI not giving the correct resistance.
- The ammeter will not measure the current flowing through the resistor, as it is bypassed.
- This configuration is incorrect for measuring resistance since the ammeter will read a different current than what flows through the resistor.
- In all analyzed cases, the configurations do not yield the correct resistance value when using R=VI due to the non-ideal nature of the meters and their placements in the circuit.
- Therefore, the answer is that none of the circuits provide the correct value of resistance.
Similar Questions
In the series L-C-R circuit , the voltmeter and ammeter readings are respectively
 View Solution
View SolutionIn the circuit shown the reading of ammeter and voltmeter are 4A and 20V respectively. The meters are non ideal, then R ia
 View Solution
View SolutionThe value of resistance of an unknown resistor is calculated using the formula R=V/I where V and I are the readings of the voltmeter and the ammeter, respectivley. Consider the circuits below. The internal resistances of the voltmeter and the ammeter (RVandRG,respectively) are finite and nonzero.
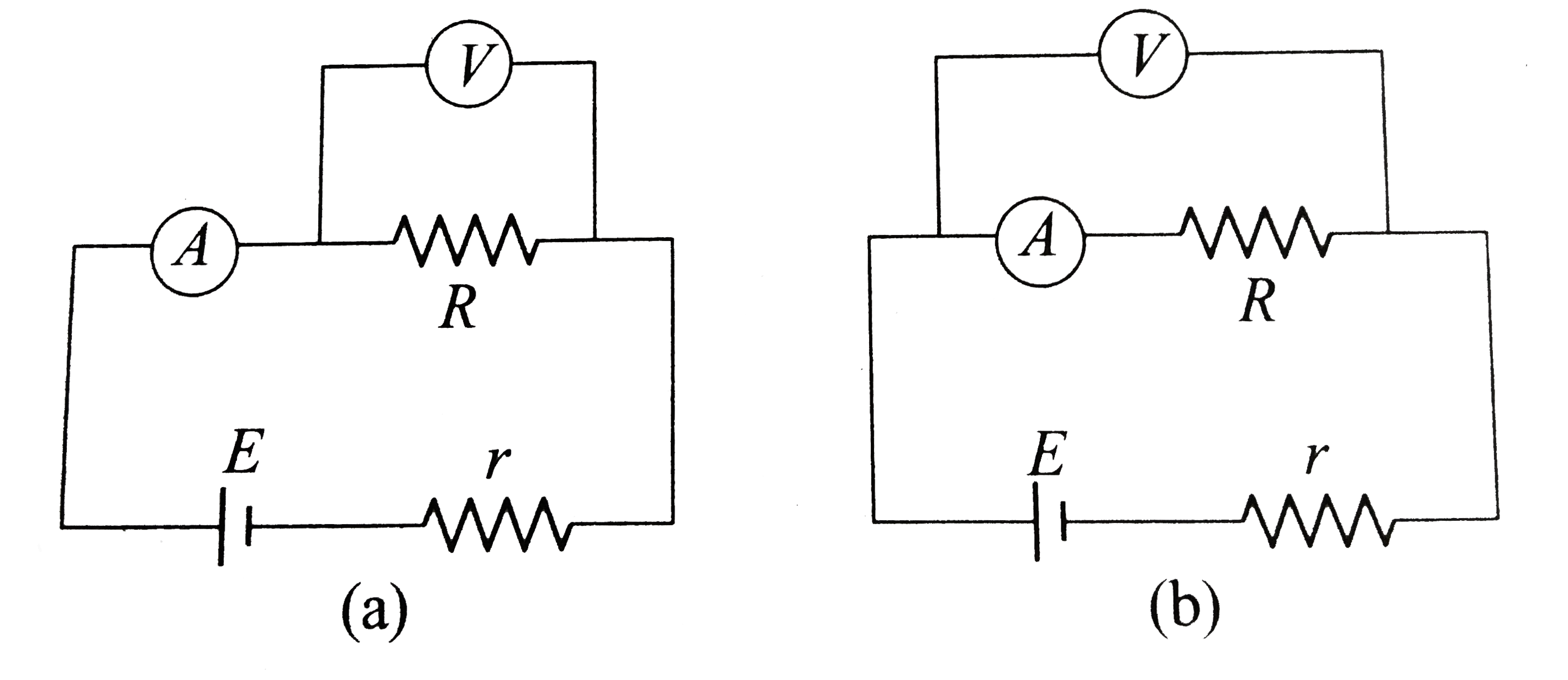 ,
,
Let RAandRB be the calculated values in the two cases A and B , respectively.
If the resistance of voltmeter is RV=1kΩ and the percentage error in the measurement of R (the value of R is nearly 10Ω)isView SolutionIn the circuit shown in figure neglecting source resistance, the voltmeter and ammeter reading will respectively be
 View Solution
View SolutionIn the circuit shown in figure neglecting source resistance the voltmeter and ammeter reading will respectively, will be
 View Solution
View SolutionThe actual value of resistance R, shown in the figure is 30Ω. This is measured in an experiment as shown using the standard formula R=VI, where V and I are the readings of the voltmeter and ammeter, respectively. If the measured value of R is 5% less, then the internal resistance of the voltmeter is
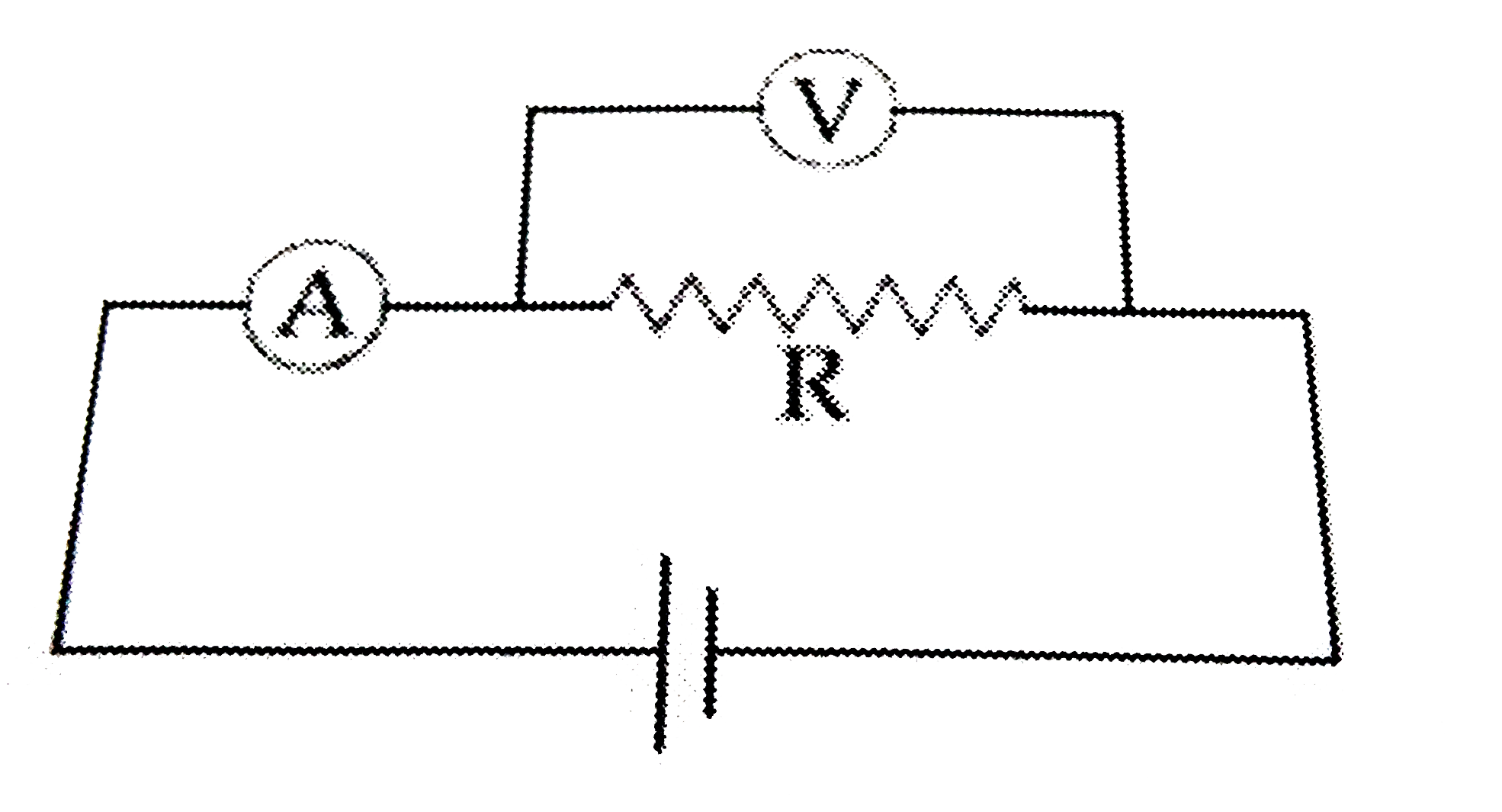 View Solution
View SolutionIn the circuit shown, A and V are ideal ammeter and voltmeter respectively. Reading of the voltmeter will be
 View Solution
View SolutionIn the following circuit, determine the reading of ideal voltmeter (V) and ideal ammeter (A).
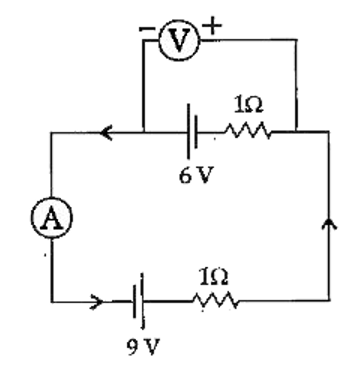 View Solution
View SolutionIn the circuit figure, the voltmeter reads 30 V. The resistance of the voltmeter is
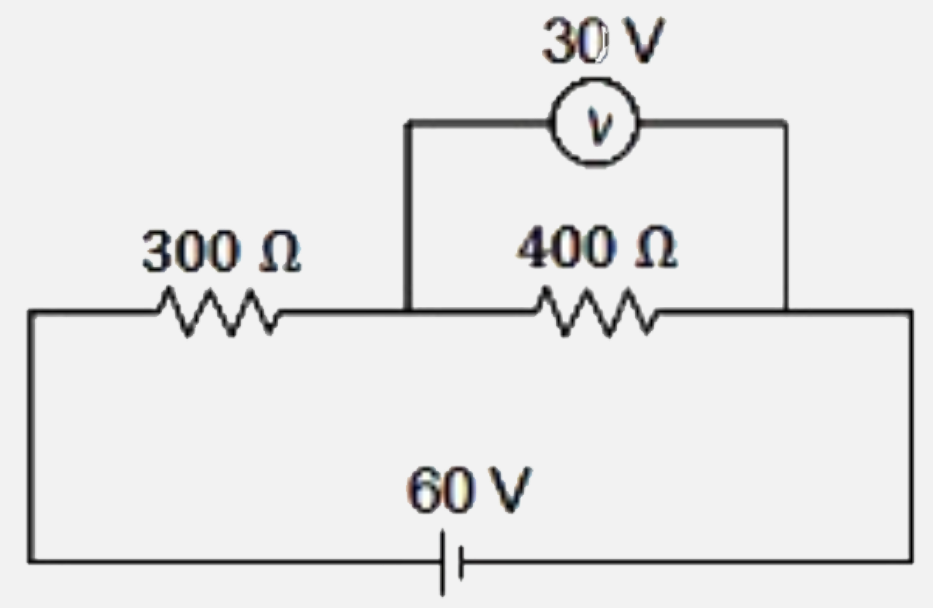 View Solution
View SolutionThe reading of ammeter and voltmeter in the following circuit are respectively
 View Solution
View Solution

