A total charge Q flows across a resistor R during a time interval T in such a way that the current versus time graph for 0 to T is like the loop of a sine curve in the range 0toπ. The total heat generated in the resistor is
Q2π2R/8T
2Q2π2R/T
Q2π2R/T
Q2π2R/2T
The correct Answer is:A
To find the total heat generated in the resistor when a total charge Q flows across it during a time interval T, we can follow these steps:
Step 1: Understand the Current Function
The current I(t) is given by the equation of a sine wave:
I(t)=I0sin(πtT)
where I0 is the maximum current.
Step 2: Relate Charge and Current
The total charge Q that flows through the resistor can be expressed as:
Q=∫T0I(t)dt
Substituting the expression for I(t):
Q=∫T0I0sin(πtT)dt
Step 3: Calculate the Integral
To solve the integral:
Q=I0∫T0sin(πtT)dt
Using the substitution u=πtT gives dt=Tπdu. The limits change from 0 to π:
Q=I0⋅Tπ∫π0sin(u)du
The integral of sin(u) from 0 to π is 2:
Q=I0⋅Tπ⋅2=2I0Tπ
Step 4: Solve for I0
Rearranging gives:
I0=Qπ2T
Step 5: Calculate the Heat Generated
The heat H generated in the resistor can be calculated using:
H=∫T0I2(t)Rdt
Substituting I(t):
H=R∫T0(I0sin(πtT))2dt
This simplifies to:
H=RI20∫T0sin2(πtT)dt
Step 6: Evaluate the Integral
Using the identity sin2(x)=1−cos(2x)2:
H=RI20⋅T2(1−12∫T0cos(2πtT)dt)
The integral of cos(2πtT) over one complete cycle is zero:
H=RI20⋅T2
Step 7: Substitute I0
Substituting I0=Qπ2T:
H=R(Qπ2T)2⋅T2
This simplifies to:
H=R⋅Q2π24T2⋅T2=Q2π2R8T
Final Answer
The total heat generated in the resistor is:
H=Q2π2R8T
The current I(t) is given by the equation of a sine wave:
I(t)=I0sin(πtT)
where I0 is the maximum current.
The total charge Q that flows through the resistor can be expressed as:
Q=∫T0I(t)dt
Substituting the expression for I(t):
Q=∫T0I0sin(πtT)dt
To solve the integral:
Q=I0∫T0sin(πtT)dt
Using the substitution u=πtT gives dt=Tπdu. The limits change from 0 to π:
Q=I0⋅Tπ∫π0sin(u)du
The integral of sin(u) from 0 to π is 2:
Q=I0⋅Tπ⋅2=2I0Tπ
Rearranging gives:
I0=Qπ2T
The heat H generated in the resistor can be calculated using:
H=∫T0I2(t)Rdt
Substituting I(t):
H=R∫T0(I0sin(πtT))2dt
This simplifies to:
H=RI20∫T0sin2(πtT)dt
Using the identity sin2(x)=1−cos(2x)2:
H=RI20⋅T2(1−12∫T0cos(2πtT)dt)
The integral of cos(2πtT) over one complete cycle is zero:
H=RI20⋅T2
Substituting I0=Qπ2T:
H=R(Qπ2T)2⋅T2
This simplifies to:
H=R⋅Q2π24T2⋅T2=Q2π2R8T
The total heat generated in the resistor is:
H=Q2π2R8T
Similar Questions
Knowledge Check
The charge flowing through a resistance R varies with time t as Q=at−bt2. The total heat produced in R is
Aa3RbBa3R2bCa3R3bDa3R6b
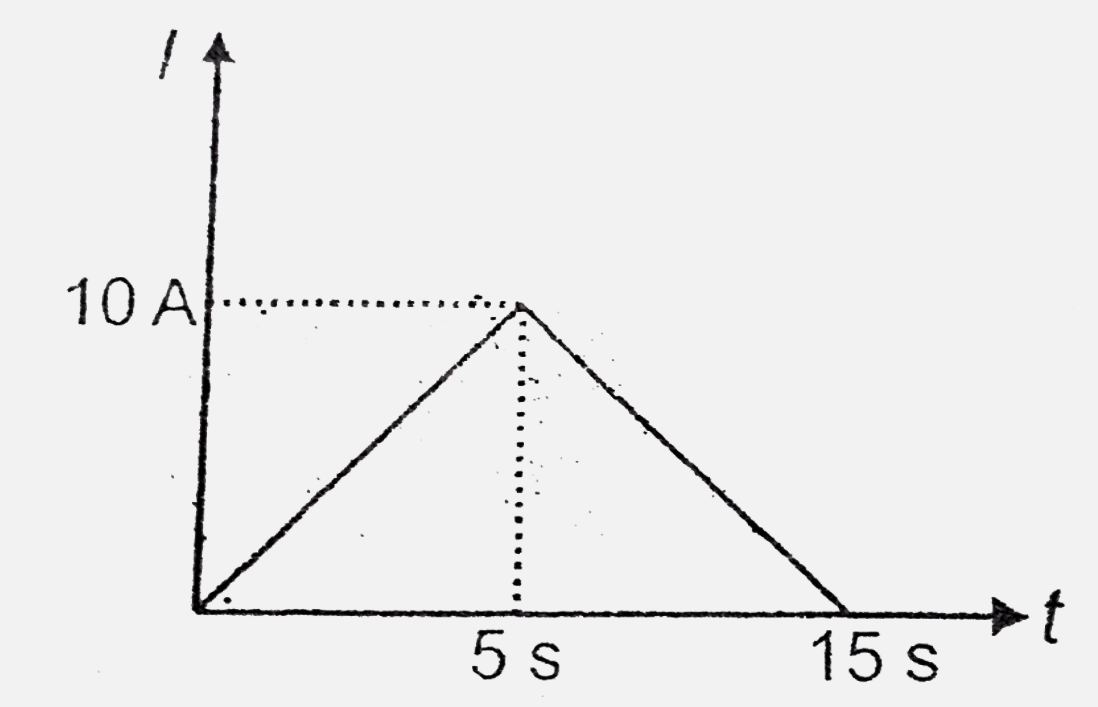
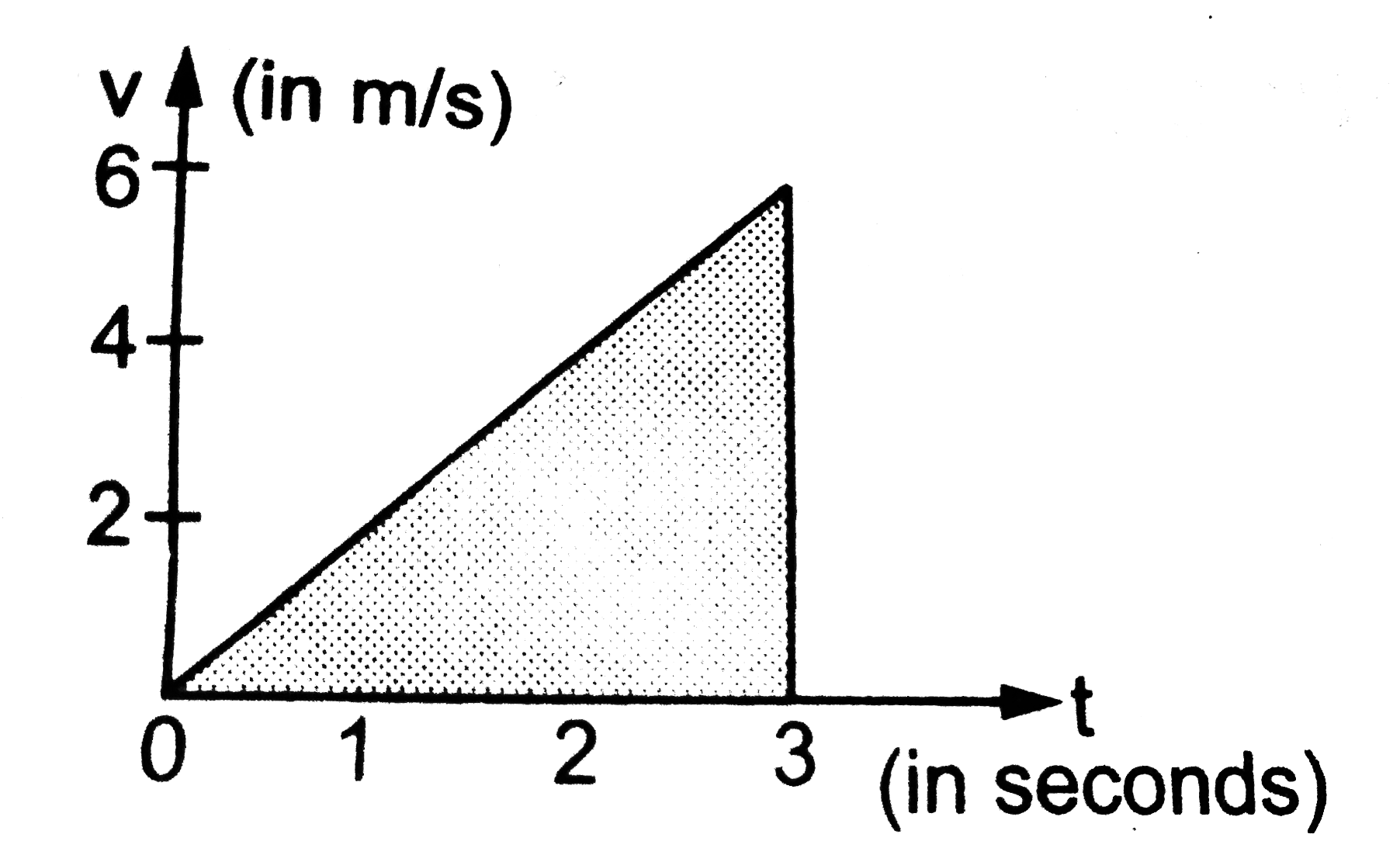
Figure shows the speed versus time graph for a particle. Find the distance travelled by the particle during the time t=0 to t=3s.
View SolutionCurrent passing through a resistor of resistance 5Ω varies with time as shown in the graph.Heat generated in the resistance during 3s is equal to
_PHY_E05_283_Q01.png)
View SolutionA magnetic flux through a stationary loop with a resistance R varies during the time interval τ as ϕ=at(τ−t). Find the amount of heat the generated in the loop during that time
View SolutionThe total heat produced in resistor r in an RL circuit when the current in the inductor decreases from Io to 0 is
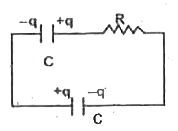
View SolutionTwo capacitors, having equal capacitance C, are having same charges q on each plate. They are connected across a resistor R as shown in the figure. What is the total heat generated in the resistor upto the instant when the steady state has reached
View SolutionThe potentiak difference across a 2H inductor as a function of time is shown in the figure. At time t=0, current is zero.

Current versus time graph across the inductor will be
View Solution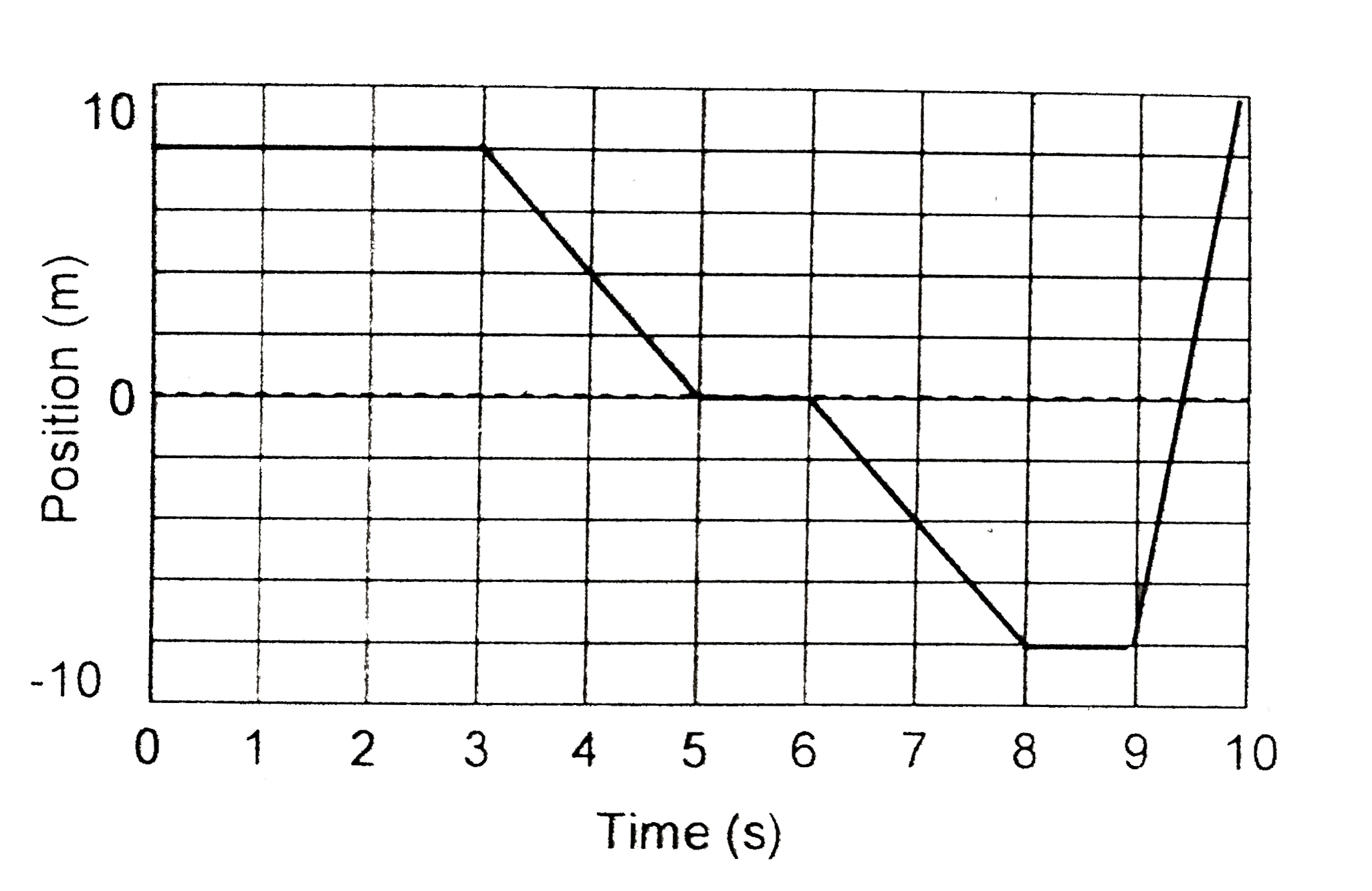
The position versus time graph of a particle moving along a straight line is shown. What is the total distance travelled by the particle from t=0s to t=10s?
View Solution