This question concerns a symmetrical lens shown, along with its two focal points. It is made of plastic with n=1.2 and has focal length f. Four different regions are shown:
A. −∞<x<−f
B. −f<x<0
C. 0<x<f
D. f<x<∞
A second lens is now placed adjacent to the first in contact with it. The new lens is concave, with a focal length f=−3f. In what region does the focal length of the two-lens system lie? Treat the lenses as thin.
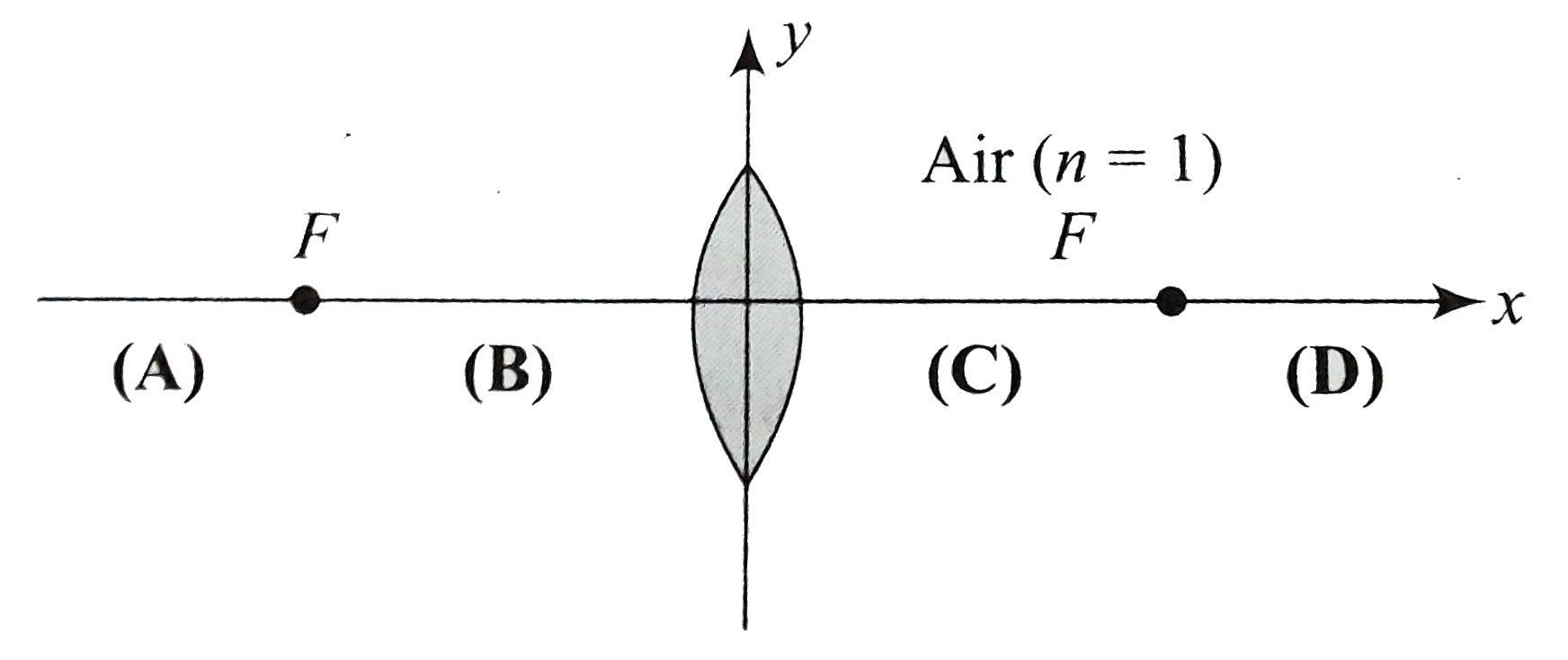
A
B
C
D
The correct Answer is:d
From the formula of equivalent focal length of thin lenses in contact, we get
1F=1f1+1f2=1f−13forF=3f2
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Integer15videos
GEOMETRICAL OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Archives7videos
GEOMETRICAL OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Assertion-Reasoninig2videos
GEOMETRICAL OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSEXERCISE - dpp 3.315videos
ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Thermal Power in Resistance Connected in Circuit27videos
HEATING EFFECT OF CURRENT
Similar Questions
This question concerna a symmetrical lens shown, along with its two focal points. It is made of plastice with n=1.2 and has focal length f. Four different regions are shown:
Here,
A. −∞x<−f B. −f<x<0
C. 0<x<f D. f<x<∞
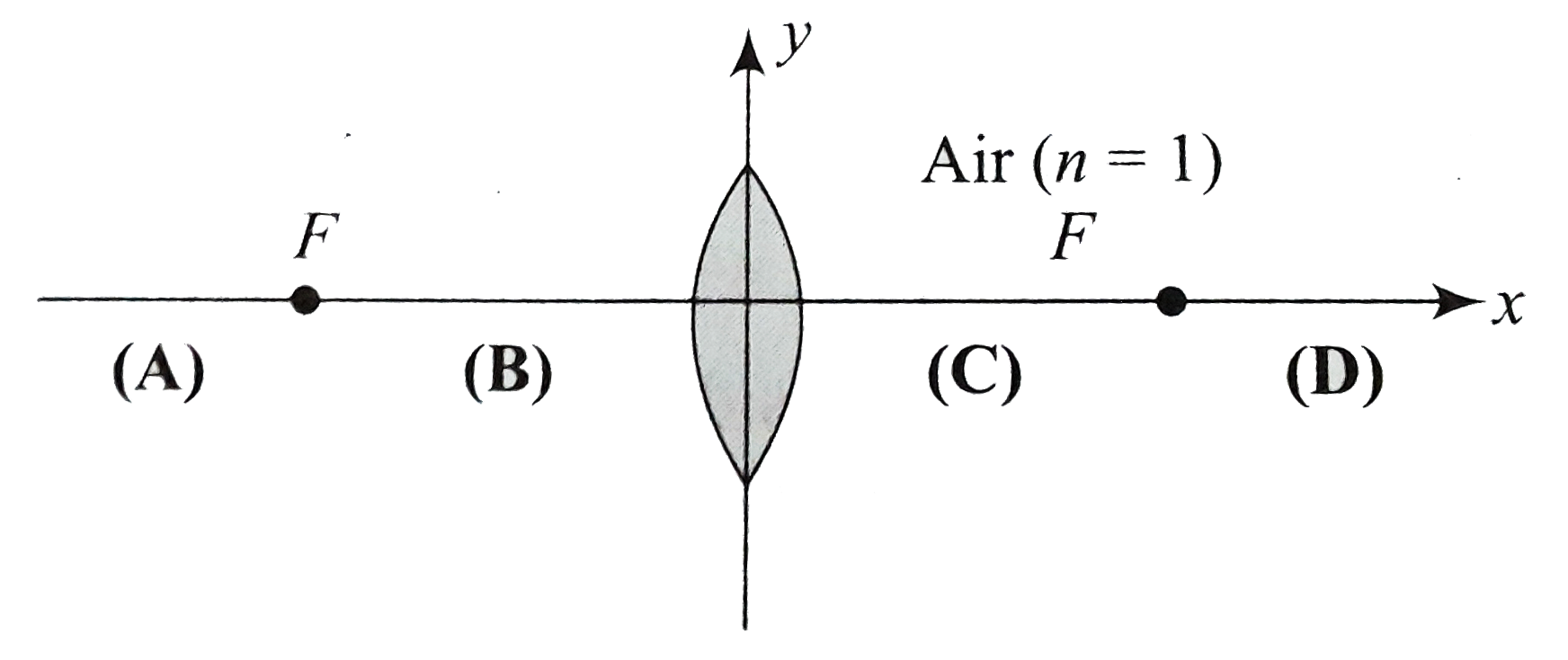
Q. If incident rays are converging, then in which region does the image appear?View SolutionThe order of energy of orbitals is s<p<d<f
View SolutionFind the inverse of each of the following functions :
f(x)=⎧⎪⎨⎪⎩x,−∞<x<1x2,1≤x≤42x,4<x<∞View SolutionIdentify the null sets among the following
F = {x : x ∈N,5<x<6.}View SolutionIf E and F are independent events such that 0<P(E)<1and 0<P(F)<1, then
View SolutionLet f(x)={2−x,−3≤x≤0x−2,0<x<4 Then f−1 (x) is discontinous at x=
View SolutionFind df/dx if f(x) = (sin x) ^ sin x for all o<x<π.
View SolutionThe number of points at which f(x)=[x]+|1−x|,−1<x<3 is not differentiable is (where [.] denotes G.I.F)
View SolutionLet f(x)={a−3x−2≤x<04x±30≤x<1,iff(x) has smallest valueat x=0, then range of a, is
View SolutionThe function f(x)={x2a , if 0≤x<1 a , if 1≤x is continuous then find the value of constant term
View Solution

