A thin biconvex lens of refractive index 3/2 is placed on a horizontal plane mirror as shown in Figure . The space between the lens and the mirror is then fille with water or refractive index 4/3. It is found that when a point object is placed 15 cm above the lens on its principal axis, the object coincides with its own image. On representing with another liquid, the object and the image again coincide at a distance 25 cm from the lens. Calculate the refractive index of the liquid.

1.6
2.6
2.8
3.2
The correct Answer is:a.
The light retraced its path if it is incident normally on a mirror. The ray after refraction through the lens and the liquid are parallel. We will apply the general thin lens equation with parameters.
n1=1,n2=3/2,n3=4/3,u=−15cm,andυ=∞
n3υ−n1u=(n2−n1)R+(n3−n2R)
n3∞−1(−15)=(3/2)−1R−[(4/3)−(3/2)]R
On solving for R, we get R=10cm. Similarly, when second liquid is filled, we have
n′3∞−1(−25)=(3/2)−110−n′3−(3/2)10
On solving for n′3 , we get, n′3=1.6
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Integer15videos
GEOMETRICAL OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Archives7videos
GEOMETRICAL OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Assertion-Reasoninig2videos
GEOMETRICAL OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSEXERCISE - dpp 3.315videos
ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Thermal Power in Resistance Connected in Circuit27videos
HEATING EFFECT OF CURRENT
Similar Questions
A thin equiconvex lens of refractive index 3/2 is placed on a horizontal plane mirror as shown in figure. The space between the lens and the mirror is filled with a liquid of refractive index 4/3 . It is found that when a point object is placed 15 cm above the lens on its priincipal axis, the object coincides with its own image.

Q. If another liquid is filled instead of water, the object and the image coincide at a distance 25 cm from the lens.
Calculate the refractive index of the liquid.View SolutionA thin equiconvex lens of refractive index 3/2 is placed on a horizontal plane mirror as shown in figure. The space between the lens and the mirror is filled with a liquid of refractive index 4/3 . It is found that when a point object is placed 15 cm above the lens on its priincipal axis, the object coincides with its own image.

Q. The radius of curvature of the convex surface isView Solution
Knowledge Check
- Question 1 - Select One
A convex lens of focal length 15 cm is placed on a plane mirror. An object is placed at 30 cm from the lens. The image is
Areal, at 30 cm in front of the mirrorBreal, at 30 cm behind the mirrorCreal, at 10 cm in front of the mirrorDvirtual, at 10 cm behind the mirror
An equiconvex lens of refractive index n2 is placed such that the refractive index of the surrouding media is as shown. The lens :
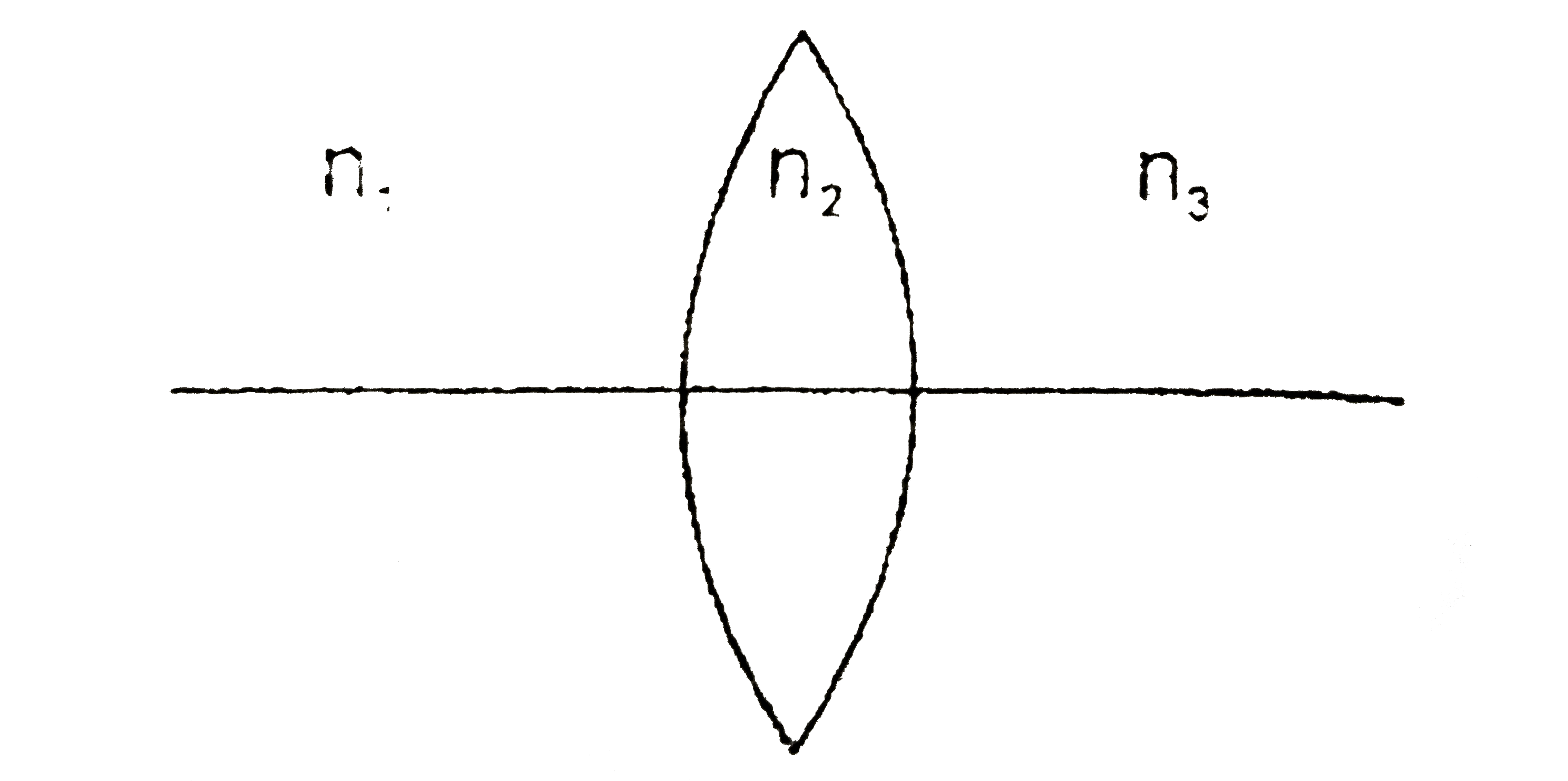 View Solution
View SolutionA thin bi-convex lens made up of glass of refractive index 3/2 is placed is front of a plane mirror. The space between the lens and the mirror is filled with water of refractive index 4/3 . The radii of curvatures of the lens are R1=15cm and R2=25cm . A point object is placed at distance x from the surface whose curvature is R1. The distance x is greater than the separation between the lens and the mirror. Find the value of x so that image must coincide with the object.
View SolutionA biconvex lens of focal length 15cm is in front of a plane mirror. The distance between the lens and the mirror is 10cm. A small object is kept at distance of 30cm from the lens. The final image is
View SolutionOn a horizontal plane mirror, a thin equiconvex lens of glass is placed and when the space between the lens and mirror is filled with a liquid, an object held at a distance D which is 30cm vertically above the lens is found to coincide with its own image as shown in Figure. If equiconvex lens of glass has refractive index μ=1.5 and radius of curvature R=20cm then find refractive index of the liquid.
 View Solution
View SolutionA thin convex lens of focal length 30cm is placed in front of a plane mirror. An object is placed at a distance x from the lens (not in between lens and mirror ) so that its final image coincides with itself. Then, the value of x is
View SolutionA small object is kept at 18cm from combination of a convex lens and plane mirror to get the image on object itself. Now the space between lens and mirror is filled with liquid of refractive index μL. Now we need to keep the object at 27cm to get the image on object. Find μL.
_2019_CBT4_E01_078_Q01.png) View Solution
View SolutionA thin lens of focal length +10.0cm lies on a horizontal plane mirror. How far above the lens should an object be be held if its image is to coincide with the object?
View Solution

