White light may be considered to be mixture of waves of λ ranging between 3900Å and 7800Å. An oil film of thickness 10,000Å is examined normally by the reflected light. If μ=1.4, then the film appears bright for
4308Å, 5091Å,6222Å
4000Å,5091Å,5600Å
4667Å,6222Å,7000Å
4000Å,4667Å,5600Å,7000Å
The correct Answer is:A
To determine the wavelengths for which the oil film appears bright, we will use the condition for constructive interference in thin films. Here’s a step-by-step solution:
Step 1: Understanding the Condition for Constructive Interference
For constructive interference in a thin film, the condition is given by:
2μt=(n+12)λ
where:
- μ is the refractive index of the film,
- t is the thickness of the film,
- n is the order of interference (0, 1, 2, ...),
- λ is the wavelength of light in vacuum.
Step 2: Rearranging the Formula
We can rearrange the formula to solve for λ:
λ=2μtn+12
Step 3: Substituting Known Values
Given:
- μ=1.4
- t=10,000Å=10,000×10−10m=10−6m
Now substituting these values into the equation:
λ=2×1.4×10,000n+12
λ=28,000n+12
Step 4: Finding Wavelengths for Different Orders of Interference
Now we will calculate λ for different values of n:
1. For n=0:
λ=28,0000+12=28,0000.5=56,000Å
2. For n=1:
λ=28,0001+12=28,0001.5≈18,667Å
3. For n=2:
λ=28,0002+12=28,0002.5=11,200Å
4. For n=3:
λ=28,0003+12=28,0003.5≈8,000Å
5. For n=4:
λ=28,0004+12=28,0004.5≈6,222Å
6. For n=5:
λ=28,0005+12=28,0005.5≈5,091Å
7. For n=6:
λ=28,0006+12=28,0006.5≈4,307Å
Step 5: Identifying Valid Wavelengths
The wavelengths calculated must fall within the visible spectrum of white light, which ranges from 3900Å to 7800Å. The valid wavelengths from our calculations are:
- For n=0: 56,000Å (not valid)
- For n=1: 18,667Å (not valid)
- For n=2: 11,200Å (not valid)
- For n=3: 8,000Å (not valid)
- For n=4: 6,222Å (valid)
- For n=5: 5,091Å (valid)
- For n=6: 4,307Å (valid)
Conclusion
The oil film appears bright for wavelengths 6,222Å, 5,091Å, and 4,307Å.
For constructive interference in a thin film, the condition is given by:
2μt=(n+12)λ
where:
- μ is the refractive index of the film,
- t is the thickness of the film,
- n is the order of interference (0, 1, 2, ...),
- λ is the wavelength of light in vacuum.
We can rearrange the formula to solve for λ:
λ=2μtn+12
Given:
- μ=1.4
- t=10,000Å=10,000×10−10m=10−6m
λ=2×1.4×10,000n+12
λ=28,000n+12
Now we will calculate λ for different values of n:
λ=28,0000+12=28,0000.5=56,000Å
λ=28,0001+12=28,0001.5≈18,667Å
λ=28,0002+12=28,0002.5=11,200Å
λ=28,0003+12=28,0003.5≈8,000Å
λ=28,0004+12=28,0004.5≈6,222Å
λ=28,0005+12=28,0005.5≈5,091Å
λ=28,0006+12=28,0006.5≈4,307Å
The wavelengths calculated must fall within the visible spectrum of white light, which ranges from 3900Å to 7800Å. The valid wavelengths from our calculations are:
- For n=0: 56,000Å (not valid)
- For n=1: 18,667Å (not valid)
- For n=2: 11,200Å (not valid)
- For n=3: 8,000Å (not valid)
- For n=4: 6,222Å (valid)
- For n=5: 5,091Å (valid)
- For n=6: 4,307Å (valid)
The oil film appears bright for wavelengths 6,222Å, 5,091Å, and 4,307Å.
Similar Questions
A light of wavelength 5890Å falls normally on a thin air film. The minimum thickness of the film such that the film appears dark in reflected light is
View SolutionA parallel beam of white light is incident on a thin film of air of uniform thickness. Wavlength 7200Å and 5400Å are observed to be missing from the spectrum of reflected light viewed normally. The other wavelength in the visible region missing in the reflected spectrum is
View SolutionWhen white light is incident normally an oil film of thickness 10−4cm and refractive index. 1.4 then the wavelength which will not be seen in the reflected system of light is
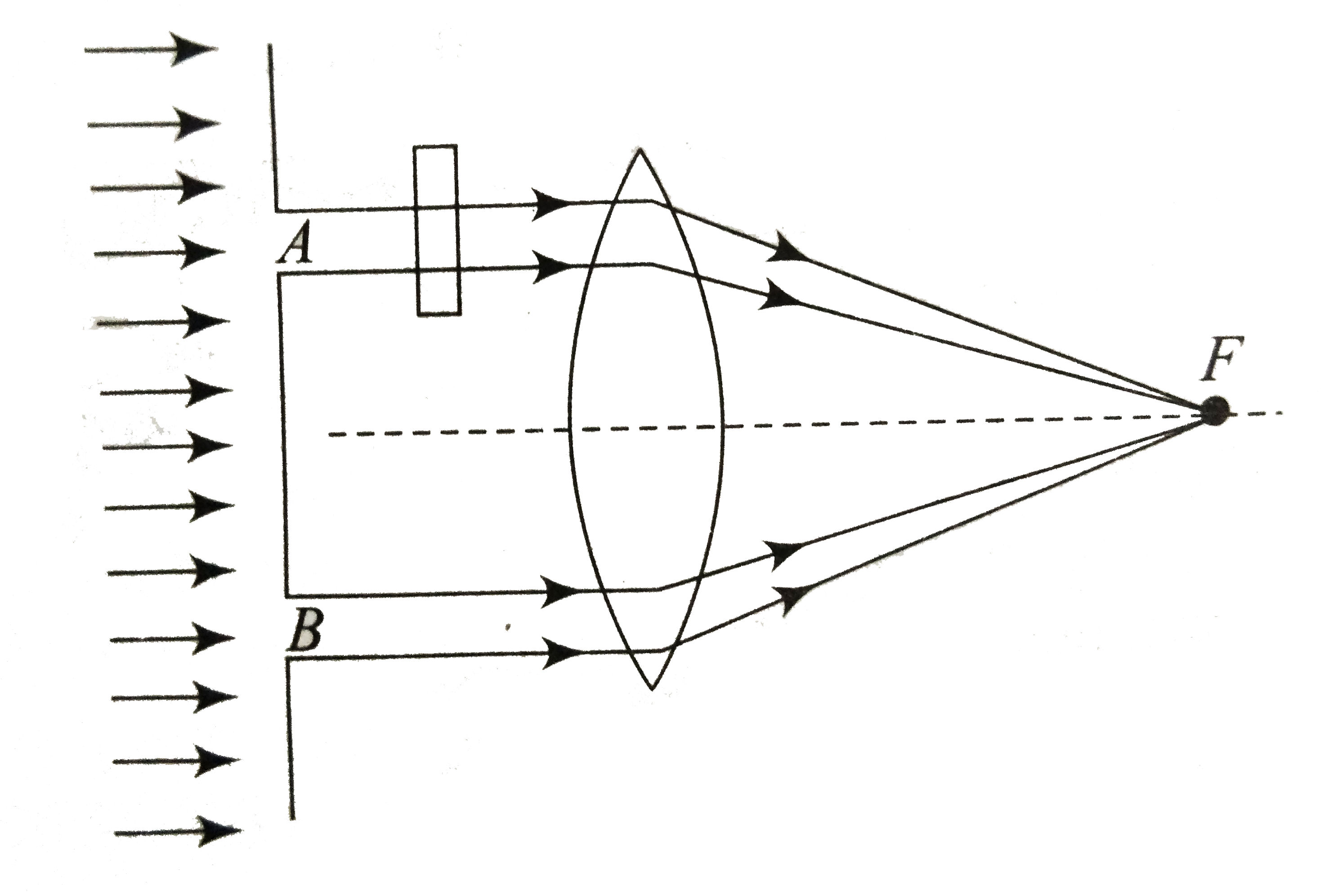
View SolutionIn a modified Young's double-slit experiment, a monochromatic uniform and parallel beam of light of wavelength 6000Å and intensity (10/π) W m−2 is incident normally on two circular apertures A and B of radii 0.001 m and 0.002 m, respectively. A perfectly transparent film of thickness 2000Å and refractive index 1.5 for the wavelength of 6000Å is placed in front of aperture A (see the figure). Calculate the power (in mW) received at the focal spot F of the lens. Then lens is symmetrically placed with respect to the aperture. Assume that 10% of the power received by each aperture goes in the original direction and is brought to the focal spot.
View SolutionWhite light reflected at normal incidence from a soap film has minima at 6500Å and maxima at 7500Å in the visible region without minimum in between. If μ is 53 for the thin film, thickness of the film is
View SolutionA plane wave of monochromatic light falls normally on a uniform thin or oil which covers a glass plate. The wavelength of source can be varied continuously. Complete destructive is observed for λ=5000Å and λ=1000Å and for no other wavelength in between. If μ of oil is 1.3 and that of glass is 1.5, the thickness of the film will be
View SolutionA thin oil film of refracting index 1.2 floats on the surface of water (μ=43). When a light of wavelength λ=9.6×10−7m falls normally on the film air, then it appears dark when seen normally. The minimum change in its thickness for which it will appear bright in normally reflected light by the same light is Z×10−7m. Then find Z.
View SolutionA light beam of wavelength 600nm in air passes through film 1(n1=1.2) of thickness 1.0μm,then through film 2(air) of thickness 1.5μm, and finally through film 3(n3=1.8) of thick≠ss1.0mu m.
(a) Which film does the light cross in the least time, and what is that least time?
(b) What are the total number of wavelength (at any instant) across all three films together?
View SolutionInterference fringes were produced in Young's double-slit experiment using light of wavelength 5000Å. When a film of thickness 2.5×10−3cm was placed in front of one of the slits, the fringe pattern shifted by a distance equal to 20 fringe-widths. The refractive index of the material of the film is
View SolutionThe outer surface of a transparent glass slab of refractive index μS=1.5 is coated by a thin layer of transparent medium of refractive index μC=1.6. Orange light of wavelength 6400Å falls normally on the coating. The reflected light at the upper surface and at the lower surface of the coat interfere destructively. If thickness of the coat is 5K×10−8m, calculate the minimum value of K.
View Solution
