In YDSE, the sources is place symmetrical to the slits. If a transparent slab is placed in front of the upper slit, then
intensity of central maxima may change
intensity of central maxima may not change
central maxima will be shifted up
intensity of dark fringe will be always zero
The correct Answer is:a.,b.,c.
To solve the problem regarding the Young's Double Slit Experiment (YDSE) with a transparent slab placed in front of the upper slit, we can break down the solution into the following steps:
1. Understanding the Setup:
- In the YDSE, we have two slits (let's call them S1 and S2) and a light source placed symmetrically to these slits. A transparent slab is placed in front of the upper slit (S1).
2. Effect of the Transparent Slab:
- The transparent slab can absorb some light, which may change the intensity of the light coming from the upper slit (S1). This absorption can affect the overall intensity of the interference pattern.
3. Intensity of Light:
- The intensity of the resultant light (IR) at any point on the screen is given by the formula:
IR=I1+I2+2√I1I2cos(ϕ)
- Here, I1 is the intensity from the upper slit (S1), I2 is the intensity from the lower slit (S2), and ϕ is the phase difference between the two waves.
4. Change in Intensities:
- If the slab absorbs some light, I1 will decrease, which will consequently affect the resultant intensity IR. Therefore, the intensity of the central maximum may change.
5. Central Maximum Shift:
- The introduction of a slab introduces an additional optical path difference. The path difference due to the slab is given by:
Δx=(n−1)T
- Here, n is the refractive index of the slab and T is the thickness of the slab. Since n>1, this path difference is positive, which means the central maximum will shift.
6. Intensity of Dark Fringe:
- The intensity of the dark fringe depends on the intensities I1 and I2. Since I1 may change due to the slab, the intensity of the dark fringe will not always be zero. It can vary based on the absorption characteristics of the slab.
Conclusion:
From the analysis, we conclude:
- Option A: The intensity of the central maximum may change - Correct.
- Option B: The intensity of the central maximum may not change if the slab does not absorb light - Correct.
- Option C: The central maximum will be shifted up due to the introduction of the slab - Correct.
- Option D: The intensity of the dark fringe will not always be zero - Incorrect.
Thus, the correct options are A, B, and C.
- In the YDSE, we have two slits (let's call them S1 and S2) and a light source placed symmetrically to these slits. A transparent slab is placed in front of the upper slit (S1).
- The transparent slab can absorb some light, which may change the intensity of the light coming from the upper slit (S1). This absorption can affect the overall intensity of the interference pattern.
- The intensity of the resultant light (IR) at any point on the screen is given by the formula:
IR=I1+I2+2√I1I2cos(ϕ)
- Here, I1 is the intensity from the upper slit (S1), I2 is the intensity from the lower slit (S2), and ϕ is the phase difference between the two waves.
- If the slab absorbs some light, I1 will decrease, which will consequently affect the resultant intensity IR. Therefore, the intensity of the central maximum may change.
- The introduction of a slab introduces an additional optical path difference. The path difference due to the slab is given by:
Δx=(n−1)T
- Here, n is the refractive index of the slab and T is the thickness of the slab. Since n>1, this path difference is positive, which means the central maximum will shift.
- The intensity of the dark fringe depends on the intensities I1 and I2. Since I1 may change due to the slab, the intensity of the dark fringe will not always be zero. It can vary based on the absorption characteristics of the slab.
From the analysis, we conclude:
- Option A: The intensity of the central maximum may change - Correct.
- Option B: The intensity of the central maximum may not change if the slab does not absorb light - Correct.
- Option C: The central maximum will be shifted up due to the introduction of the slab - Correct.
- Option D: The intensity of the dark fringe will not always be zero - Incorrect.
Topper's Solved these Questions
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Multiple Correct
8 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Assertion- Reasoning
13 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Subjective
11 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - single correct Ansewer type
12 Videos
Similar Questions
_E01_029_Q01.png)
In YDSE, the source placed symmetrically with respect to the slit is now moved parallel to the plane of the slits it is closer to the upper slit, as shown then
View SolutionIn YDSE, both slits produce equal intensities on the screen. A 100% transparent thin film is placed in front of one of the slits. Now, the intensity on the centre becomes 75% of the previous intensity. The wavelength of light is 6000Å and refractive index of glass is 1.5. Thus, minimum thickness of the glass slab is
View SolutionThe graph between the shifts of the interferring pattern in a double slit experiment with the thickness t of a transparent slab introduced in front of one of the slits is best represented by
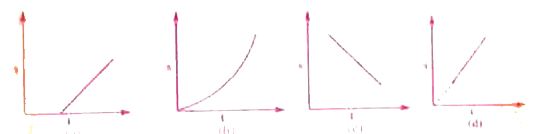
View SolutionIn YDSE, find the thickness of a glass slab (μ=1.5) which
should be placed in front of the upper slit S1 so that the central maximum now
lies at a point where 5th bright fringe was lying earlier (before inserting the
slab). Wavelength of light used is 5000Å.
View SolutionIn a Young's double slit experimental arrangement shown here, if a mica sheet of thickness t and refractive indec μ is placed in front of the slit S1, then the path difference (S1P−S2P) is

View SolutionThe slits in a Young's double slit experiment have equal width and the source is placed symmetrically with respect to the slits. The Intensity at the central fringe is I0. If one of the slits is closed, the intensity at this point will be
View SolutionA thin transparent sheet is placed in from of a Young's double slit. The fringe width will
View SolutionIn YDSE, water is filled in the space between the slits and screen. Then
View SolutionA point source of light is placed in front of a plane mirror.
View SolutionWhite light is used to illuminate the two slits in a Young's
double slit experiment. The separation between the slits is b and the screen is at
a distance d(>>b) from the slits. At a point on the screen directly in front of
one of the slits, certain wavelengths are missing. Some of these missing
wavelength are
View Solution