During the decay of current in an LR circuit, if the current falls to η times the intial value in time T, then determine the value of time constane.
To determine the value of the time constant τ during the decay of current in an LR circuit, we can follow these steps:
1. Understand the Current Decay Formula:
The current I in an LR circuit decays according to the formula:
I=I0e−tτ
where I0 is the initial current, t is the time, and τ is the time constant.
2. Set Up the Given Condition:
According to the problem, the current falls to η times its initial value after a time T. Therefore, we can express this as:
I=ηI0
and we know that this occurs at time T.
3. Substitute into the Decay Formula:
Substitute I=ηI0 into the decay formula:
ηI0=I0e−Tτ
4. Cancel I0:
Since I0 is common on both sides (assuming I0≠0), we can cancel it:
η=e−Tτ
5. Take the Natural Logarithm:
To solve for τ, take the natural logarithm of both sides:
ln(η)=−Tτ
6. Rearrange to Solve for τ:
Rearranging the equation gives:
τ=−Tln(η)
7. Express in Terms of ln(1/η):
Since ln(η) can be expressed as −ln(1/η), we can rewrite τ as:
τ=Tln(1/η)
Final Answer:
The time constant τ is given by:
τ=Tln(1/η)
---
The current I in an LR circuit decays according to the formula:
I=I0e−tτ
where I0 is the initial current, t is the time, and τ is the time constant.
According to the problem, the current falls to η times its initial value after a time T. Therefore, we can express this as:
I=ηI0
and we know that this occurs at time T.
Substitute I=ηI0 into the decay formula:
ηI0=I0e−Tτ
Since I0 is common on both sides (assuming I0≠0), we can cancel it:
η=e−Tτ
To solve for τ, take the natural logarithm of both sides:
ln(η)=−Tτ
Rearranging the equation gives:
τ=−Tln(η)
Since ln(η) can be expressed as −ln(1/η), we can rewrite τ as:
τ=Tln(1/η)
The time constant τ is given by:
τ=Tln(1/η)
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Solved Examples3videos
INDUCTANCE
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Exercise 4.124videos
INDUCTANCE
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Thermal Power in Resistance Connected in Circuit27videos
HEATING EFFECT OF CURRENT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Multiple Correct Answer type2videos
MAGNETIC FIELD AND MAGNETIC FORCES
Similar Questions
The value of current I in the circuit will be
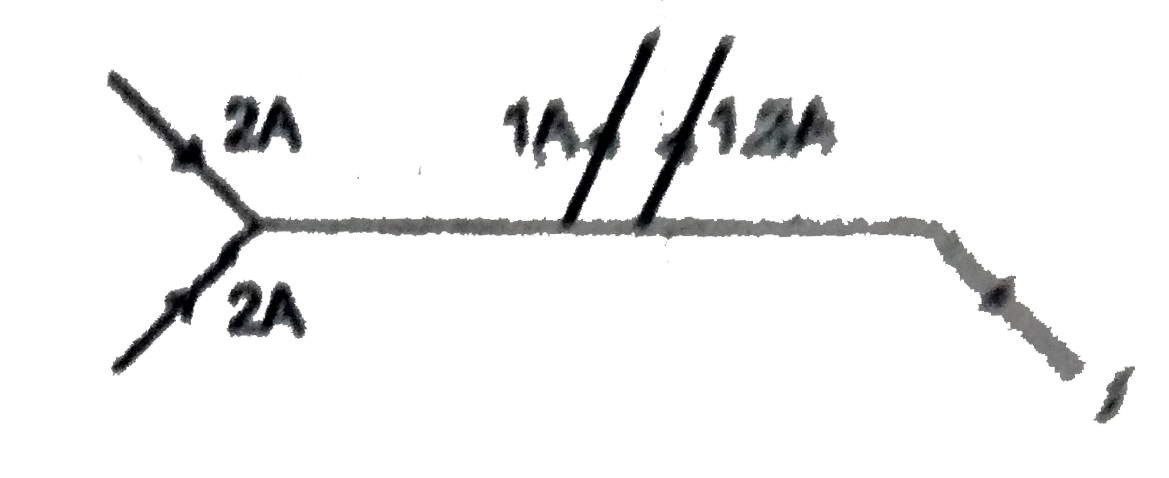 View Solution
View SolutionWhen a choke coil carrying a steady current is short circuited, the current in it decreases to β(<1) times its initial value in a time T. The time constant of the choke coil is
View SolutionTime constant of LR circuit will be
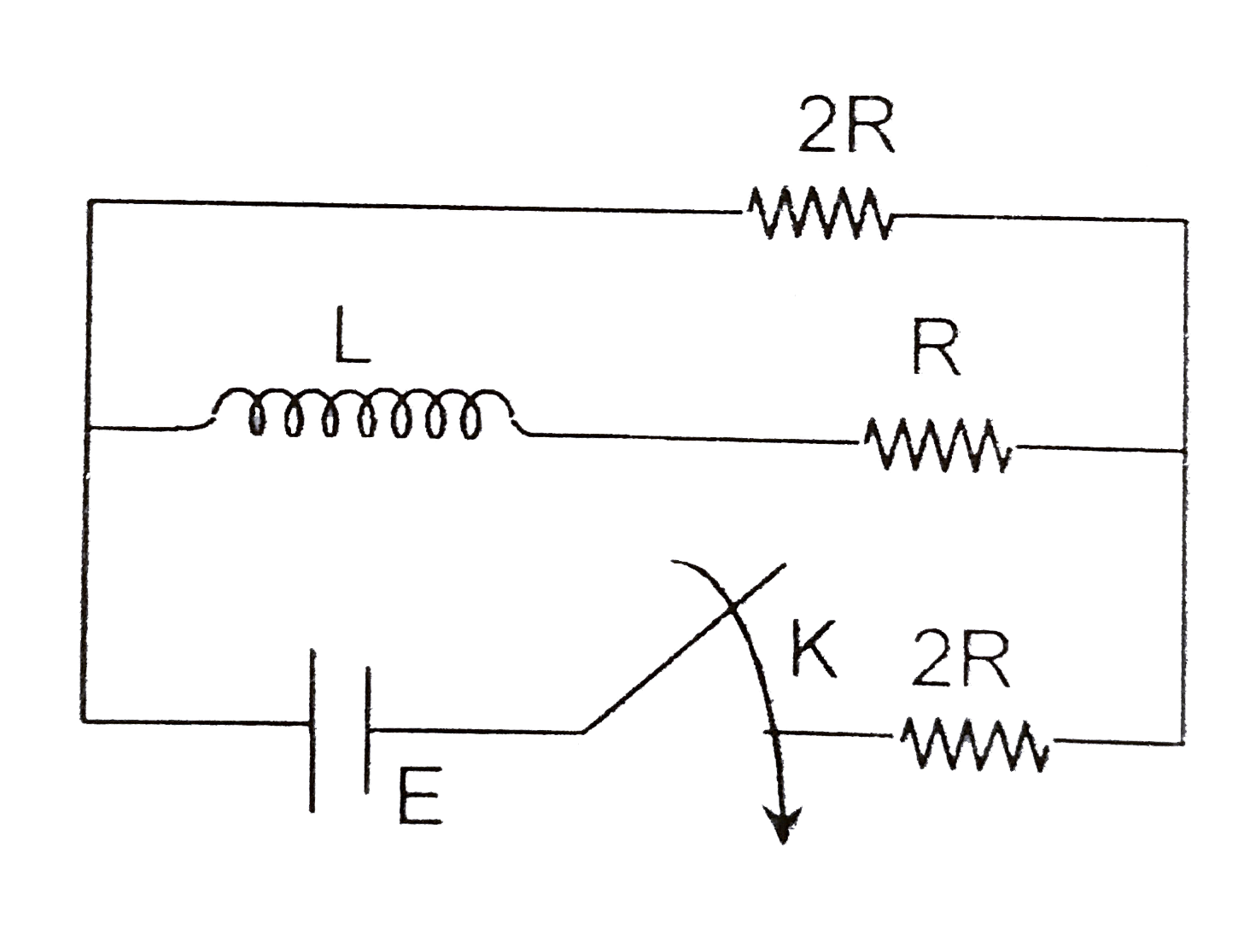 View Solution
View SolutionIn the given circuit , the value of current is
 View Solution
View Solution
In given LR circuit the switch S is closed at time t=0 thenView SolutionThe current in an L−R circuit builds upto 3/4th of its steady state value in 4sec. Then the time constant of this circuit is
View SolutionDuring current growth in an L-R circuit the time constant is the time in which the magnitude of current becomes
View SolutionDuring discharging of a capacitor via a resistor

Circuit current varies with time asView SolutionDuring charging of capacitor in the circuit shown,

Circuit current versus time graph isView SolutionIn the given circuit, what is the current I (in A) drawn from battery at time t = 0.
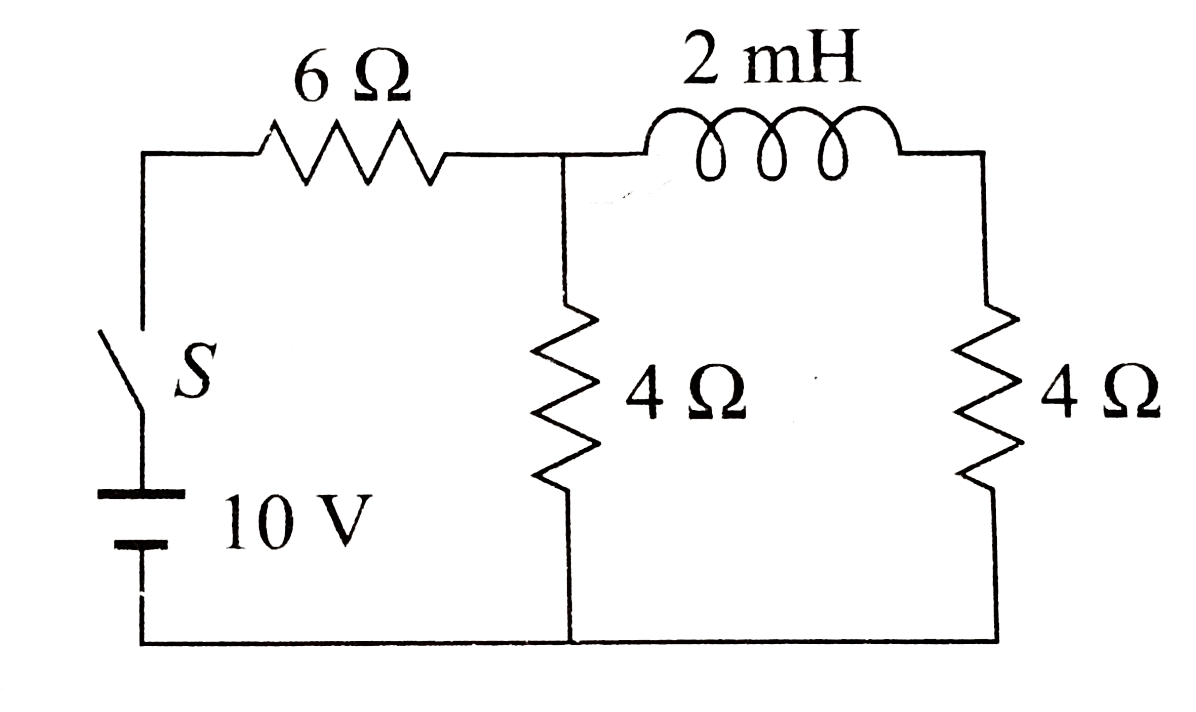 View Solution
View Solution

