A small square loop of edge a and resistance R is moved with velocity v0 away from an infinitely long current carrying conductor carrying current I so that the conductor and side of square are always in same plane. Find induced current in loop at a separation of r
μ0ia2vπr2R
μ0ia2v4πr2R
μ0ia2v2πr2R
μ0iav2πrR
The correct Answer is:C
To find the induced current in a small square loop of edge a and resistance R that is moved with velocity v0 away from an infinitely long current-carrying conductor carrying current I, we can follow these steps:
Step 1: Determine the Magnetic Field
The magnetic field B at a distance r from an infinitely long straight conductor carrying current I is given by the formula:
B=μ0I2πr
where μ0 is the permeability of free space.
Step 2: Express the Distance
As the loop moves away from the conductor with velocity v0, the distance r from the conductor at time t can be expressed as:
r=r0+v0t
where r0 is the initial distance from the conductor.
Step 3: Calculate the Magnetic Field as a Function of Time
Substituting r into the magnetic field equation, we get:
B(t)=μ0I2π(r0+v0t)
Step 4: Calculate the Magnetic Flux
The magnetic flux Φ through the square loop of area A=a2 is given by:
Φ=B(t)⋅A=μ0I2π(r0+v0t)⋅a2
Step 5: Differentiate the Magnetic Flux to Find EMF
The induced EMF E is given by Faraday's law of electromagnetic induction:
E=−dΦdt
Differentiating the flux with respect to time:
E=−ddt(μ0Ia22π(r0+v0t))
Using the chain rule, we find:
E=μ0Ia2v02π(r0+v0t)2
Step 6: Calculate the Induced Current
Using Ohm's law, the induced current I′ can be calculated as:
I′=ER=μ0Ia2v02πR(r0+v0t)2
Final Result
Thus, the induced current in the loop at a separation of r is:
I′=μ0Ia2v02πR(r0+v0t)2
---
The magnetic field B at a distance r from an infinitely long straight conductor carrying current I is given by the formula:
B=μ0I2πr
where μ0 is the permeability of free space.
As the loop moves away from the conductor with velocity v0, the distance r from the conductor at time t can be expressed as:
r=r0+v0t
where r0 is the initial distance from the conductor.
Substituting r into the magnetic field equation, we get:
B(t)=μ0I2π(r0+v0t)
The magnetic flux Φ through the square loop of area A=a2 is given by:
Φ=B(t)⋅A=μ0I2π(r0+v0t)⋅a2
The induced EMF E is given by Faraday's law of electromagnetic induction:
E=−dΦdt
Differentiating the flux with respect to time:
E=−ddt(μ0Ia22π(r0+v0t))
Using the chain rule, we find:
E=μ0Ia2v02π(r0+v0t)2
Using Ohm's law, the induced current I′ can be calculated as:
I′=ER=μ0Ia2v02πR(r0+v0t)2
Thus, the induced current in the loop at a separation of r is:
I′=μ0Ia2v02πR(r0+v0t)2
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Multiple Correct34videos
MISCELLANEOUS VOLUME 5
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Linked Comprehension84videos
MISCELLANEOUS VOLUME 5
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - True and False3videos
MISCELLANEOUS VOLUME 3
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NUCLEAR PHYSICSEXERCISE - ddp.5.514videos
NUCLEAR PHYSICS
Similar Questions
The strength of magnetic field around an infinitely long current carrying conductor is
View SolutionA rod having length l and resistance R is moving with velocity v on a π shape conductor. Find the current in the rod.
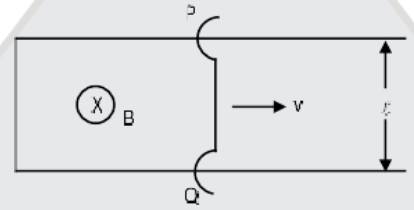 View Solution
View Solutiona rectangular loop, as shown in Fig. 3.66, moves away from an infinitely long wire carrying a current I. Find the emf induced in the rectangualr loop.
 View Solution
View Solutiona rectangular loop, as shown in Fig. 3.66, moves away from an infinitely long wire carrying a current I. Find the emf induced in the rectangualr loop.
 View Solution
View SolutionA long current carrying wire, carrying current such that it is flowing out from the plane of paper, is placed at O. A steady state current is flowing in the loop ABCD. Then,
 View Solution
View SolutionA conducting circular loop of radius a and resistance per unit length R is moving with a constant velocity v0 , parallel to an infinite conducting wire carrying current i0. A conducting rod of length 2a is approaching the centre of the loop with a constant velocity v02 along the direction 2 of the current. At the instant t=0, the rod comes in contact with the loop at A and starts sliding on the loop with the constant velocity. Neglecting the resistance of the rod and the self-inductance of the circuit, find the following when the rod slides on the loop.
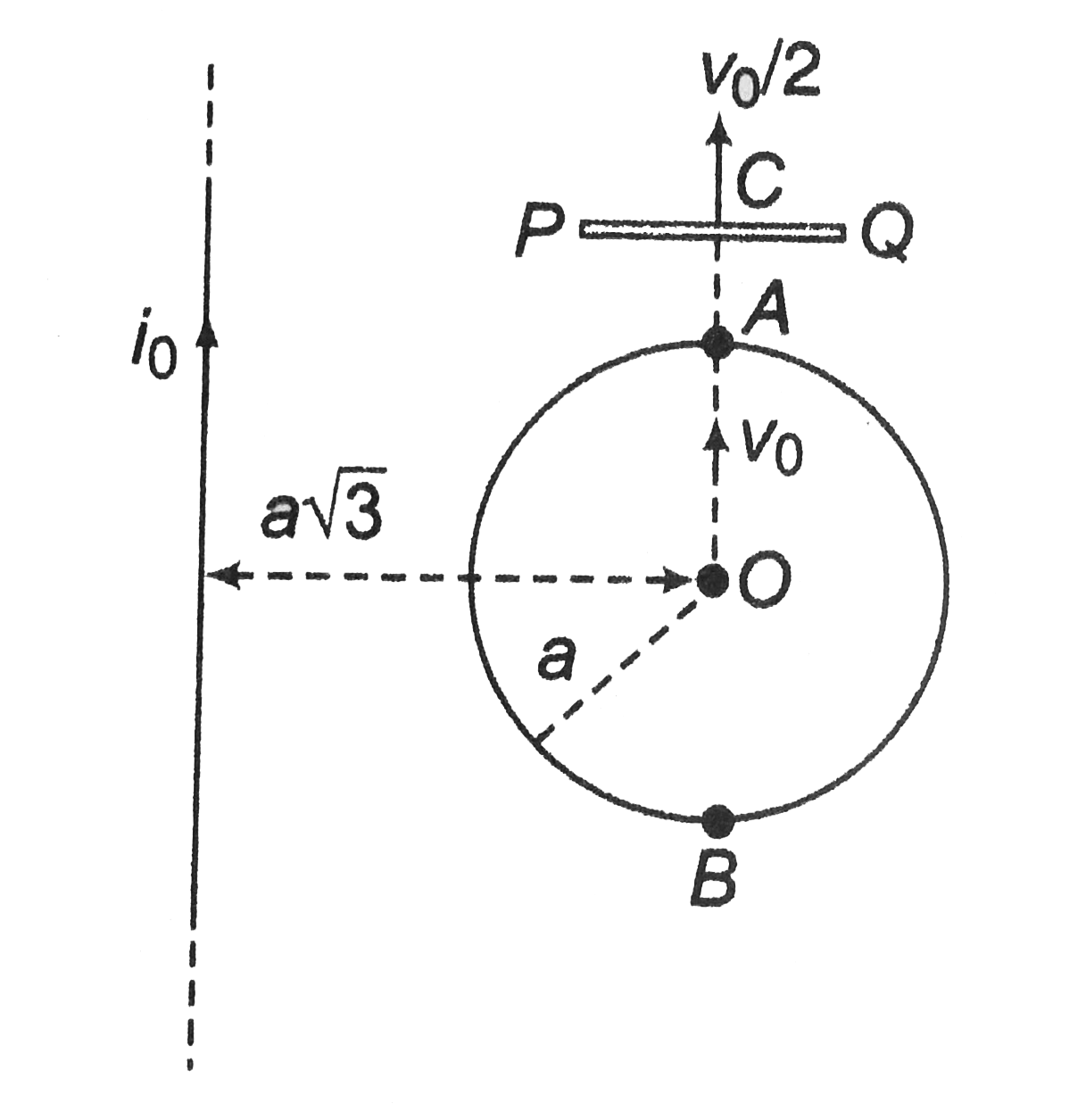
(a) The current through the rod when it is at a distance of (a2) from the point A of the loop.
(b) Force required to maintain the velocity of the rod at that instant.View SolutionA square loop, carrying a steady current I, is placed in a horizontal plane near a long staright conductor carryinf a steady current I, at a distance d from the conductor as shown in Fig. The loop wil experience
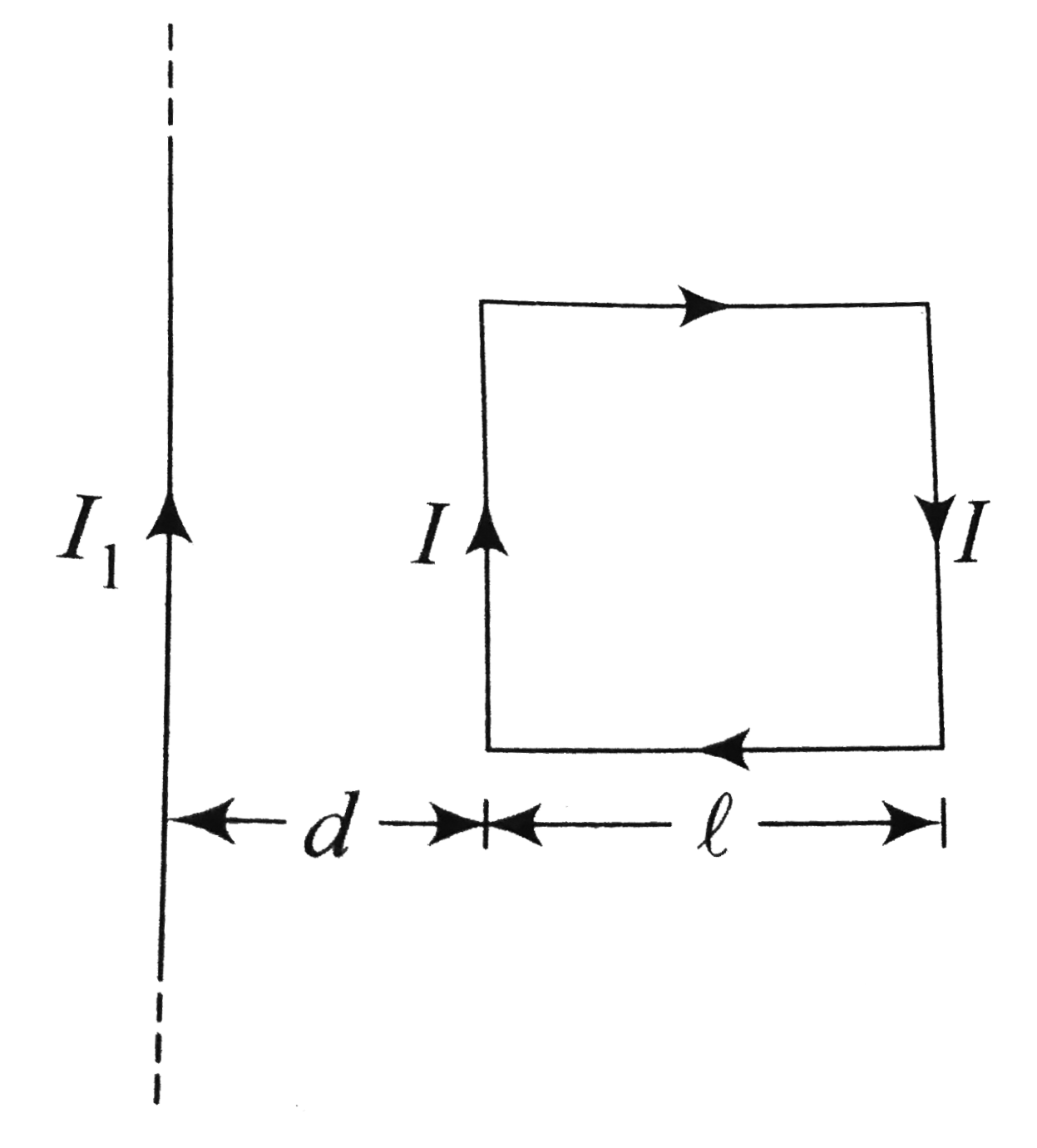 View Solution
View SolutionA square loop, carrying a steady current I, is placed in a horizontal plane near a long straight conductor carrying a steady current I1 at a distance d from the donductor as shown in figure. The loop will experience
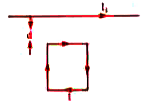 View Solution
View SolutionAn infinite current-carrying conductor is placed along the z-axis and a wire loop is kept in the x−y plane. The current in the conductor is increasing with time. Then the
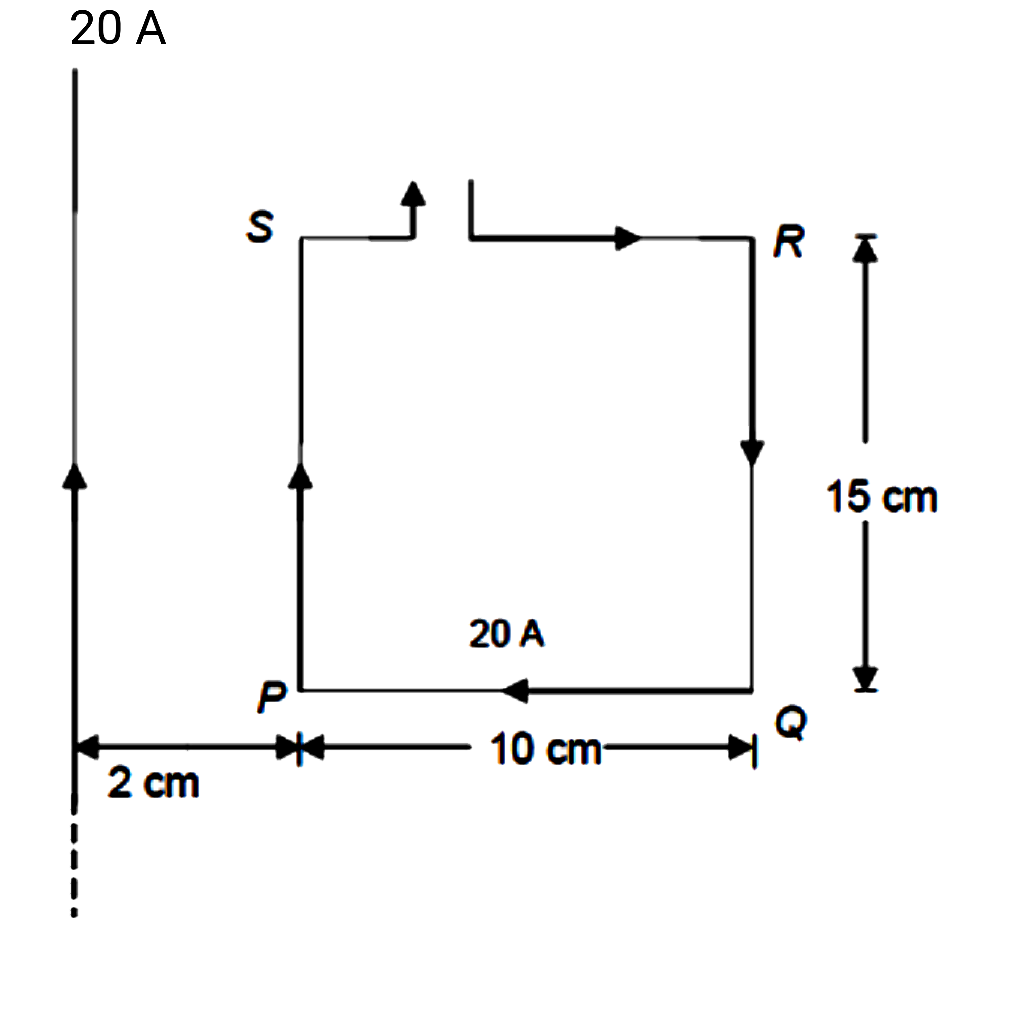
View SolutionThe resultant force (inμN) on the current loop PQRS due to a long current - carrying conductor (current = 20 A) will be
 View Solution
View Solution

