An infinite cylindrical wire of radius R and having current density varying with its radius r as, J=J0[1−(r/R)]. Then answer the following questions.
![An infinite cylindrical wire of radius R and having current density varying with its radius r as, J = J(0)[1-(r//R)]. Then answer the following questions. Graph between the magnetic field and radius is](https://d10lpgp6xz60nq.cloudfront.net/physics_images/BMS_V05_MCA_E01_140_Q01.png)
Graph between the magnetic field and radius is
J0R6μ0
316J0Rμ0
516J0Rμ0
56J0Rμ0
The correct Answer is:B
Current with in radius r:I=∫rJdA
⇒I=∫r0J0[1−RR]2πrdr=2πj0[r22−r33R]
Apply ampere's law B2πr=μ0I
B2πr=μ02πJ0(r22−r33R)⇒B=μ0J0[r2−r23R]
to find max B: dBdr=0⇒r=3R/4
Bmax=μ0J90[3R/42−(3R/4)23r]=3R16μ0J0.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Integer12videos
MISCELLANEOUS VOLUME 5
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Multiple Correct34videos
MISCELLANEOUS VOLUME 5
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - True and False3videos
MISCELLANEOUS VOLUME 3
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NUCLEAR PHYSICSEXERCISE - ddp.5.514videos
NUCLEAR PHYSICS
Similar Questions
A cylindrical wire of radius R has current density varying with distance r form its axis as J(x)=J0(1−r2R2) . The total current through the wire is
View SolutionAn infinitely long cylinderical wire of radius R is carrying a current with current density j=αr3 (where α is constant and r is the distance from the axis of the wire). If the magnetic fixed at r=R2 is B1 and at r=2R is B2 then the ratio B2B1 is
View SolutionMagnetic field in cylindrical region of radius R in inward direction is as shown in figure.
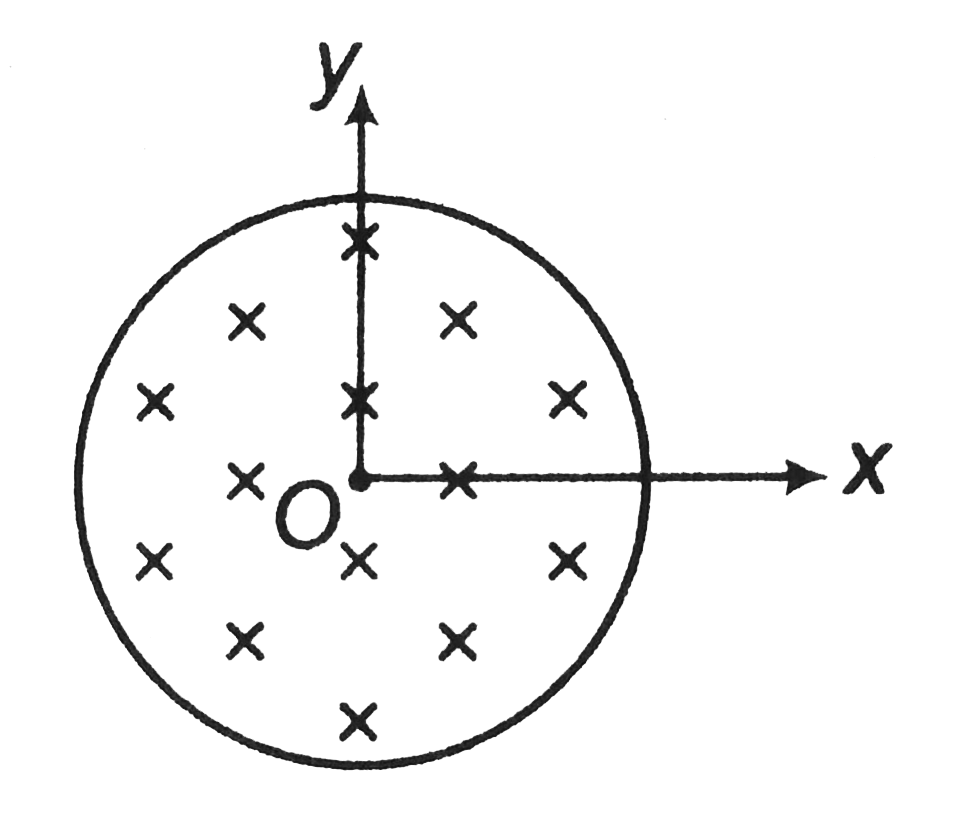 View Solution
View SolutionA current is flowing through a cylinderical conductor of radius R, such that current density at any cross-section is given by J=J0(1−rR), where r is radial distance from axis of the cylinder .Calculate the total current through the cross-section of the conductor.
View SolutionA cylindrical long wire of radius R carries a current I uniformly distributed over the cross sectional area of the wire. The magnetic field at a distance x from the surface inside the wire is
View SolutionA long straight conducting solid cylindrical wire of radius R carries a steady current / that is uniformly distributed throughout the cross section of the wire. Draw graph of magnetic field B versus r (where r is distance from the axis of the wire)
View SolutionAn Infinite current carrying wire having current I0 is placed coaxially inside a hollow conducting infinite cylinder of radius R and having current I flowing along the length of the cylinder in the same direction as I0 what is the increment in magnetic pressure due to placing of the wire?
View SolutionA current I is flowing in a straight conductor of length L. The magnetic induction at a point distant L4 from its centre will be
View SolutionA long cylindrical conductor of radius R carries a current i as shown in the figure. The current density J varies across the cross-section as J=kr2, where, k is a constant. Find an expression for the magnetic field B at a distance r(<R) from the axis
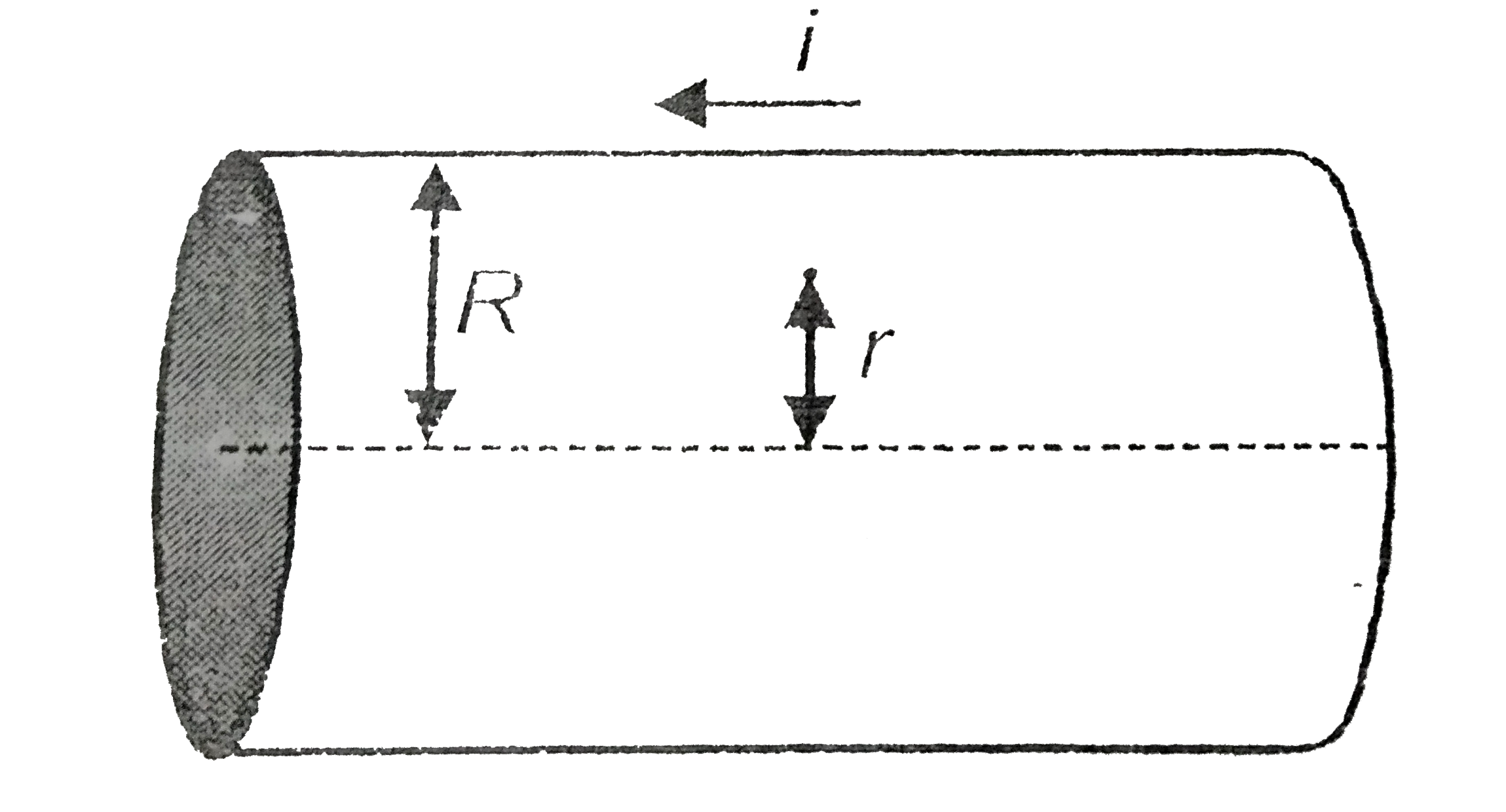 View Solution
View SolutionThe current density across a cylindrical conductor of radius R varies in magnitude according to the equation J=J0(1−rR) where r is the distance from the central axis. Thus, the current density is a maximum J0 at that axis (r = 0) and decreases linearly to zero at the surface (r = R). Calculate the current in terms of J0 and the conductor 's cross - sectional area A=πR2.
View Solution

