figure show the identical simple pan-delums of length. One is tilled at an angle α and imparted an initial velocity v1 towards mean possition and at a velocity v2 at an initial angular displacement β. Find the phase difference in oscillations of these two pendulums

It is given that first pendulum bob is given a velocity v1 at a dislpacement lα from mean position , using the formula for velocity we can find the amplitude of its oscillation as
V1=ω√A21−(lα)2 [If A1, is the amplitude of SHM of this As for simple pendulum ω=√gl we have
V21=gl[(A21)−(lα)2)]
A1=√l2α2+v21lg (i)
Similarly if A2 is the amplitude of SHM of second pendlum bob we have
V2=ω√A21−(lβ)2
or A2=
⎷(l2β2+v22lg) (ii)
Now we repersent the two SHMs by circular motion representation as shown in figure
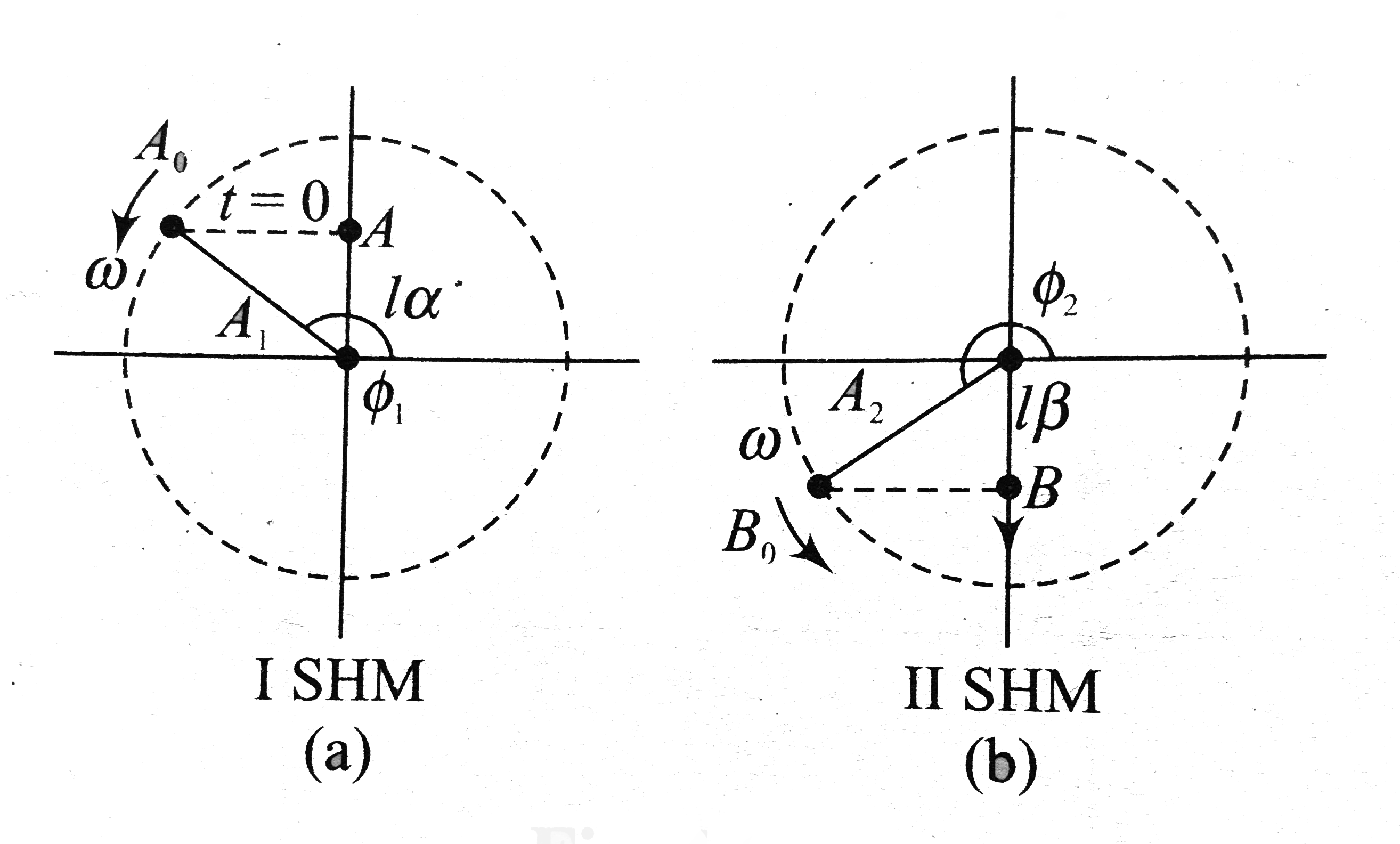
In first pendulum at t=0 the bob is thrown from a displacement lα from mean position with a velocity v1 towards mean position . As it is moving towards mean position in figure (a) , we consider the corresponding circular motion particle A0 of the bob A is second quarant, as the referance direction of ω we consider anticlockwise. As shown in figure initial phase of bob A is given as
ϕ1=π−sin−1(lαA1) (iii)
Similarly for second pendulum bob B, its corresponding circular motion partical B0att=0 is consider as shown in figure (b) its initial base is given as
ϕ2=sin−1(lβA2) (iv)
As both the pandulum are identical, their angular frequency for SHM must be same , so their phase difference can be given as
Δϕ=ϕ2−ϕ1sin−1(lβA2)+sin−1(lαA1)−π
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Solved Example15videos
LINEAR AND ANGULAR SIMPLE HARMONIC MOTION
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Exercise 4.123videos
LINEAR AND ANGULAR SIMPLE HARMONIC MOTION
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger11videos
KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type3videos
MISCELLANEOUS KINEMATICS
Similar Questions
If the second pendulum bob is thrown at velocity v2 at an angle β from mean position, but on other side of mean position , find the phase diffrence in the two SHMs now as show in the figure.
 View Solution
View SolutionLet there are three equal masses situated at the vertices of an equilateral triangle, as shown in Fig. Now particle A starts with a velocity v1 towards line AB, particle B starts with the velocity v2, towards line BC and particle C starts with velocity v3 towards line CA. Find the displacement of the centre of mass of the three particles A,B and C after time t. What would it be if v1=v2=v3?
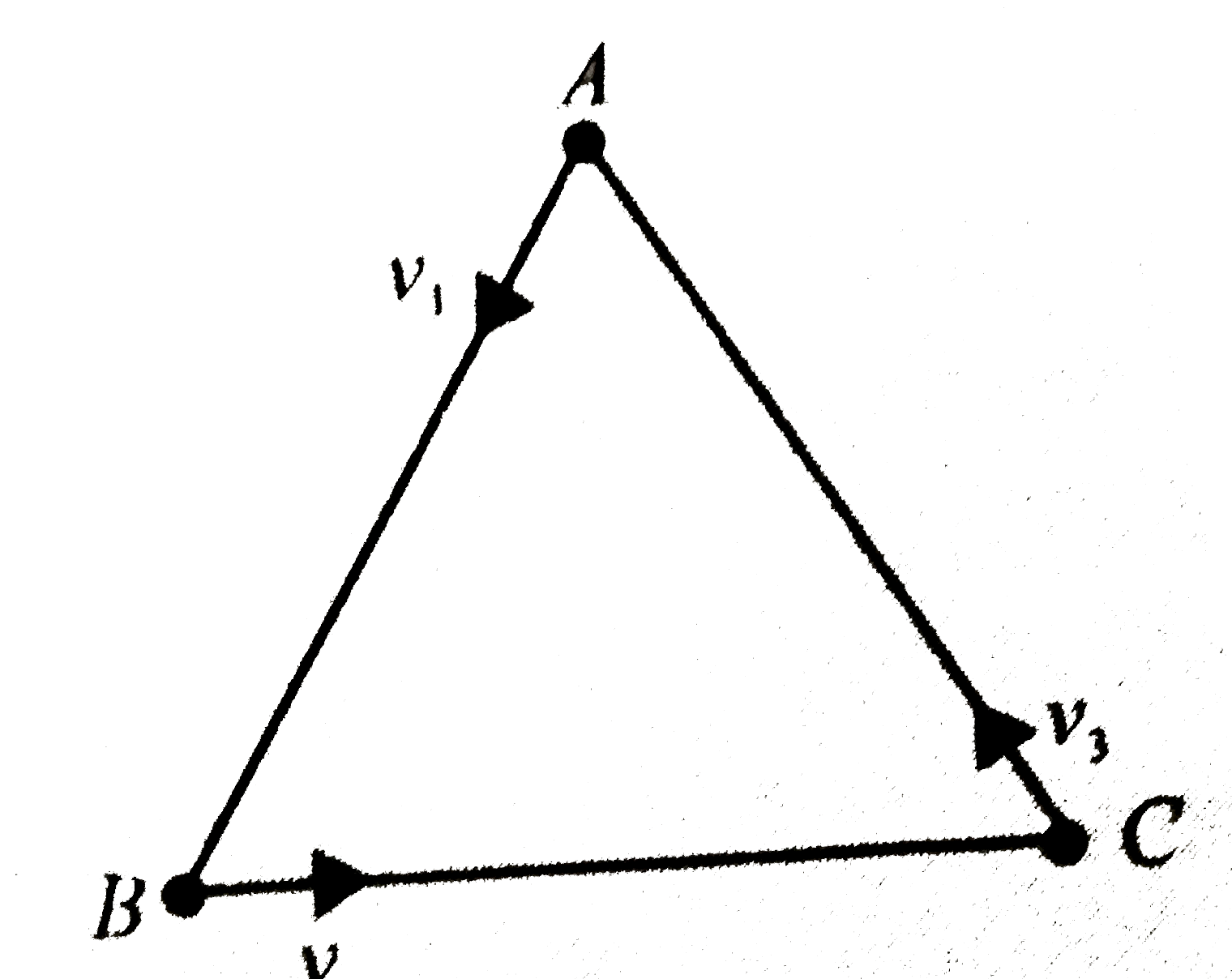 View Solution
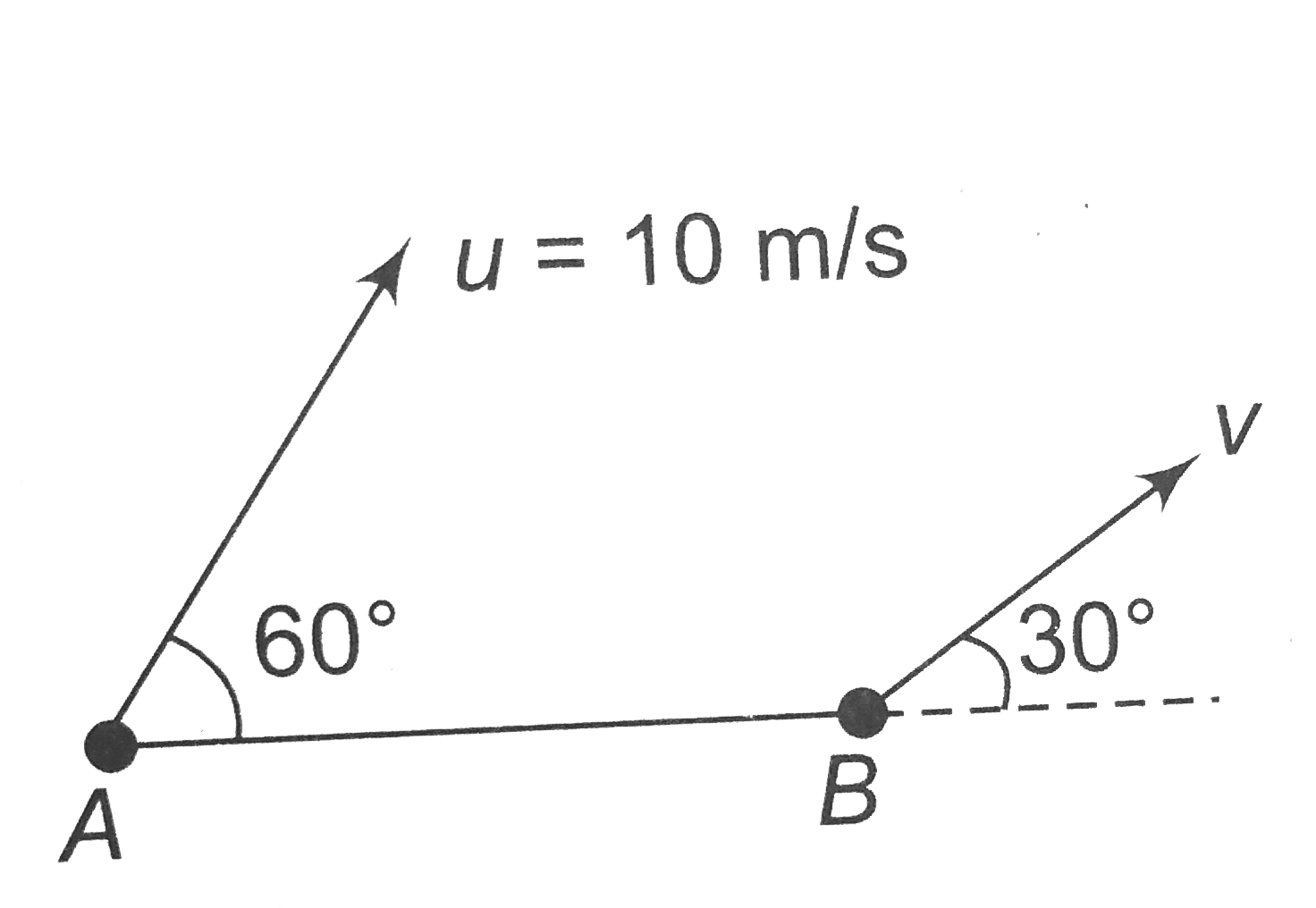
View SolutionTwo particles A and B are situated at a distance d=2m apart. Particle A has a velocity of 10m/s at an angle of 60∘ and particle B has a velocity v at an angle 30∘ as shown in figure. The distance d between A and B is constant. the angular velocity of B with respect to A is :
 .View Solution
.View SolutionTwo identical pendulums oscillate with a constant phase difference π4 and same amplitude. If the maximum velocity of one is v, the maximum velocity of the other will be.
View SolutionThe rod of length l=1m rotates with an angular velocity ω=2rads−1 an the point P moves with velocity v=1ms−1 and acceleration a=1ms−2. Find the velocity and acceleration of Q.
 View Solution
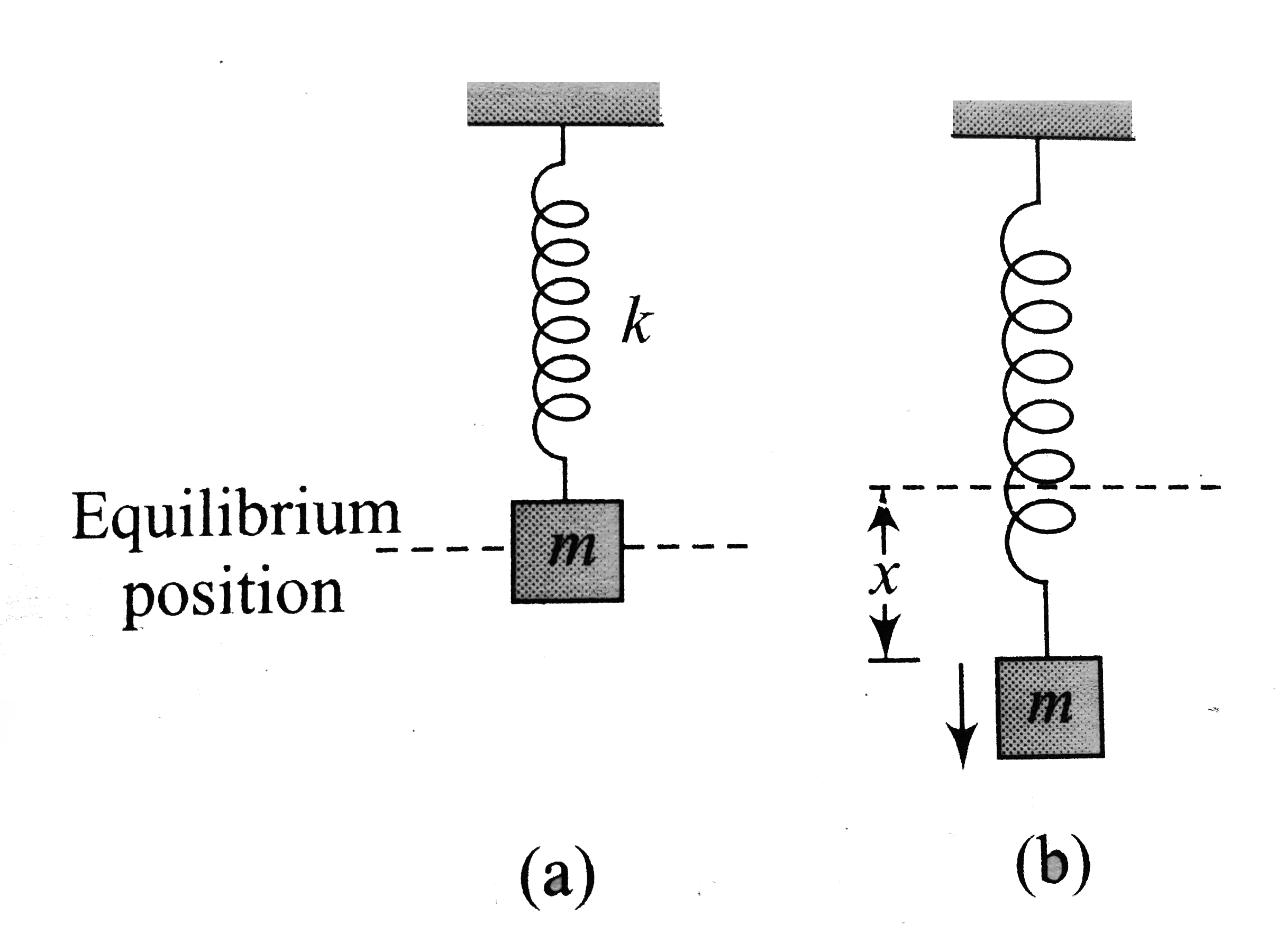
View SolutionFigure shown a spring block system hanging in equilibrium. The block of system is pulled down by the distance x and imparted a velocity v in downward direction as shown in figure. Find the time it will take to reach its mean position. Also find the maximum distance to which if will move before returning back towards mean position.
 View Solution
View SolutionPower of the only force acting on a particle of mass m=1 kg moving in straight line depends on its velocity as P=v2 where v is in m/s and P is in watt. If initial velocity of the particle is 1m/s, then the displacement of the particle in ln2 second will be :
View SolutionA proton is moving along the negative direction of X-axis in a magnetic field directed along the positive direction of Y-axis. The proton will be deflected along the negative direction of
View SolutionTwo identical simple pendulums A and B are fixed at same point. They are displaced by very small angles α and β(β>α) and released from rest. Find the time after which B reaches its initial position for the first time. Collisions are elastic and length of strings is l.
 View Solution
View SolutionAssertion : The average velocity of a particle having initial and final velocity v1 and v2 is v1+v2/2.
Reason : If r1 and r2 be the initial and final displacement in time t, then vav=r1−r2t .View Solution

