If the second pendulum bob is thrown at velocity v2 at an angle β from mean position, but on other side of mean position , find the phase diffrence in the two SHMs now as show in the figure.

In this case , amplitudes of the two SHMs will still remain the same and are given by Eqs (i) and (ii) but when we represent the two SHM s on their corresponding circular motion , the position of the partical of the principal in circular motion , the position of the partical in circular motion in second pendulum is now difference as shown in figure .
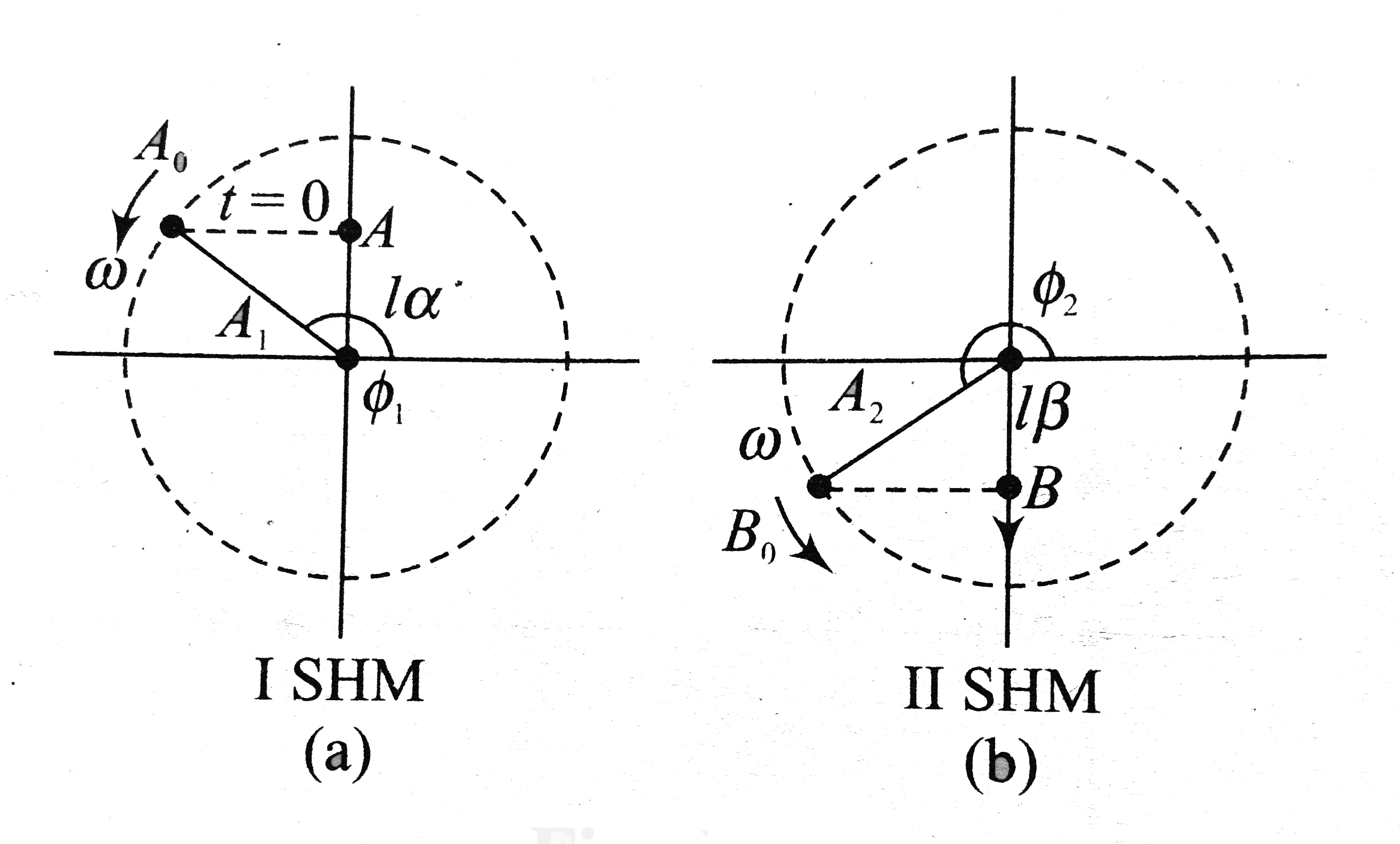
As shown in figure (a) and (b) the initial phase of the two pendulum bobs are
ϕ1=π−sin−1(lαA1)andϕ2=π+sin−1(lβA2)
As ω for both SHm are same, their phase difference remain constant so it is given as
Δϕ2−π1=sin−1(lβA2)+sin−1(lαA1)
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Solved Example15videos
LINEAR AND ANGULAR SIMPLE HARMONIC MOTION
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Exercise 4.123videos
LINEAR AND ANGULAR SIMPLE HARMONIC MOTION
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger11videos
KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type3videos
MISCELLANEOUS KINEMATICS
Similar Questions
Two simple pendulums of equal length cross each other at mean position. What is their phase difference ?
View Solutiontwo partical excuting SHM with same frequency and amplitudes Aand2A on same straight line with same mean position cross each other in opposite direction at a distance A/3 from mean possion. Find the phase difference in the two SHM s.
View SolutionA pendulum is displaced to an angle θ from its equilibrium position, then it will pass through its mean position with a velocity v equal to
View SolutionTwo simple pendulums have time period 4s and 5s respectively. If they started simultaneously from the mean position in the same direction, then the phase difference between them by the time the larger one completes one oscillation is
View SolutionIf a graph is plotted between velocity (v) and displacement (y) of a particle executing SHM from mean position, then the nature of the graph is
View SolutionIt takes 0.2 s for a pendulum bob to move from the mean position to one end. What is the time period of the pendulum?
View SolutionThe figure shows a graph between velocity and displacement (from mean position) of a particle performing SHM:
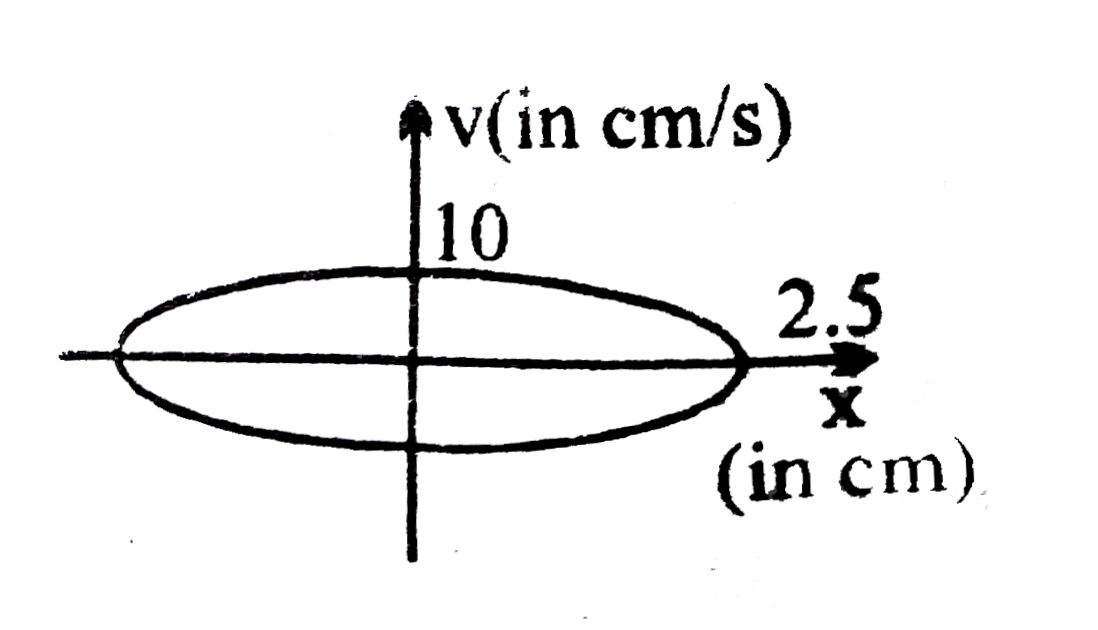 View Solution
View Solutionfigure show the identical simple pan-delums of length. One is tilled at an angle α and imparted an initial velocity v1 towards mean possition and at a velocity v2 at an initial angular displacement β. Find the phase difference in oscillations of these two pendulums
 View Solution
View SolutionA particle executing SHM has velocities u and v and acceleration a and b in two of its position. Find the distance between these two positions.
View SolutionThe figure below shows a simple pendulum of mass 200 g. It is displaced from the mean position A to the extreme position B. The potential energy at the position A is zero. At the position B the pendulum bob is raised by 5 m.
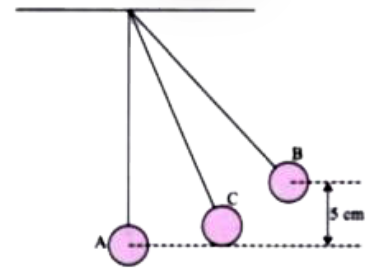
(i) What is the potential energy of the pendulum at the position B?
(ii) What is the total mechanical energy at point C?
(iii) What is the speed of the bob at the position A when released from B ?
(Take g = 10ms−2 and there is no loss of energy.)View Solution

