An interference is observed due to two coherent sources S1 placed at origin and S2 placed at (0,3λ,0). Here, lambda is the wavelength of the sources. A detector D is moved along the positive x-axis. Find x-coordinates on the x-axis (excluding x=0andx=∞) where maximum intensity is observed.
To find the x-coordinates on the x-axis where maximum intensity is observed due to the interference of light from two coherent sources S1 and S2, we can follow these steps:
Step 1: Understand the setup
The sources are located at:
- S1 at the origin (0,0)
- S2 at (0,3λ,0)
The detector D is moved along the positive x-axis.
Step 2: Path difference condition for maxima
For constructive interference (maximum intensity), the path difference S2P−S1P must be an integer multiple of the wavelength λ:
S2P−S1P=nλ(n=0,1,2,…)
Step 3: Calculate the distances
Let P be a point on the x-axis at (x,0).
- The distance from S1 to P is:
S1P=√x2+02=x
- The distance from S2 to P is:
S2P=√x2+(3λ)2=√x2+9λ2
Step 4: Set up the equation for maxima
For the first order maximum (n=1):
√x2+9λ2−x=λ
Step 5: Solve for x
Squaring both sides:
x2+9λ2−2x√x2+9λ2+x2=λ2
This simplifies to:
2x2+9λ2−λ2=2x√x2+9λ2
2x2+8λ2=2x√x2+9λ2
Dividing by 2:
x2+4λ2=x√x2+9λ2
Squaring again:
(x2+4λ2)2=x2(x2+9λ2)
Expanding both sides:
x4+8x2λ2+16λ4=x4+9x2λ2
This leads to:
8x2λ2+16λ4=9x2λ2
Rearranging gives:
−x2λ2+16λ4=0
Factoring out λ2:
−x2+16λ2=0
Thus:
x2=16λ2⟹x=4λ
Step 6: Find the second order maximum
For the second order maximum (n=2):
√x2+9λ2−x=2λ
Following similar steps as above, we find:
x2+4λ2=x√x2+9λ2
Squaring and simplifying, we will eventually find:
x=1.25λ
Final Result
The x-coordinates where maximum intensity is observed are:
- x=1.25λ
- x=4λ
The sources are located at:
- S1 at the origin (0,0)
- S2 at (0,3λ,0)
For constructive interference (maximum intensity), the path difference S2P−S1P must be an integer multiple of the wavelength λ:
S2P−S1P=nλ(n=0,1,2,…)
Let P be a point on the x-axis at (x,0).
- The distance from S1 to P is:
S1P=√x2+02=x
- The distance from S2 to P is:
S2P=√x2+(3λ)2=√x2+9λ2
For the first order maximum (n=1):
√x2+9λ2−x=λ
Squaring both sides:
x2+9λ2−2x√x2+9λ2+x2=λ2
This simplifies to:
2x2+9λ2−λ2=2x√x2+9λ2
2x2+8λ2=2x√x2+9λ2
Dividing by 2:
x2+4λ2=x√x2+9λ2
Squaring again:
(x2+4λ2)2=x2(x2+9λ2)
Expanding both sides:
x4+8x2λ2+16λ4=x4+9x2λ2
This leads to:
8x2λ2+16λ4=9x2λ2
Rearranging gives:
−x2λ2+16λ4=0
Factoring out λ2:
−x2+16λ2=0
Thus:
x2=16λ2⟹x=4λ
For the second order maximum (n=2):
√x2+9λ2−x=2λ
Following similar steps as above, we find:
x2+4λ2=x√x2+9λ2
Squaring and simplifying, we will eventually find:
x=1.25λ
The x-coordinates where maximum intensity is observed are:
- x=1.25λ
- x=4λ
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHTEXERCISE - Exercise 32.13videos
INTERFERENCE AND DIFFRACTION OF LIGHT
- BOOK - DC PANDEY ENGLISHCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHTEXERCISE - Exercise 32.26videos
INTERFERENCE AND DIFFRACTION OF LIGHT
- BOOK - DC PANDEY ENGLISHCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHTEXERCISE - Example Type 63videos
INTERFERENCE AND DIFFRACTION OF LIGHT
- BOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - All Questions135videos
GRAVITATION
- BOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Medical entrance s gallery59videos
MAGNETIC FIELD AND FORCES
Similar Questions
An interference is observed due to two coherent sources S1 placed at origin and S2 placed at (0,3λ,0). Here, lambda is the wavelength of the sources. A detector D is moved along the positive x-axis. Find x-coordinates on the x-axis (excluding x=0andx=∞) where maximum intensity is observed.
View SolutionTwo coherent sources S1 and S2 area separated by a distance four times the wavelength λ of the source. The sources lie along y axis whereas a detector moves along +x axis. Leaving the origin and far off points the number of points where maxima are observed is
View SolutionTwo coherent light sources A and B are at a distance 3λ from each other (λ=wavelength)The distances from A on the X-axis at which the interference is constructive are
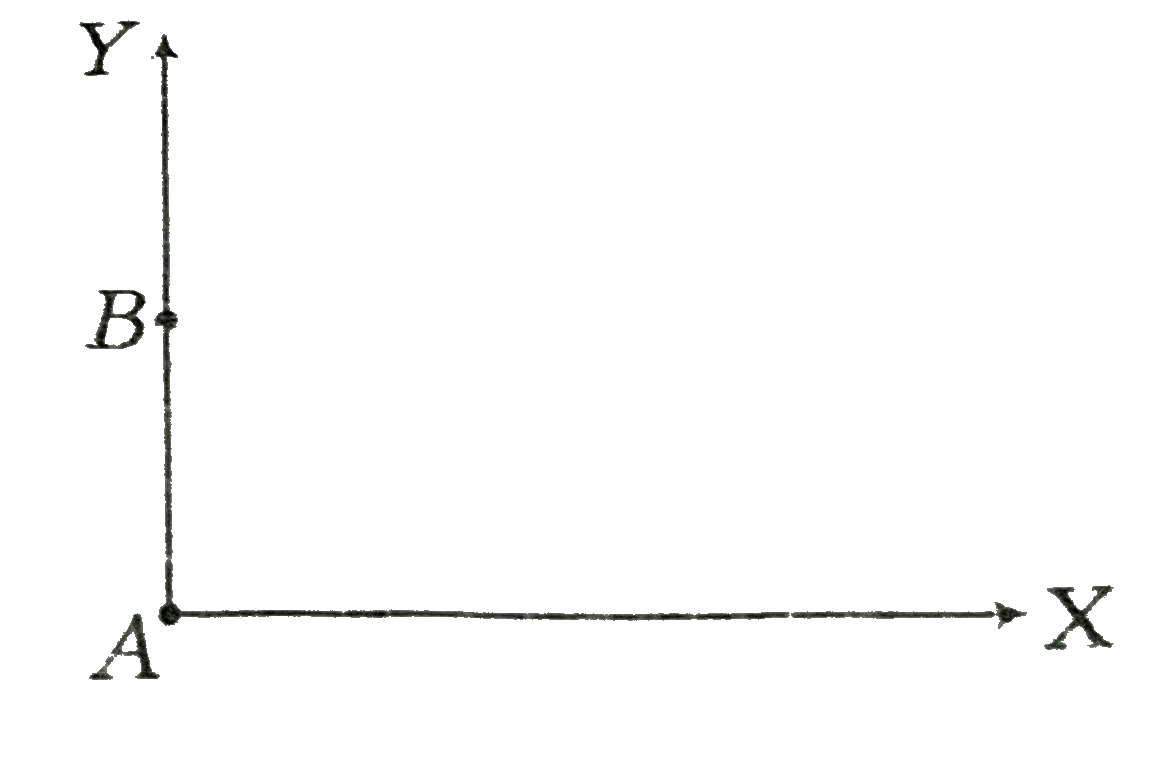 View Solution
View SolutionTwo coherent sources Sf and S2 (in phase with ech other) are placed at a distance of 2λ as shown where λ is wavelength of sound. A detector moves on line AB parrallel to S1S2. If detector detects maximum intensity at finite distance from O at θ=±(πn). Find n
 View Solution
View SolutionTwo identical coherent sources of wavelength λ are placed at (100λ,0) and (−50λ,0) along x-axis. The number of maxima and minima detected are ,respectively [include origin and (5λ,0)]
View SolutionTwo coherent sources emit light of wavelength λ. Separation between them, d=4λ.
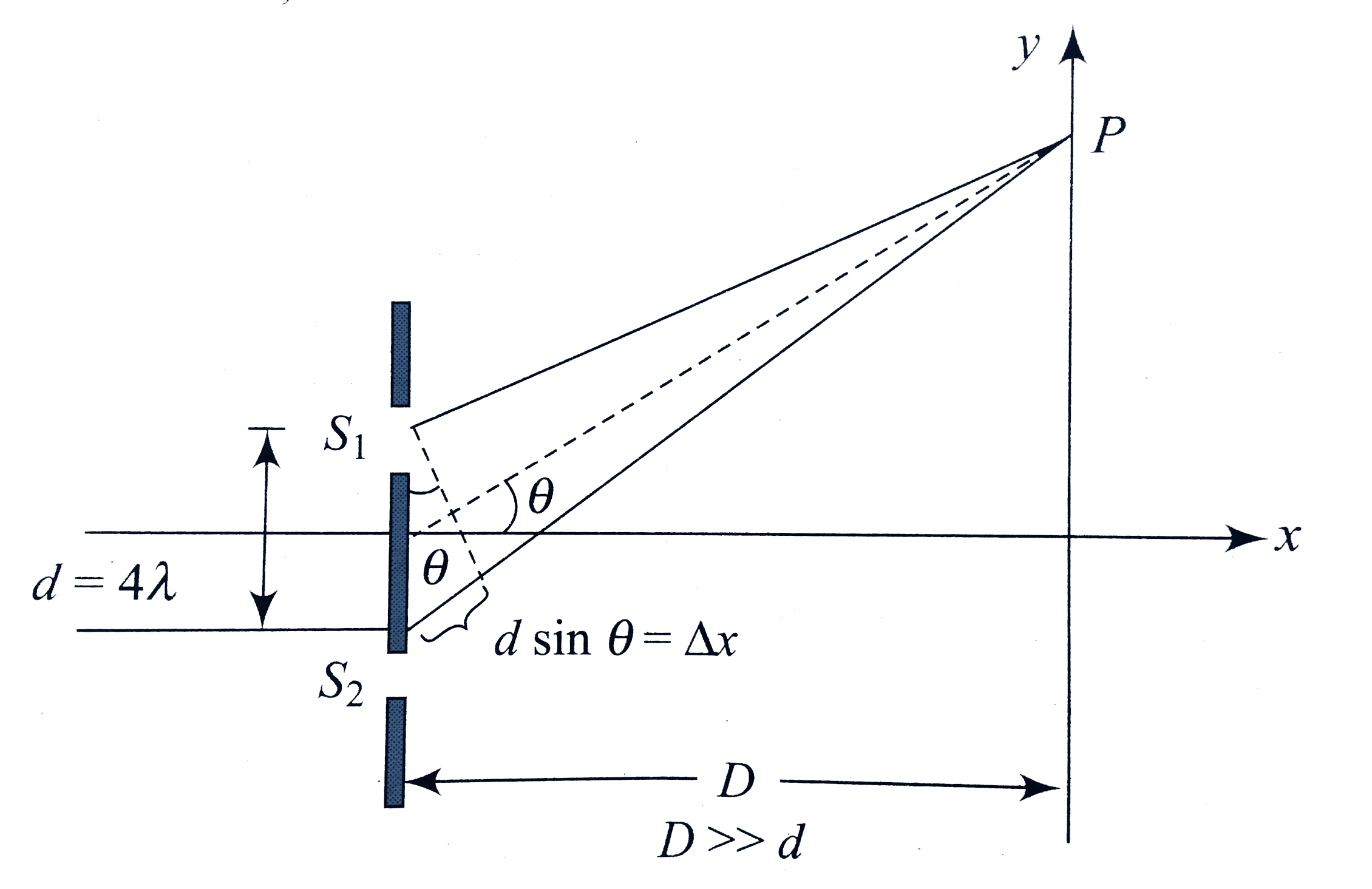
If a detector moves along the y-axis, what is the maximum number of minima observed?View SolutionTwo identical coherent sources are placed on a diameter of a circle of radius R at separation x (<<R) symmetrical about the center of the circle. The sources emit identical wavelength λ each. The number of points on the circle of maximum intensity is (x=5λ)
View SolutionTwo coherent point sources S1 and S2 vibrating in phase light of wavelength λ. The separation between the sources is 2λ. The smallest distance from S2 on a line passing through S2 and perpendicular to s1s2 where a minimum of intensity occurs is
View SolutionTwo coherent light sources S1 and S2(λ=6000Å) are 1mm apart from each other. The screen is placed at a distance of 25cm from the sources. The width of the fringes on the screen should be
View SolutionS1 and S2 in List I represent coherent point sources, S represents a point source λ = wavelength of light emitted by the sources. Fringe pattern is observed on the screen. Exclude the position of source while detecting the fringe pattern.
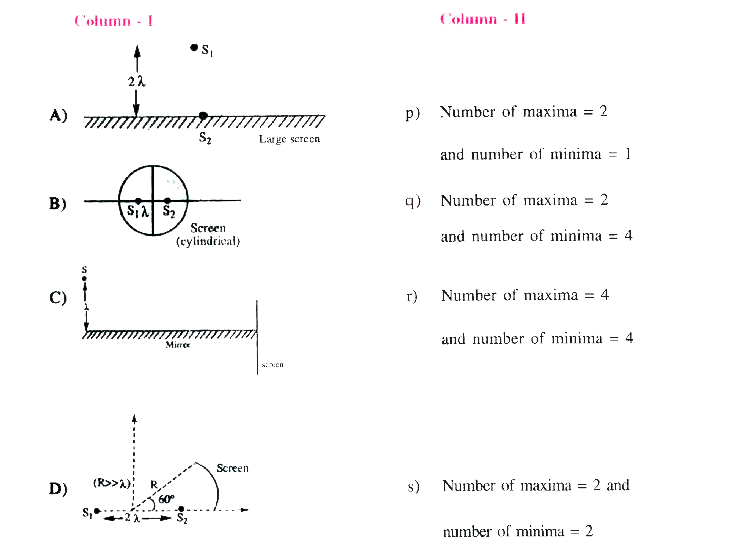 View Solution
View Solution

