Two particles P and Q are located ar distance rp and rq respectively from the axis of a rotating disc such that rp>rq
Both P and Q have the same acceleration
Both P and Q do not have any acceleration
P has greater acceleration that Q
Q has greater acceleration that P
The correct Answer is:C
Topper's Solved these Questions
Similar Questions
Knowledge Check
Two particles P and Q are located at distance rpandrQ respectively form the centre of rotating disc such that rP>rQ. The disc is rotating with constant angular acceleration. We can say
ABoth P and Q have the same acceelerationBBoth P and Q do not have any accelcrationCP has greater acceleration than QDQ has greater acceleration than PTwo particles p and q located at distances rp and rq respectively from the centre of a rotating disc such that rp>rq.
Aboth p and q have the same accelerationBboth p and q do not have any accelerationCp has greater acceleration then qDq has greater acceleration than pTwo particles P and Q are located at distance rpandrQ respectively form the centre of rotating disc such that rP>rQ. The disc is rotating with constant angular acceleration. We can say
Aboth P and Q have the same accelerationBboth P and Q do not have the same accelerationCP has greater acceleration than QDQ has greater acceleration than P
sides QP and RQ of PQR are produced to point S and T respectively. If ∠SPR=1350 and ∠PQT=1100, find ∠PRQ.
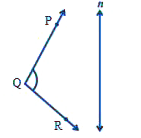
View SolutionDraw the images P' , Q' and R' of the point P, Q and R respectively in the line n (Fig . 9. 18). Join P' Q' and Q' R' to form an angle P' Q' R' Measure ∠PQRand∠P'Q'R' . Are the two angles equal ?
View SolutionTwo loops P and Q are made from a uniform wire. The radii of P and Q are R1andR2 respectively and their moments of inertia are IPandIQ respectively.
If IPIQ=8 then R1R2 is
View SolutionIf p,q and r are perpendicular to q + r , r + p and p + q respectively and if |p+q|=6,|q+r|=4√3andabs(r+p) = 4then|p+q+r| is
View SolutionIf p, q and r are perpendicular to q + r, r + p and p + q respectively and if |p + q| = 6, |q + r| = 4√3 and |r + p| = 4, then |p + q + r| is
View Solution
