Two identical charged particles are fastened to the two ends of a spring of stiffness 100 N/m and natural length 10 cm. The system rests on a smooth horizontal table. If the charge on each particle is 2×10−8C, find the extension in the length of the spring, when the system is in equilibrium assume that extension is small as compared to the natural length.Solution in Bengali
Step by step video & image solution for Two identical charged particles are fastened to the two ends of a spring of stiffness 100 N/m and natural length 10 cm. The system rests on a smooth horizontal table. If the charge on each particle is 2times10^(-8)C, find the extension in the length of the spring, when the system is in equilibrium assume that extension is small as compared to the natural length. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBOOK - PATHFINDERCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - QUESTION BANK
50 Videos
- MAGNETIC EFFECT OF CURRENT AND ELECTROMAGNETISM-I,II AND IIIBOOK - PATHFINDERCHAPTER - MAGNETIC EFFECT OF CURRENT AND ELECTROMAGNETISM-I,II AND IIIEXERCISE - QUESTION BANK
213 Videos
Similar Questions
Can two equipotential surfaces intersect?
View SolutionA wire placed along north south direction carries a current of 10A from south to north find the magnetic field due to a 1 cm piece of wire at a point 200cm north east from the piece
View SolutionTwo charged particles having charge 2.0×10−8C each are joined by an insulating string of length 1 m and the system is kept on a smooth horizontal table. Find the tension in the string.
View SolutionTwo identically charged particles are fastened to the two ends of a spring of spring constant 100Nm−8C, find the extension In the length of the apring. Assume that the extension is small as scompared to the natural length . Justify this assumption after you solve the problem.
View SolutionTwo identical blocks A and B , each of mass m resting on smooth floor are connected by a light spring of natural length L and spring constant k , with the spring at its natural length. A third identical block C (mass m ) moving with a speed v along the line joining A and B collides with A . The maximum compression in the spring is
View SolutionThe system is released from rest with spring intially in its natural length. If mass of the block m = 10 kg. and spring constant k = 100 N//m , then maximum extension in spring is :
View SolutionIf the system is suspended by the mass m the length of the spring is l1. If it is inverted and hung by mass M, the length of the spring is l2. Find the natural length of the spring.

View SolutionTwo bolcks A & B are connected by a spring of stiffness 512N/m and placed on a smooth horizontal surface. Initially the spring has its equilibrium length. The indicated velocities are imparted to A & B. Find the maximum extension in the spring?
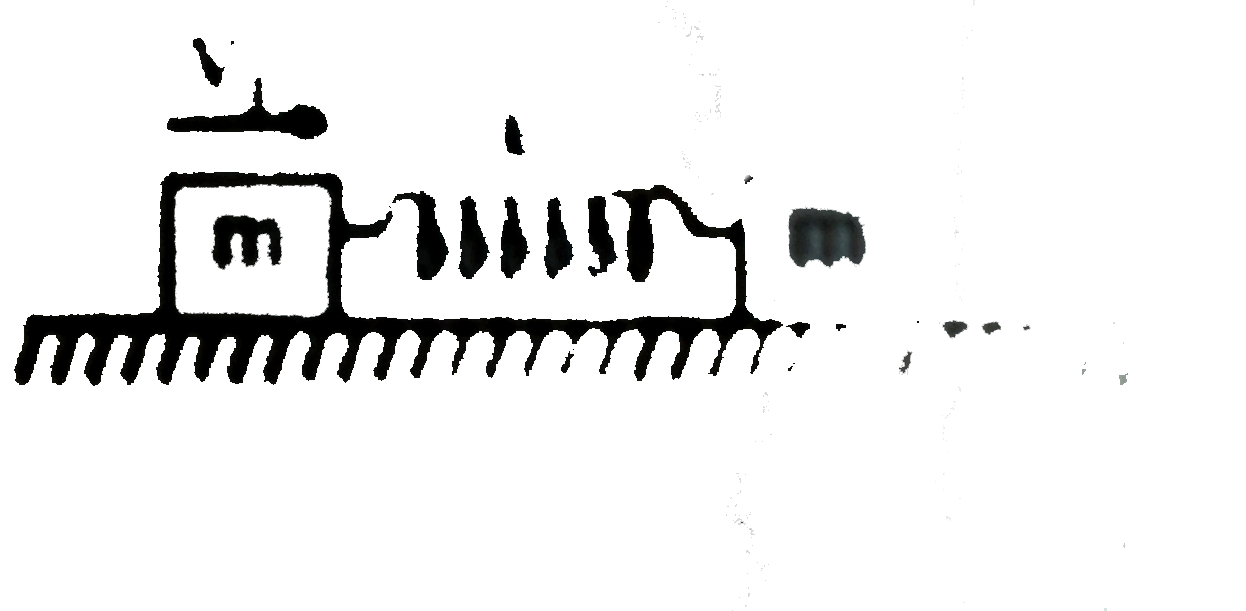
View SolutionIn the situations shown in the figure surfaces are frictionless. Find the maximum extension of the springs if blocks are initially at rest and springs are initially in natural lengths.

View SolutionA particle of mass 'm' attached with one end of a light spring of stiffness (k) is pushed with a speed (v) on a smooth horizontal plane. If l0= natural length of the spring and x0 = elongation of the spring at the given instant.
View SolutionTwo charged particles having charge 2.0×10−8C each are joined by an insulating string of length 1 m and the system is kept on a smooth horizontal table. Find the tension in the string.
View SolutionTwo identically charged particles are fastened to the two ends of a spring of spring constant 100Nm−1, find the extension In the length of the spring. Assume that the extension is small as compared to the natural length . Justify this assumption after you solve the problem.
View SolutionTwo indentical particles of charge q each are connected by a less spring of force constant K. They are placed over a smooth horizontal surface. They are released when the separation between them is r and spring is in it natural length. If maximum extension of the spring is r, the value of K is (neglect gravitational effect)
View SolutionTwo identical blocks A and B , each of mass m resting on smooth floor are connected by a light spring of natural length L and spring constant k, with the spring at its natural length. A third identical block C (mass m) moving with a speed v along the line joining A and B collides with A. The maximum compression in the spring is
View SolutionTwo blocks A and B. each of mass m, are connected by a massless spring of natural length I. and spring constant K. The blocks are initially resting in a smooth horizontal floor with the spring at its natural length, as shown in Fig. A third identical block C, also of mass m, moves on the floor with a speed v along the line joining A and B. and collides elastically with A. Then

View Solution
