→OA and →BO are two vectors of magnitudes 5 and 6 respectively.If ∠(BOA)=60∘, then −−→OA.−−→OB is equal toSolution in Kannada
15
2
15√3
minus 15
The correct Answer is:A
Step by step video, text & image solution for vec OA and vec BO are two vectors of magnitudes 5 and 6 respectively.If angle (BOA) = 60^(@), then vec (OA) .vec(OB) is equal to by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
The direction cosines of the line making angles 45o,30o and 120o with the coordinate axes are
View SolutionIf the projection of Vector vec OA on unit vector vec OB equals twice the area of Delta OAB in magnitude,then /_AOB is
View SolutionThe magnitudes of vectors vec OA,vec OB and vec OC( in figure( 2-W3) are equal.Find the direction of )/(Ovec A)+vec OB-vec OC.
View SolutionFind the resultant of the three vectors vec OA,vec OB and vec OC each of magnitude r as shown in figure?
View SolutionIf −−→OA=2ˆi+3ˆj−4ˆkand−−→OB=ˆj+ˆk are two vectors through the origin O, find the projection of −−→OAand−−→OB
View SolutionIf −−→OA=2ˆi+3ˆj−4ˆkand−−→OB=ˆj+ˆk are two vectors through the origin O, find the projection of −−→OBon−−→OA.
View SolutionThe magnitude of vectors −−→OA,−−→OBand−−→OC in figure are equal. Find the direction of −−→OA+−−→OB−−−→OC.
 .
.
View SolutionThe resultant of vectors −−→OAand−−→OB is peerpendicular to vec(OA). Find the angle AOB.
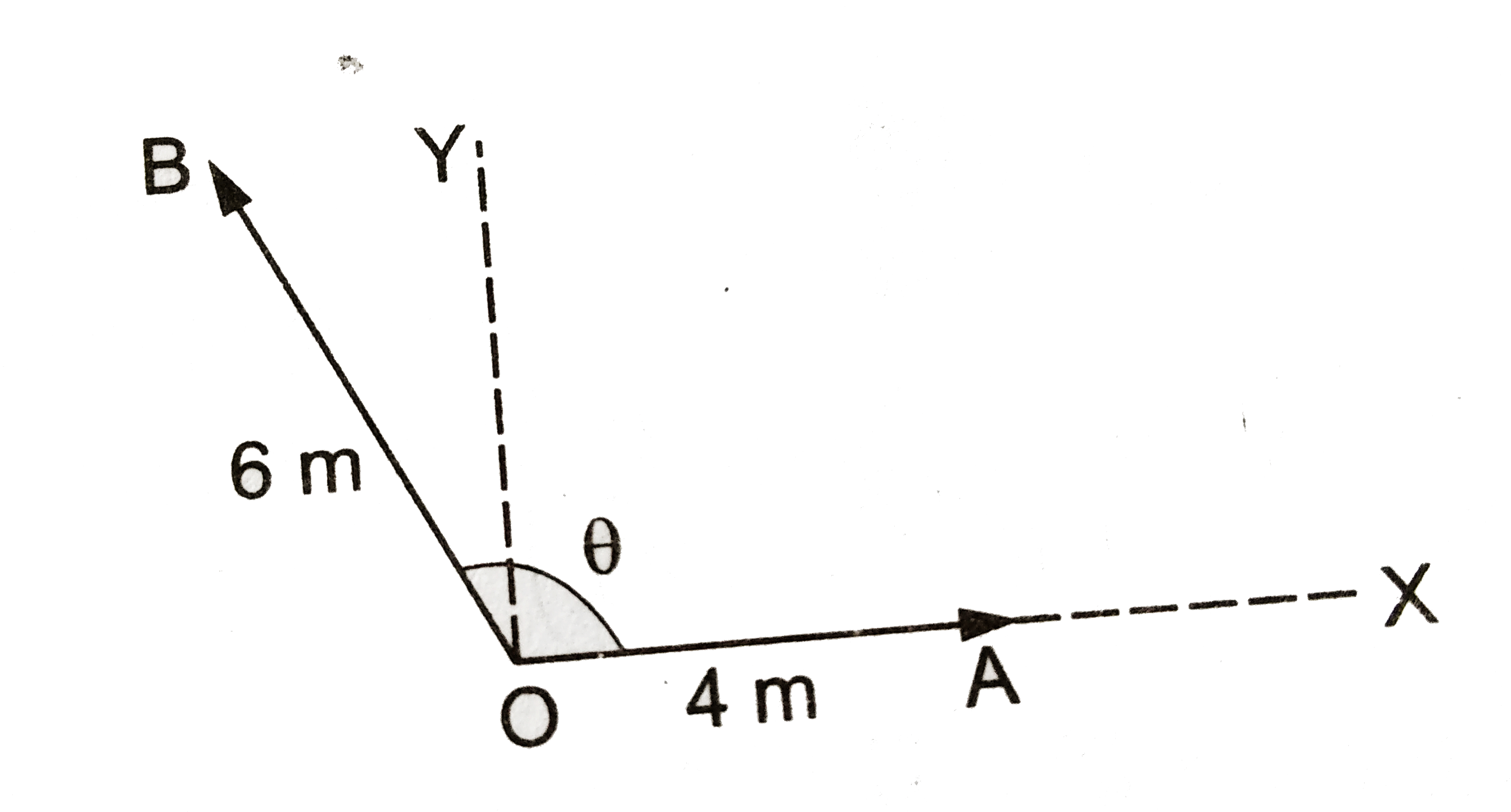
View Solutionदिखाए गए वेक्टरो −−→OA,−−→OB तथा −−→OC के परिमाण बराबर है। वेक्टर −−→OA+−−→OB−−−→OC की दिशा बताएँ।
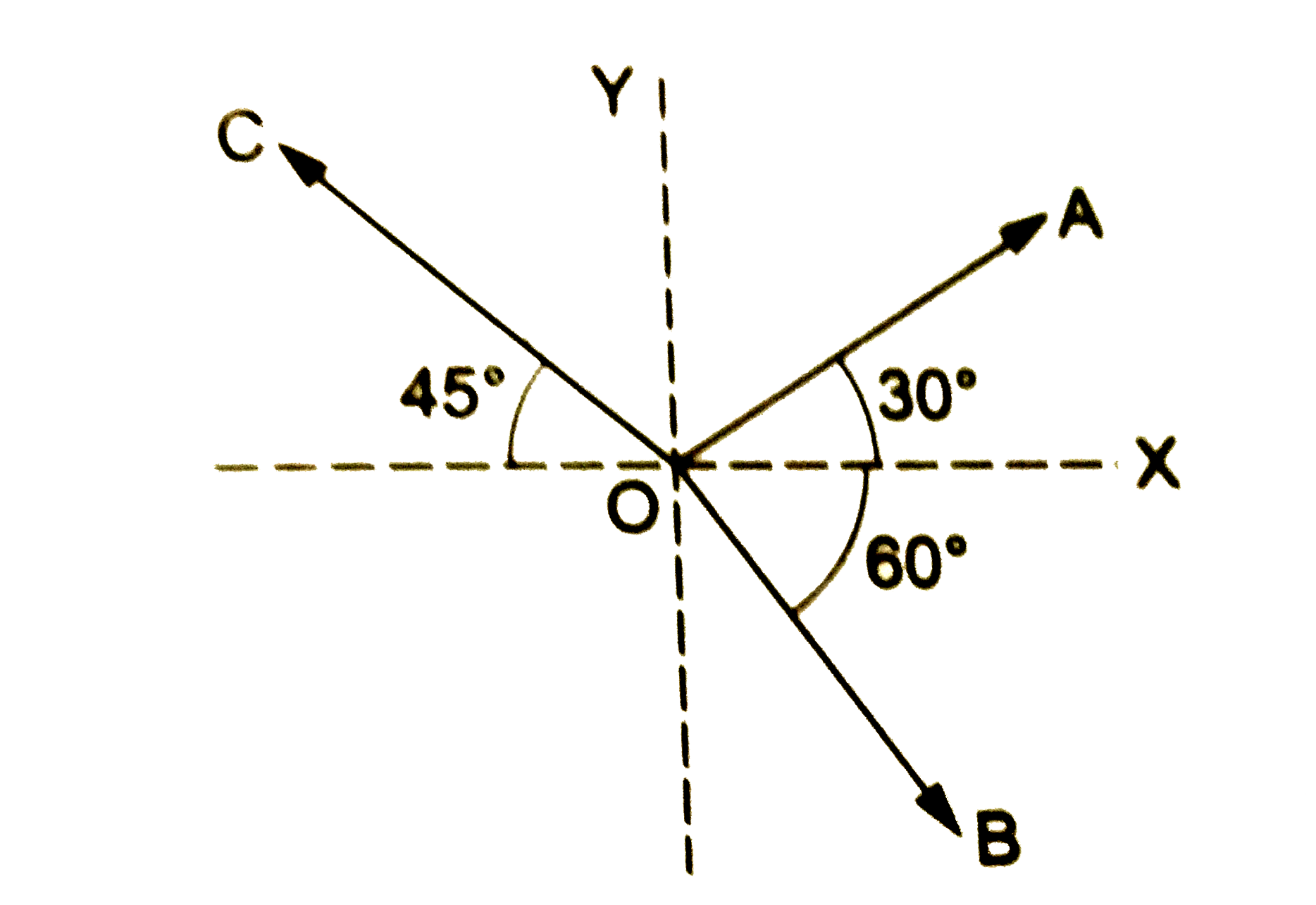
View SolutionIf OAB is a tetrahedron with edges and ˆp,ˆq,ˆr are unit vectors along bisectors of
−−→OA,−−→OB:−−→OB,−−→OC:−−→OC,−−→OA respectively and ˆa=−−→OA∣∣∣−−→OA∣∣∣,→b=−−→OB∣∣∣−−→OB∣∣∣,→c=−−→OC∣∣∣−−→OC∣∣∣, then :
View SolutionIf OAB is a tetrahedron with edges and ˆp,ˆq,ˆr are unit vectors along bisectors of
−−→OA,−−→OB:−−→OB,−−→OC:−−→OC,−−→OA respectively and ˆa=−−→OA∣∣∣−−→OA∣∣∣,→b=−−→OB∣∣∣−−→OB∣∣∣,→c=−−→OC∣∣∣−−→OC∣∣∣, then :
View Solution→OA and →BO are two vectors of magnitudes 5 and 6 respectively.If ∠(BOA)=60∘, then −−→OA.−−→OB is equal to
View SolutionThe magnitude of vectors −−→OA,−−→OBand−−→OC in figure are equal. Find the direction of −−→OA+−−→OB−−−→OC.
 .
.
View SolutionThe resultant of vectors −−→OAand−−→OB is perpendicular to −−→OA. Find the angle AOB.

View Solution−−→OAand−−→BO are two vectors of magnitudes 5 and 6 respectively. If ∠BOA=60∘,then −−→OA.−−→OB is equal to
View SolutionThe resultant of vectors −−→OAand−−→OB is peerpendicular to −−→OA. Find the angle AOB.

View Solution
