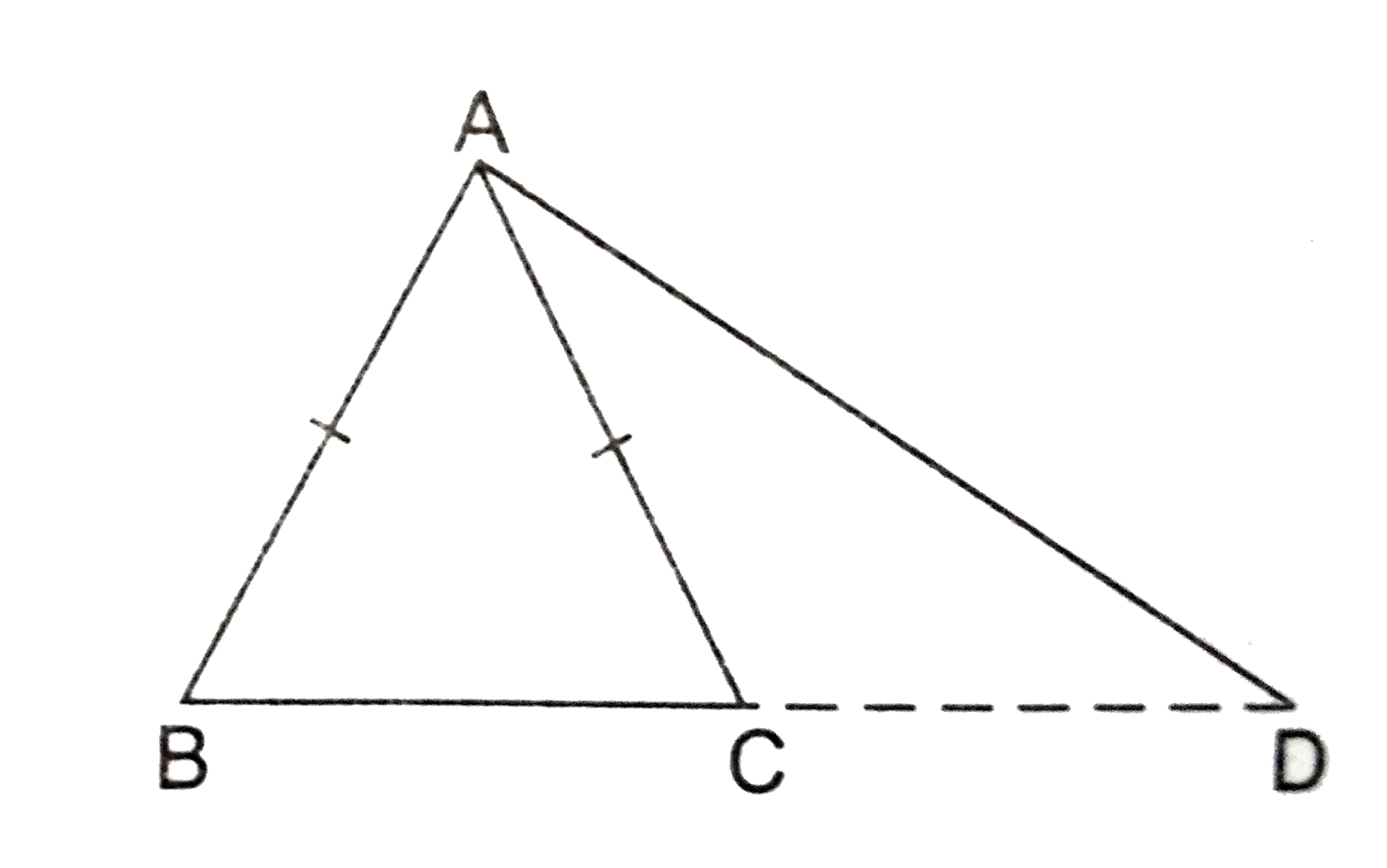
The perpendicular from C on the side AB of a triangle ABC intersect AB at D and BD=mAD. Prove that (m+1)BC2=(m+1)AC2+(m−1)AB2.Solution in Assamese
Step by step video & image solution for The perpendicular from C on the side AB of a triangle ABC intersect AB at D and BD=mAD. Prove that (m+1)BC^2=(m+1)AC^2+(m-1)AB^2. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Topper's Solved these Questions
Similar Questions
The length of a diagonal of a square is 16cm. Find the length of the side of it.
03:13View Solutiona number is selected from 1,2,3,....,15. what is the probability that the number is a multiple of 4
03:37View SolutionWhich of the following is quadratic equation:
x2+√2x+3=0.02:03View SolutionABC is an isosceles triangle with AB=AC and D is a point on AC such that BC2=ACxCD. Prove that BD=BC
05:10View SolutionABC is a triangle in which AB=AC and D is a point on AC such that BC^(2)=AC xx CD .Prove that BD=BC .
02:56View SolutionIn an isosceles triangle ABC with AB=AC , BD is perpendicular from B to the side AC . Prove that BD2−CD2=2 CDAD
04:41View SolutionIn an isoscles ΔABC,AB=ACandD is a point on BC. Prove that AB2−AD2=BD⋅CD.
03:50View SolutionIn ΔABC,AB=AC. Side BC is produced to D. Prove that (AD2−AC2)=BD⋅CD.
 01:32View Solution
01:32View Solutionएक समद्विभाहु त्रिभुज ABC में भुजा AB = भुजा AC तथा बिंदु B से भुजा AC पर BD लम्ब है । सिद्ध कीजिए कि BC2=2AC.DC.
02:56View Solutionयदि ΔABC की भुजा BC का मध्य बिन्दु D है तब सिद्ध कीजिये कि
AB2+AC2=2(AD2+BD2)02:33View Solutionएक त्रिभुज ABC है | जिसमे AB = AC तथा D, BC पर कोई बिंदु है | तो सिद्ध कीजिए कि
AB2−AD2=BD⋅CD03:08View Solutionएक △ABC में, AB = AC तथा D, AC का मध्य बिंदु है और BC2=AC×CD हो तो सिद्ध कीजिए कि BD = BC
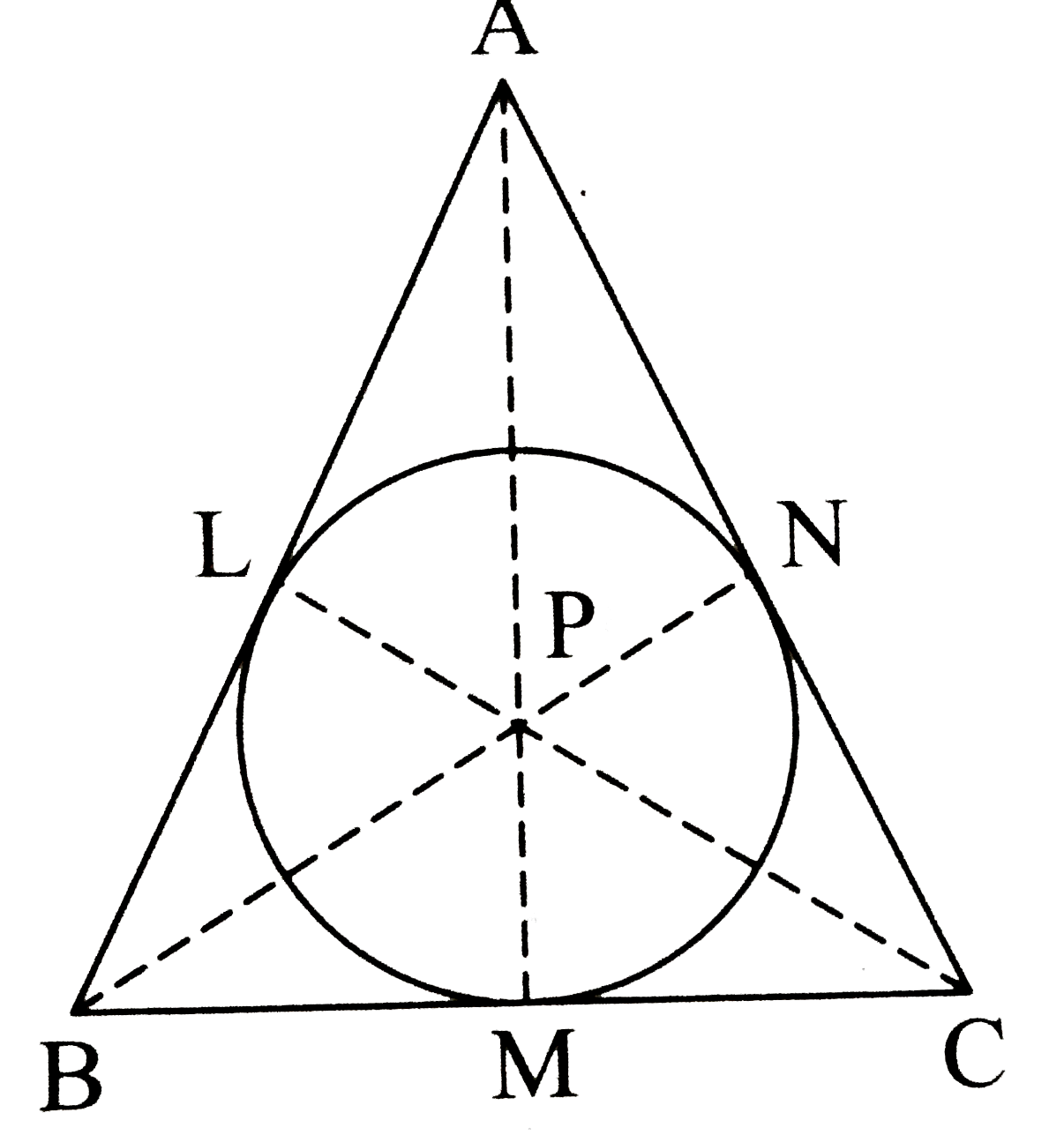
05:30View SolutionA circle with centre P is inscribed in the ΔABC Side AB, side BC and side A C touch the circle at points L,M and N respectively . Prove that :
A(ΔABC)=12(AB+BC+AC)×r
 03:36View Solution
03:36View SolutionThe perpendicular from A on side BC at a ΔABC intersects BC at D such that DB=3 CD. Prove that 2AB2=2AC2+BC2
05:27View SolutionABC is a right angle in a right triangle ABC. Prove the following if the line drawn parallel to BC through the midpoint M of hypotenuse AB intersects AC at D. CM=MA = 1/2 AB
05:56View SolutionIn ΔABC, BD:CD=3:1 and AD⊥BC. Prove that 2(AB2−AC2)=BC2.
05:35View Solution

