ΔPQR is right angled at Q and the points S and T trisect the side QR. Prove that 8PT2=3PR2+5PS2.Solution in Assamese
Step by step video & image solution for ∆PQR is right angled at Q and the points S and T trisect the side QR. Prove that 8PT^2 = 3PR^2 + 5PS^2. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
The length of a diagonal of a square is 16cm. Find the length of the side of it.
View Solutiona number is selected from 1,2,3,....,15. what is the probability that the number is a multiple of 4
View SolutionWhich of the following is quadratic equation:
x2+√2x+3=0.
View SolutionIn Fig. 6.44, the side QR of PQR is produced to a point S. If the bisectors of ∠PQR and ∠PRS meet at point T, then prove that ∠QTR=12∠QPR.

View Solution1. In the figure trianglePQR is an equilateral triangle, the point N is on ray QR such that QR=RN. Prove that PN^2 = 3PR^2
View SolutionM and N are the points on sides QR and PQ respectively of a △PQR, right angled at Q. prove that PM2+RN2=PR2+MN2
View SolutionIn the figure given below, ΔPQR is right-angled at Q and the points S and T trisect the side QR. Prove that 8PT2=3PR2+5PS2
View SolutionIn the figure , M is the midpoint of QR .
∠PRQ=90∘.
Prove that ,
PQ2=4PM2−3PR2 .
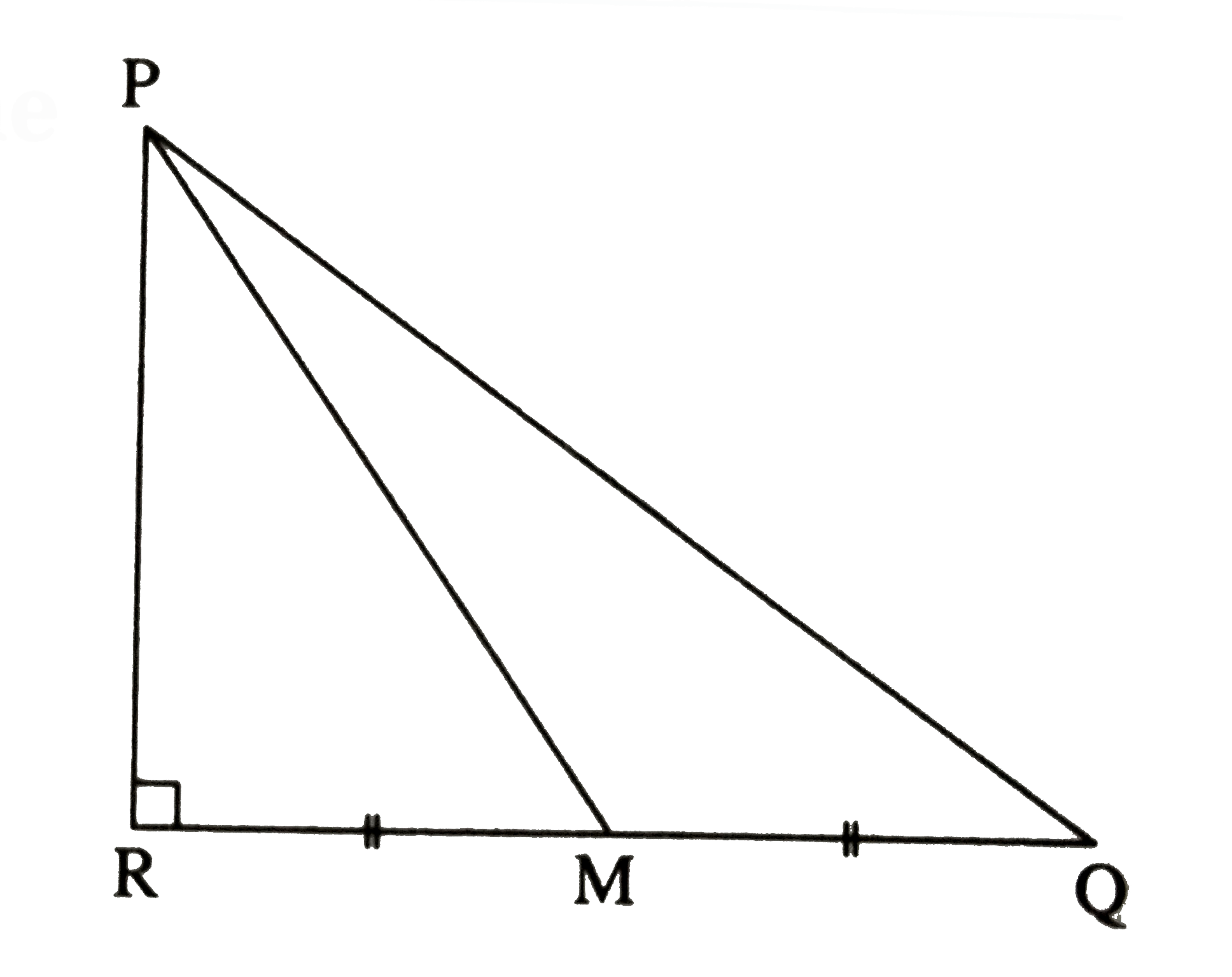
View SolutionPQR is a triangle whose ∠Q is right angle. If S is any point on QR, then prove that PS2+QR2=PR2+QS2
View Solutionदिए चित्र में ΔPQR में ∠Q समकोण है तथा S और T , QR को समत्रिभाजित करते है सिद्ध कीजिये कि 8PT2=3PR2+5.PS2

View SolutionIn an isosceles triangle PQR, PQ =PR and S is any point on side QR. Then prove that: PQ2−PS2=QS×SR.
View SolutionIn the adjoining figure , Delta PQR is an equilateral triangle. QR = RN . Prove that PN^(2) =3PR^(2)
View SolutionIn the adjoining figure, angle PQR = 90^(@)T is the midpoint of side QR. Prove that PR^(2) = 4PT^(2) - 3PQ^(2)
View SolutionIn Fig. , the side QR of △ PQR is produced to a point S. If the bisectors of ∠PQR and ∠PRS meet at point T, then prove that ∠QTR=12∠QPR.

View SolutionIn an isosceles triangle PQR, PQ =PR and S is any point on side QR. Then prove that: PQ2−PS2=QS×SR.
View Solution
