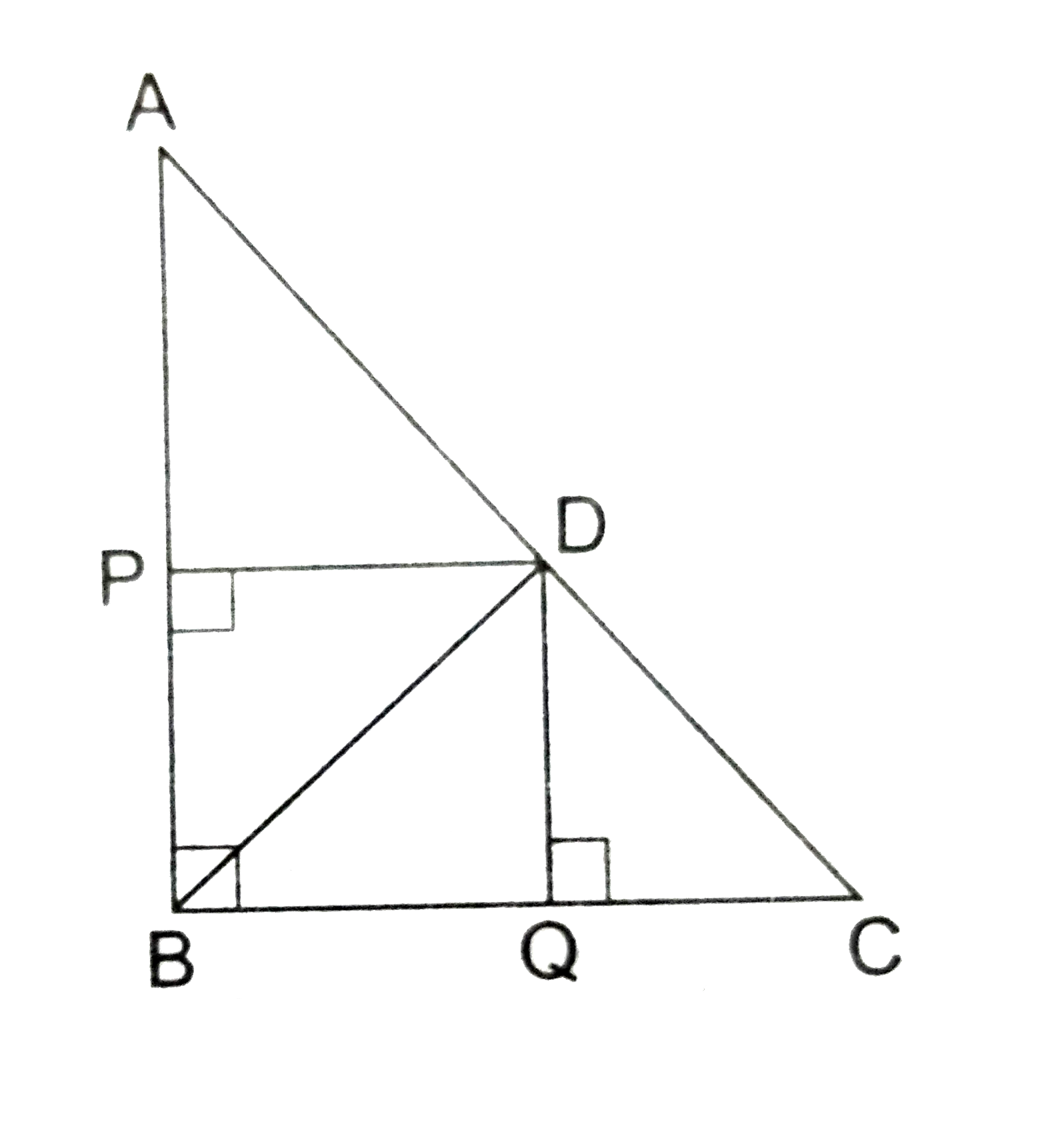
ABC and DBC are two right angled triangles with common hypotenuse BC with their sides AC and BD intersecting at P. Prove that:
AP×PC=DP×PB. Solution in Assamese
Step by step video & image solution for ABC and DBC are two right angled triangles with common hypotenuse BC with their sides AC and BD intersecting at P. Prove that: AP×PC=DP×PB. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Express sinθ, cosθ,cotθin terms of secθ .
View SolutionIf the mean of the following data is 18.75,find the value of p.

View SolutionIn a right tringle ABC, right-angled at B, D is a point on hypotenuse such that BD⊥AC. If DP⊥ABandDQ⊥BC then prove that
(a)DQ2=DP⋅QC DP2=DQ⋅AP.
View Solutionउभयनिष्ट कर्ण AC वाले दो समकोण त्रिभुज ABC और ADC है । सिद्ध कीजिए कि ∠CAD=∠CBD है।
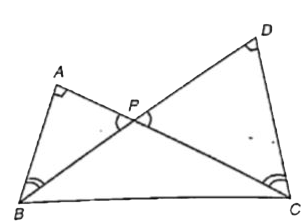
View Solutionचित्र में , उभयनिष्ट विकर्ण BC के दो समकोण त्रिभुज ABC तथा DBC हैं तथा भुजाएँ AC तथा DB एक - दूसरे को एक बिन्दु P पर प्रतिच्छेद करती हैं । सिद्ध कीजिए कि AP.PC=DP.PB.
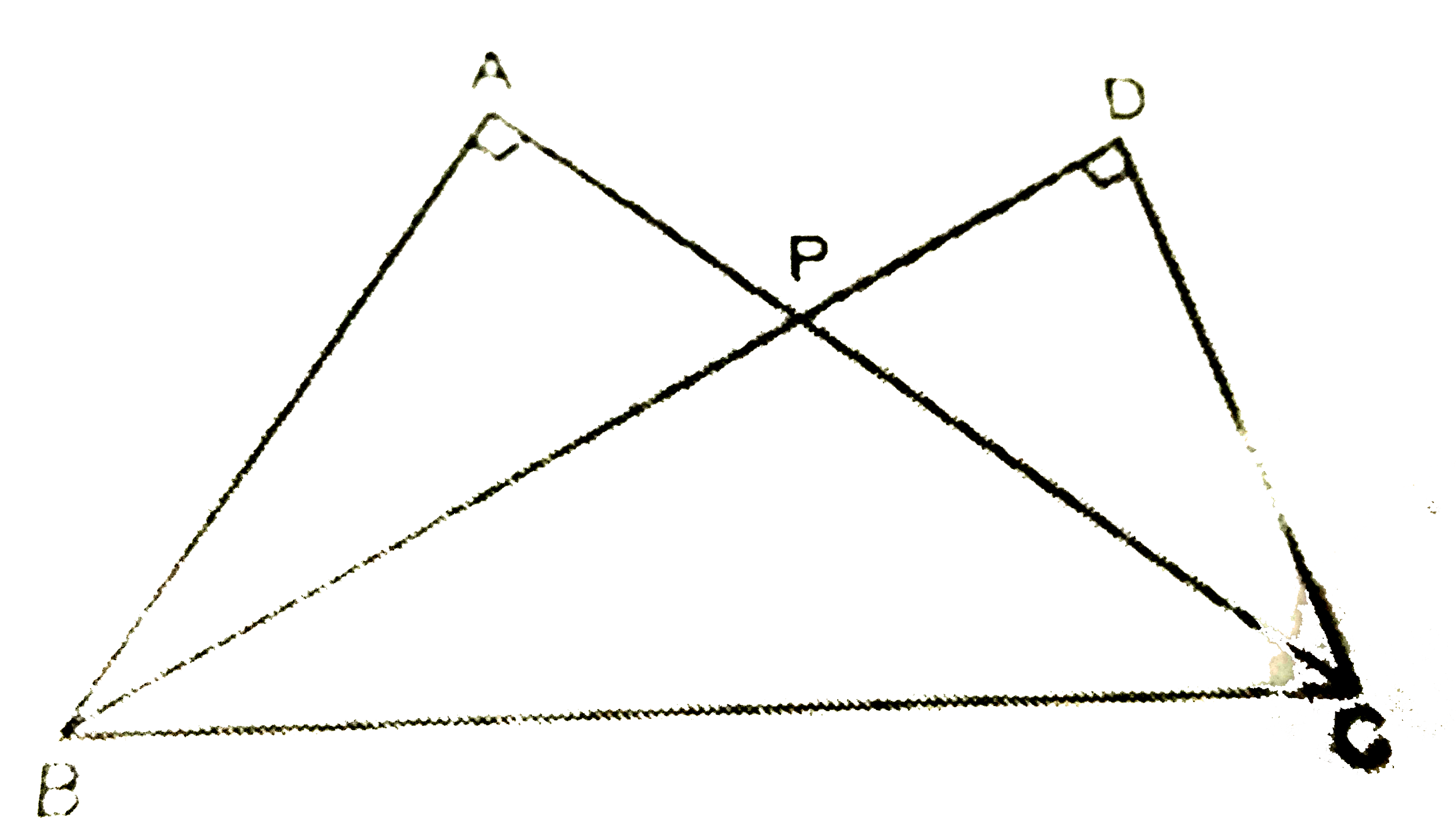
View Solutionउभयनिष्ठ कर्ण AC वाले दो समकोण त्रिभुज ABC और ADC है, सिध्द कीजिए कि ∠CAD=∠CBD है।
View Solutionएक ही कर्ण BC पर एक ही तरफ दो समकोण त्रिभुज ABC और DBC खींचे गये है । यदि AC और BD , एक -दूसरे को P पर प्रतिच्छेद करते है , तो सिद्ध करें कि AP×PO=BP×PD
View SolutionABC और DBC दो त्रिभुज एकही आधार BC पर विपरीत पार्शव में है । यदि AD,BC को P पर प्रतिच्छेद करती है
तो दिखाएँ कि ar(ΔABC)ar(DBC)=APDP
View SolutionABC and DBC are two triangle on the same base BC such that A and D lie on the opposite sides of BC, AB=BD and /_ ABC =/_ DBC then
View Solutionसमकोण त्रिभुज ABC क़ि भुजा AB को व्यास मानकर खींचा गया वृत्त कर्ण AC को P पर प्रतिच्छेद करता है सिद्ध कीजिये क़ि बिंदु P पर वृत्त क़ि स्पर्श रेखा भुजा BC को समद्विभाजित करती है।
View SolutionTwo right triangles ABC and DBC are drawn on the same hypotenues BC on the same side of BC. If AC and DB intersects at P, then :
View SolutionIn a right triangle ABC, a circle with a side. AB as diameter is drawn to intersect the hypotenuse AC in P. Prove that the tangent to the circle at P bisects the side BC.
View SolutionIn a right triangle ABC, a circle with a side. AB as diameter is drawn to intersect the hypotenuse AC in P. Prove that the tangent to the circle at P bisects the side BC.
View SolutionABC and ADC are two right triangles with common hypotenuse AC. Prove that ∠CAD=∠CBD.
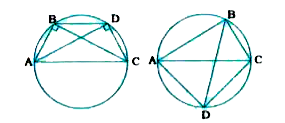
View SolutionConstruct a right-angled triangled right-angled at A, hypotenuse BC = 6.5 cm and AB = 5 cm. Construct the perpendicular bisectors of AB and AC. Mark the point of intersection of the perpendicular bisectors as P. Measure PA, PB and PC.
View Solution
