At point 'P' on a circle, PQ is a tangent and 'O' is the centre of the circle. If △OPQ is an isosceles triangle, then ∠OQP is equal toSolution in Telugu
90∘
30∘
45∘
60∘
Step by step video & image solution for At point 'P' on a circle, PQ is a tangent and 'O' is the centre of the circle. If triangleOPQ is an isosceles triangle, then /_OQP is equal to by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Topper's Solved these Questions
Similar Questions
The mean value can be calculated from both ungrouped and grouped date . Which one you think is more accurate ? Why ?
03:20View SolutionA tangent PQ at a point P of a circle of radius 5 cm meets a line through the centre O at a point Q so that OQ = 12cm . Find length of PQ .
01:18View SolutionIf the tangent at a point P to a circle with centre O cuts a line through O at Q such that PQ=24cm and OQ=25cm . Find the radius of the circle.
02:02View SolutionPQ is a tangent to a circle with centre O at the point P . If OPQ is an isosceles triangle, then ∠OQP is equal to 30o (b) 45o (c) 60o (d) 90o
00:49View SolutionPQ वृत्त के बिन्दु P पर वृत्त की स्पर्श रेखा हैं। वृत्त का केन्द्र O हैं। यदि ΔOPQ एक समद्विबाहु त्रिभुज हैं तो ∠QOP हैं-
02:37View SolutionPQ is a tangent to a circle with centre O at the point P. If ΔOPQ is an isoceless triangle, then ∠OQP is equal to
03:53View Solutionचित्र में, O वृत्त का केन्द्र है। बिन्दु Q से वृत्त के बिन्दु P पर स्पर्शी PQ इस प्रकार है कि PQ = 4 सेमी तथा ∠PQO=45∘ | वृत्त कि त्रिज्या ज्ञात कीजिए ।
 05:13View Solution
05:13View SolutionO केंद्र वाली वृत्त के बिंदु P पर PQ स्पर्श रेखा हैं। यदि △OPQ एक समद्विबाहु त्रिभुज हो, तब ∠OQP बराबर हैं।
05:42View SolutionPoint O is the centre of a circle . Line a and line b are parallel tangents to the circle at P and Q. Prove that segment PQ is a diameter of the circle.
 05:09View Solution
05:09View SolutionIf two tangents are inclined at 60∘ are drawn to a circle of radius 3cm then find length of each tangent.
OR
PQ is a tangent to a circle with centre O at point P. If ΔOPQ is an isosceles triangle, then find ∠OQP.03:02View SolutionIn figure, if O is the centre of a circle, PQ is a chord and the tangent PR at P makes an angle of 50∘ with PQ, then ∠POQ is equal to
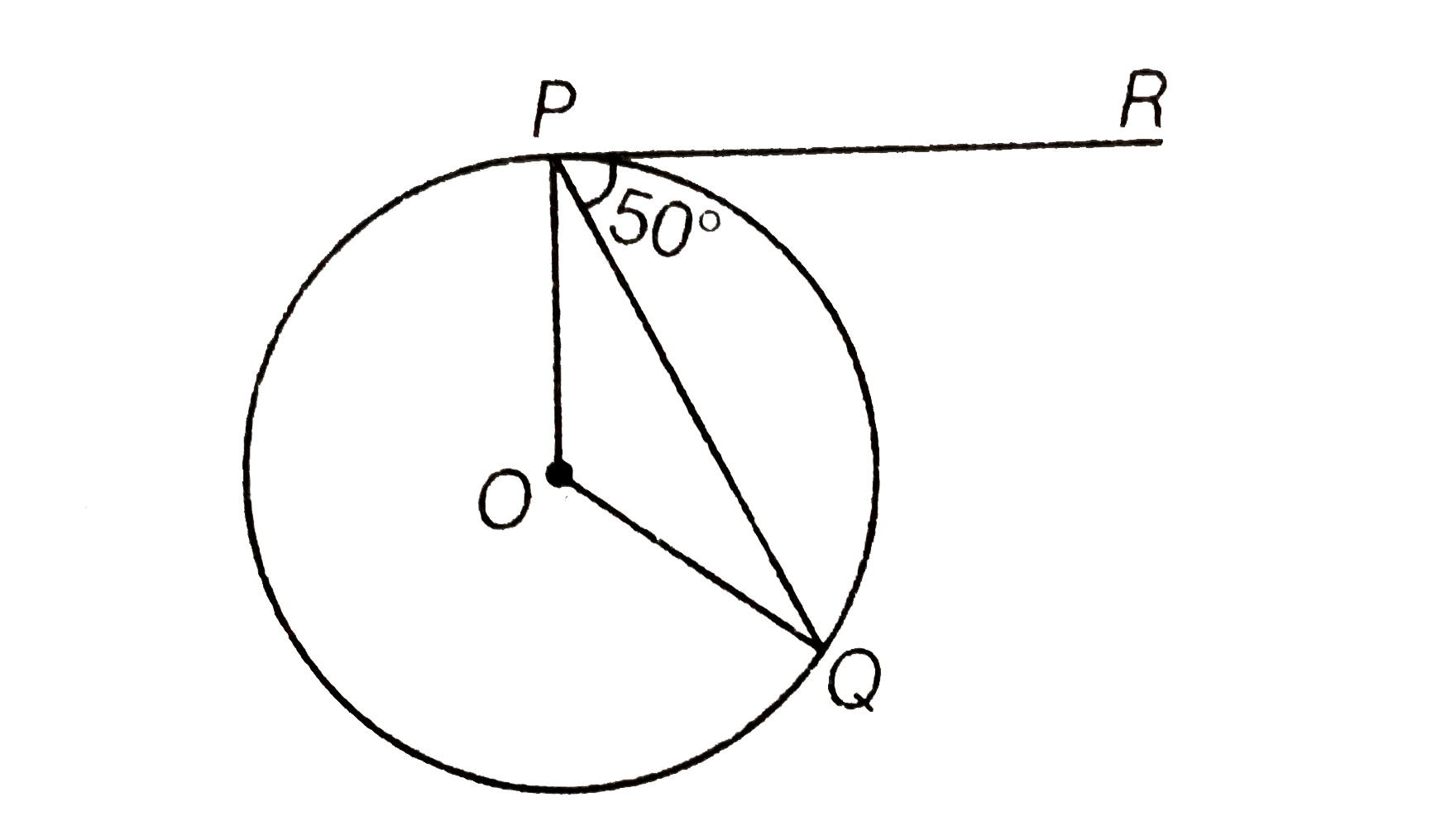 04:24View Solution
04:24View SolutionPQ is a tangent to a circle with centre O at the point P . If △OPQ is an isosceles triangle, then ∠OQP is equal to :
03:02View SolutionPoint O is the centre of a circle . Line a and line b are
parallel tangents to the circle at P and Q. Prove that
segment PQ is a diameter of the circle.
 02:20View Solution
02:20View SolutionLine PQ is a tangent to the circle at point A, arcAB≅arcAC. Prove that △ABC is isosceles triangle.
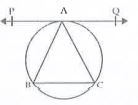 02:58View Solution
02:58View SolutionPQ is a tangent to a circle with centre O at the point P. If ΔOPQ is an isosceles triangle, then ∠OQP=………..
02:12View Solution

