The ratio of velocity of two objects A and B is 1:3. It the position-time graph of object A is inclined to time axis at 30∘, then the position-time graph of object B is inclined to time axis at
A. 0∘
B. 90∘
C. 30∘
D. 60∘
0∘
90∘
30∘
60∘
The correct Answer is:D
To solve the problem, we need to analyze the information given about the two objects A and B, particularly focusing on their velocities and the angles of their position-time graphs.
1. Understanding the Given Ratio of Velocities:
The ratio of the velocities of objects A and B is given as vA:vB=1:3. This means that if the velocity of object A is vA, then the velocity of object B is vB=3vA.
2. Analyzing the Position-Time Graph of Object A:
The position-time graph of object A is inclined to the time axis at an angle of 30∘. The slope of a position-time graph gives us the velocity of the object. Therefore, we can express the velocity of object A in terms of the angle:
vA=tan(30∘)
3. Calculating tan(30∘):
The value of tan(30∘) is known:
tan(30∘)=1√3
Thus, we have:
vA=1√3
4. Finding the Velocity of Object B:
Since vB=3vA, we can substitute the value of vA:
vB=3×1√3=3√3=√3
5. Relating the Angles of the Position-Time Graphs:
Let the angle of inclination of the position-time graph of object B be θ. The velocity of object B can also be expressed in terms of this angle:
vB=tan(θ)
6. Setting Up the Equation:
From the velocities we have:
tan(θ)=√3
7. Finding the Angle θ:
We know that:
tan(60∘)=√3
Therefore, we can conclude:
θ=60∘
8. Final Answer:
The angle at which the position-time graph of object B is inclined to the time axis is 60∘.
Conclusion:
The correct answer is D. 60∘.
The ratio of the velocities of objects A and B is given as vA:vB=1:3. This means that if the velocity of object A is vA, then the velocity of object B is vB=3vA.
The position-time graph of object A is inclined to the time axis at an angle of 30∘. The slope of a position-time graph gives us the velocity of the object. Therefore, we can express the velocity of object A in terms of the angle:
vA=tan(30∘)
The value of tan(30∘) is known:
tan(30∘)=1√3
Thus, we have:
vA=1√3
Since vB=3vA, we can substitute the value of vA:
vB=3×1√3=3√3=√3
Let the angle of inclination of the position-time graph of object B be θ. The velocity of object B can also be expressed in terms of this angle:
vB=tan(θ)
From the velocities we have:
tan(θ)=√3
We know that:
tan(60∘)=√3
Therefore, we can conclude:
θ=60∘
The angle at which the position-time graph of object B is inclined to the time axis is 60∘.
The correct answer is D. 60∘.
Topper's Solved these Questions
- MOTION IN STRAIGHT LINEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN STRAIGHT LINEEXERCISE - Assignment (SECTION - B)
19 Videos
- MOTION IN STRAIGHT LINEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN STRAIGHT LINEEXERCISE - Assignment (SECTION - C)
7 Videos
- MOTION IN STRAIGHT LINEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN STRAIGHT LINEEXERCISE - Try Yourself
40 Videos
- MOTION IN A STRAIGHT LINEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - ASSIGNMENT (SECTION - D)
15 Videos
- MOVING CHARGE AND MAGNESIUMBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOVING CHARGE AND MAGNESIUMEXERCISE - SECTION D
16 Videos
Similar Questions
Draw the position-time graph of a stationary object.
View SolutionThe position-time graph of an object is given below. What is the velocity of the object?

View SolutionThe position-time graph of an object is given below. What is the velocity of the object?

View SolutionThe position-time graph of an object is a straight line parallel to time axis. This implies that the object is
View SolutionDraw the position-time graph of an object moving with positive accceleration.
View SolutionThe x-t graph of an object is a straight line inclined to time-axis. What does this statement indicate ?
View SolutionDraw the position-time graph of a moving object, moving with zero acceleration.
View SolutionIf position time graph of particle is sine curve as shown, what will be its velocity-time graph.

View SolutionThe position - time (x−t) graph of an object in uniform motion is shown below, the velocity of object is
View SolutionThe position-time (x-t) graph of an object in uniform motion is shown below. Calculate the velocity with which the object is moving.
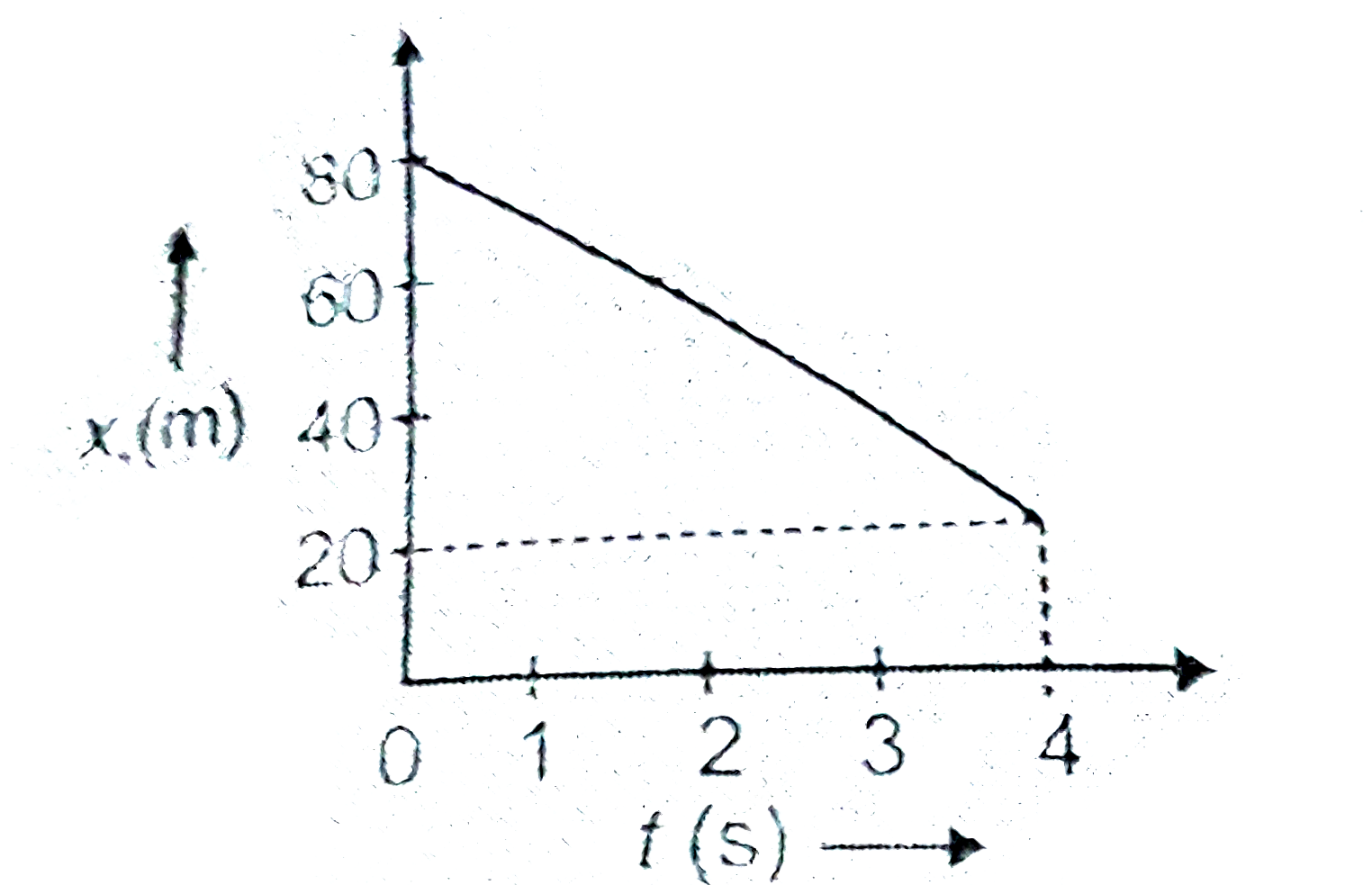
View Solution
