A bullet weighing 10 g and moving with a velocity 300 m/s strikes a 5 kg block of ice and drop dead. The ice block is kept on smooth surface. The speed of the block after the the collision is
6 cm/s
60 cm/s
6 m/s
0.6 cm/s
The correct Answer is:B
To solve the problem, we will use the principle of conservation of momentum. The momentum before the collision must equal the momentum after the collision.
1. Identify the given values:
- Mass of the bullet (m1) = 10 g = 10 × 10^(-3) kg = 0.01 kg
- Velocity of the bullet (u1) = 300 m/s
- Mass of the block of ice (m2) = 5 kg
- Initial velocity of the block of ice (u2) = 0 m/s (since it is at rest)
2. Write the conservation of momentum equation:
The total momentum before the collision is equal to the total momentum after the collision.
m1u1+m2u2=(m1+m2)v
where v is the final velocity of the block after the collision.
3. Substitute the known values into the equation:
(0.01kg)×(300m/s)+(5kg)×(0m/s)=(0.01kg+5kg)×v
Simplifying this gives:
3kg m/s=(5.01kg)×v
4. Solve for v:
v=3kg m/s5.01kg≈0.5984m/s
5. Convert v from m/s to cm/s:
Since 1m/s=100cm/s:
v≈0.5984m/s×100≈59.84cm/s
Rounding this gives approximately 60cm/s.
Final Answer:
The speed of the block after the collision is approximately 60 cm/s.
---
- Mass of the bullet (m1) = 10 g = 10 × 10^(-3) kg = 0.01 kg
- Velocity of the bullet (u1) = 300 m/s
- Mass of the block of ice (m2) = 5 kg
- Initial velocity of the block of ice (u2) = 0 m/s (since it is at rest)
The total momentum before the collision is equal to the total momentum after the collision.
m1u1+m2u2=(m1+m2)v
where v is the final velocity of the block after the collision.
(0.01kg)×(300m/s)+(5kg)×(0m/s)=(0.01kg+5kg)×v
Simplifying this gives:
3kg m/s=(5.01kg)×v
v=3kg m/s5.01kg≈0.5984m/s
Since 1m/s=100cm/s:
v≈0.5984m/s×100≈59.84cm/s
Rounding this gives approximately 60cm/s.
The speed of the block after the collision is approximately 60 cm/s.
Topper's Solved these Questions
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - Assignment (SECTION - B)
35 Videos
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - Assignment (SECTION - C)
80 Videos
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - EXERCISE
37 Videos
- WAVESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WAVESEXERCISE - ASSIGNMENT ( SECTION-D ( Assertion - Reason Type Questions ))
12 Videos
Similar Questions
A buttle weighting 10 g and moving with a velocity 800ms−1 strikes a 10 kg block resting on a frictionless surface. The speed of the block after the perfectly inelastic collision is approximately
View SolutionA bullet of mass m moving with velocity υ1 strikes a suspended wooden block of mass M as shown in the figure and sticks to it. If the block rises to a height y. the initial of the bullet is

View Solution
Knowledge Check
A bullet of mass m moving horizontally with a velocity v strikes a block of wood of mass M and gets embedded in the block. The block is suspended from the ceiling by a massless string. The height to which block rises is
Av22g(mM+m)2Bv22g(M+mm)2Cv22g(mM)2Dv22g(Mm)2
A bullet of mass m moving with velocity v strikes a block of mass M at rest and gets embedded into it. The kinetic energy of the composite block will be
View SolutionA steel ball of mass 0.5kg is fastened to a cord 20cm long and fixed at the far end and is released when the cord is horizontal. At the bottom of its path the ball strikes a 2.5kg steel block initially at rest on a frictionless surface. The collision is elastic. The speed of the block just after the collision will be.
View SolutionA bullet of mass 'm' moving with velocity 'u' passes through a wooden block of mass M=nm as shown in figure. The block is resting on a smooth horizontal floor. After passing through the block, velocity relative to the block is
 .
.
View SolutionA bullet of mass 0.04 kg moving with a speed of 600 m/s penetrates a heavy wooden block. It stops after a penetration of 500 cm. The resistive force exerted by the block on the bullet is
View SolutionA bullet of mass 0.01 kg and travelling at a speed of 500 m/s strikes a block of mass 2 kg which is suspended by a string of length 5m. The center of gravity of the block is found to rise a vertical distance of 0.1m, figure. What is the speed of the bullet after it emerges from the block ? (g=9.8m/s2).
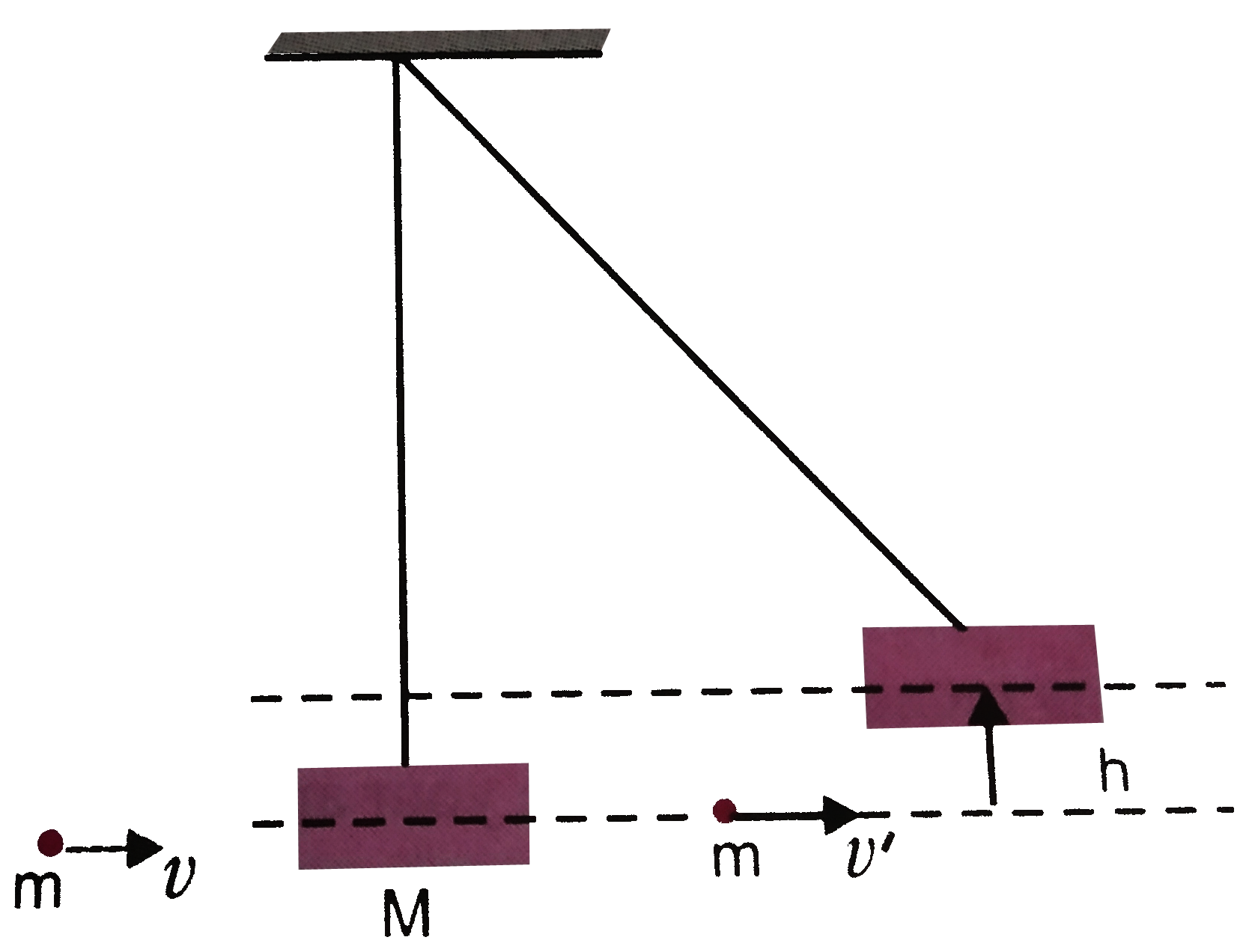
View SolutionA bullet of mass m moving with velocity υ1 strikes a suspended wooden block of mass M as shown in the figure and sticks to it. If the block rises to a height y. the initial of the bullet is

View SolutionA block of mass m moving at a velocity υ collides head on with another block of mass 2m at rest. If the coefficient of restitution is 1/2, find the velocities of the blocks after the collision.
View Solution
