A theif is running with speed of 10m/s along the line y=10m. The x−y plane is horizontal. A searchlight kept at the origin is always aimed at the theif. To do so its has to be continuosly rotated with some angular speed om≥a. When the line joining the thief with origin is making an angle θ=45∘ with the y axis, the value of ω is
1rad/s
2rad/s
14rad/s
12rad/s
To solve the problem, we need to determine the angular speed ω of the searchlight when the line joining the thief to the origin makes an angle of θ=45∘ with the y-axis.
1. Identify the position of the thief:
The thief is running along the line y=10m with a speed of 10m/s. Since he is moving horizontally, we can denote his position in Cartesian coordinates as (x,10).
2. Determine the angle:
When the line joining the thief to the origin makes an angle of 45∘ with the y-axis, it means that the angle with the x-axis is also 45∘. Thus, the coordinates of the thief can be expressed in terms of x as (x,10).
3. Calculate the distance R:
The distance R from the origin to the thief can be calculated using the Pythagorean theorem:
R=√x2+102
4. Determine the components of the velocity:
The thief's velocity V is 10m/s. We need to resolve this velocity into components:
- The component of velocity perpendicular to the line joining the thief and the origin is given by V⊥=Vsin(θ).
- Since θ=45∘, we have:
V⊥=10sin(45∘)=10⋅1√2=5√2m/s
5. Calculate the distance R when θ=45∘:
At θ=45∘, the coordinates of the thief can be expressed as:
x=10(since the thief is moving along y = 10)
Therefore, the distance R becomes:
R=√102+102=√200=10√2m
6. Calculate the angular speed ω:
The angular speed ω is given by the formula:
ω=V⊥R
Substituting the values we have:
ω=5√210√2=510=12rad/s
Final Answer:
The value of ω is 12rad/s.
---
The thief is running along the line y=10m with a speed of 10m/s. Since he is moving horizontally, we can denote his position in Cartesian coordinates as (x,10).
When the line joining the thief to the origin makes an angle of 45∘ with the y-axis, it means that the angle with the x-axis is also 45∘. Thus, the coordinates of the thief can be expressed in terms of x as (x,10).
The distance R from the origin to the thief can be calculated using the Pythagorean theorem:
R=√x2+102
The thief's velocity V is 10m/s. We need to resolve this velocity into components:
- The component of velocity perpendicular to the line joining the thief and the origin is given by V⊥=Vsin(θ).
- Since θ=45∘, we have:
V⊥=10sin(45∘)=10⋅1√2=5√2m/s
At θ=45∘, the coordinates of the thief can be expressed as:
x=10(since the thief is moving along y = 10)
Therefore, the distance R becomes:
R=√102+102=√200=10√2m
The angular speed ω is given by the formula:
ω=V⊥R
Substituting the values we have:
ω=5√210√2=510=12rad/s
The value of ω is 12rad/s.
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Assignment (Section - C) Objective Type Questions (More than one option are correct)
29 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Assignment (Section - D) Linked Comprehension Type Questions
20 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Assignment (Section - A) Objective Type Questions (One option is correct)
62 Videos
- SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSEXERCISE - Assignment (Section-D (Assertion and reason))
5 Videos
- TEST 1BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - TEST 1EXERCISE - EXERCISE
21 Videos
Similar Questions
A particle of mass 5g is moving with a uniform speed of 3√2cm/s in the x−y plane along the line y=x+4. The magnitude of its angular momentum about the origin in gcm2/s is
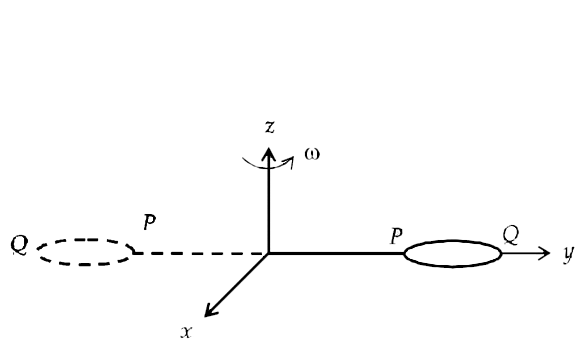
View SolutionThe general motion of a rigid body can be considered to be a combination of (i) a motion …. of its centre of mass about an axis, and (ii) its motion about an instantaneous axis passing through the centre of mass. These axes need not be stationary. Consider, for example, a thin uniform disc welded (rigidly fixed) horizontally at its rim to a massless stick, as shown in the figure. When the disc-stick system is rotated about the origin on a horizontal frictionless plane with angular speed ω , the motion at any instant can be taken as a combination of (i) a rotation of the centre of mass of the disc about the z-axis, and (ii) a rotation of the disc through an instantaneous vertical axis passing through its centre of mass (as is seen from the changed orientation of points P and Q). Both these motions have the same angular speed ω in this case.

Now consider two similar systems as shown in the figure: case (a) the disc with its face vertical and parallel to x-z plane, case (b) the disc with its face making an angle of 45° with x-y plane and its horizontal diameter parallel to x-axis. In both the cases, the disc is welded at point P, and the system are rotated with constant angular speed ω about the z-axis
Which of the following statement regarding the angular speed about the instantaneous axis (passing through the centre of mass) is correct ?
View SolutionA particle is moving with constant speed v along the line y = a in positive x -direction. Find magnitude of its angular velocity about orgine when its position makes an angle θ with x-axis.
View SolutionA particle is moving with constant speed v along the line y = a in positive x -direction. Find magnitude of its angular velocity about orgine when its position makes an angle θ with x-axis.
View SolutionA particle moves along the parabola y=x2 in the first quadrant in such a way that its x-coordinate (measured in metres) increases at a rate of 10 m/sec. If the angle of inclination θ of the line joining the particle to the origin change, when x = 3 m, at the rate of k rad/sec., then the value of k is
View SolutionA light rigid rod of length l is constrained to move in a vertical plane, so that its ends are along the x and y axes respectively. Find the instantaneous axis of rotation of the rod when it makes an angle θ with horizontal.

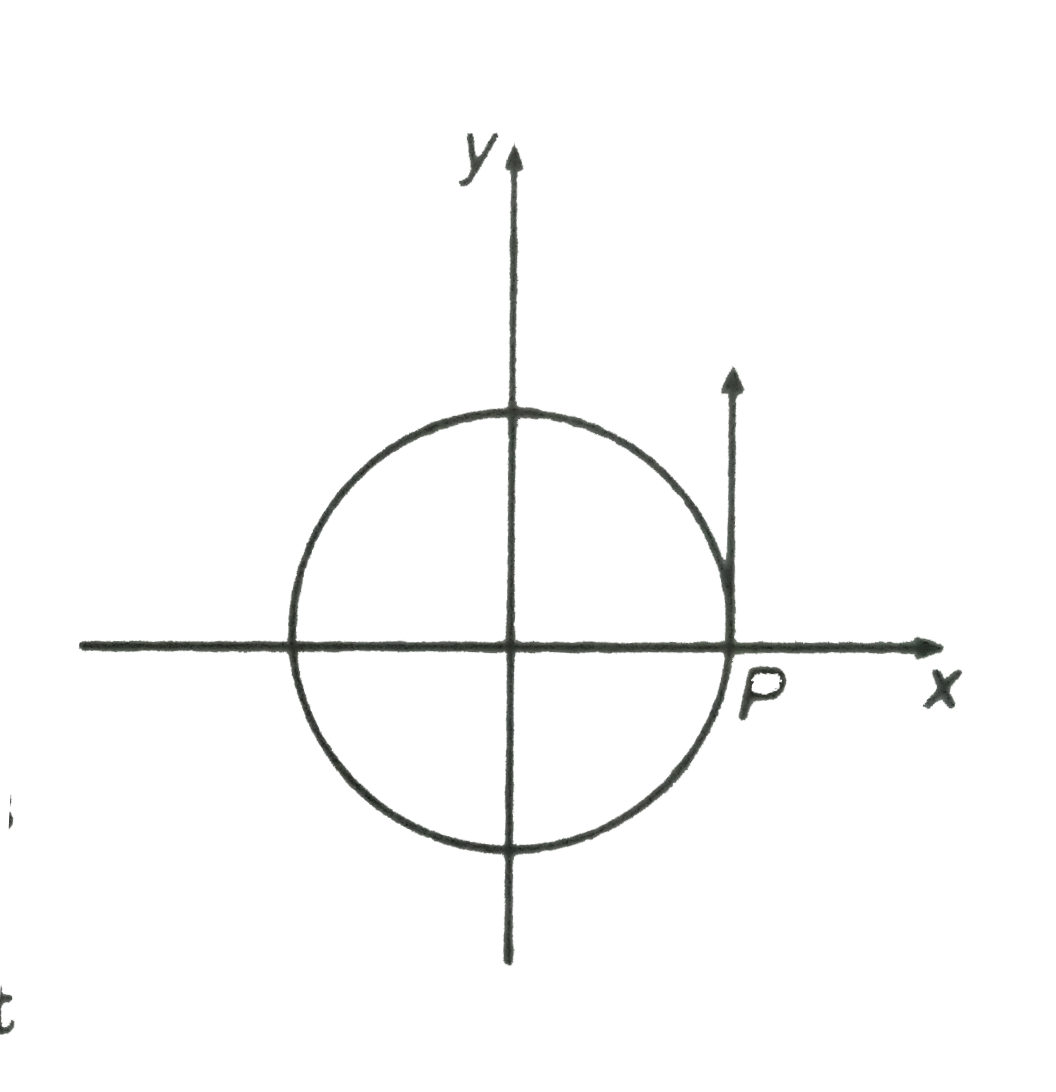
View SolutionA train is moving with a constant speed of 10m/s in a circle of radius 16πm. The plane of the circle lies in horizontal x-y plane. At time t = 0, train is at point P and moving in counter- clockwise direction. At this instant, a stone is thrown from the train with speed 10m/s relative to train towards negative x-axis at an angle of 37∘ with vertical z-axis . Find
(a) the velocity of particle relative to train at the highest point of its
trajectory.
(b) the co-ordinates of points on the ground where it finally falls and that of the hightest point of its trajectory. (Take g =10m/s2,sin37∘=35
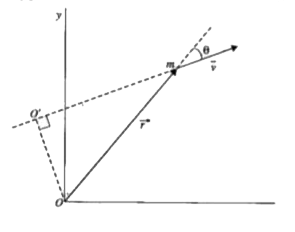
View SolutionA point mass 10 g moves in the xy plane with a velocity 2ms−1 along a straight line. Find the magnitude and direction of its angular momentum (i) with respect to the origin O and (ii) with respect to the origin O. The magnitude of the position vector →r is 0.5 m and the angle θ=30∘.
View SolutionThe general motion of a rigid body can be considered to be a combination of (i) a motion of its centre of mass about an axis, and (ii) its motion about an instantaneous exis passing through the centre of mass. These axes need not be stationary. Consider, for example, a thin uniform disc welded (rigidly fixed) horizontally at its rim to a massless, stick as shown in the figure. When the disc-stick system is rotated about the origin on a horizontal frictionless plane with angular speed ω the motion at any instant can be taken as a combination of (i) a rotation of the disc through an instantaneous vertical axis passing through its centre of mass (as is seen from the changed orientation of points P and Q). Both these motions have the same angular speed ω in this case
Now consider two similar system as shown in the figure: Case (a) the disc with its face vertical and parallel to x-z plane, Case (b) the disc with its face making an angle of 45∘ with x-y plane and its horizontal diameter parallel to x-axis. In both the cases, the disc is welded at point P, and the systems are rotated with constant angular speed ω about the z-axis.
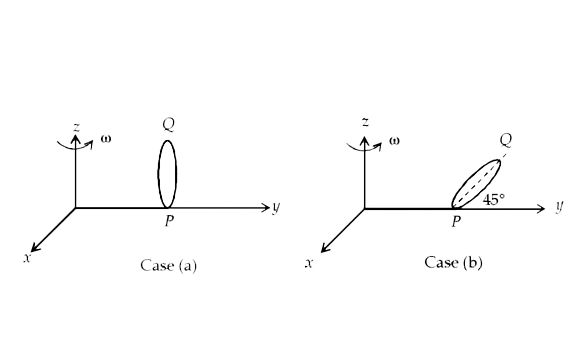
Which of the following statements regarding the angular speed about the instantaneous axis (passing through the centre of mass) is correct?
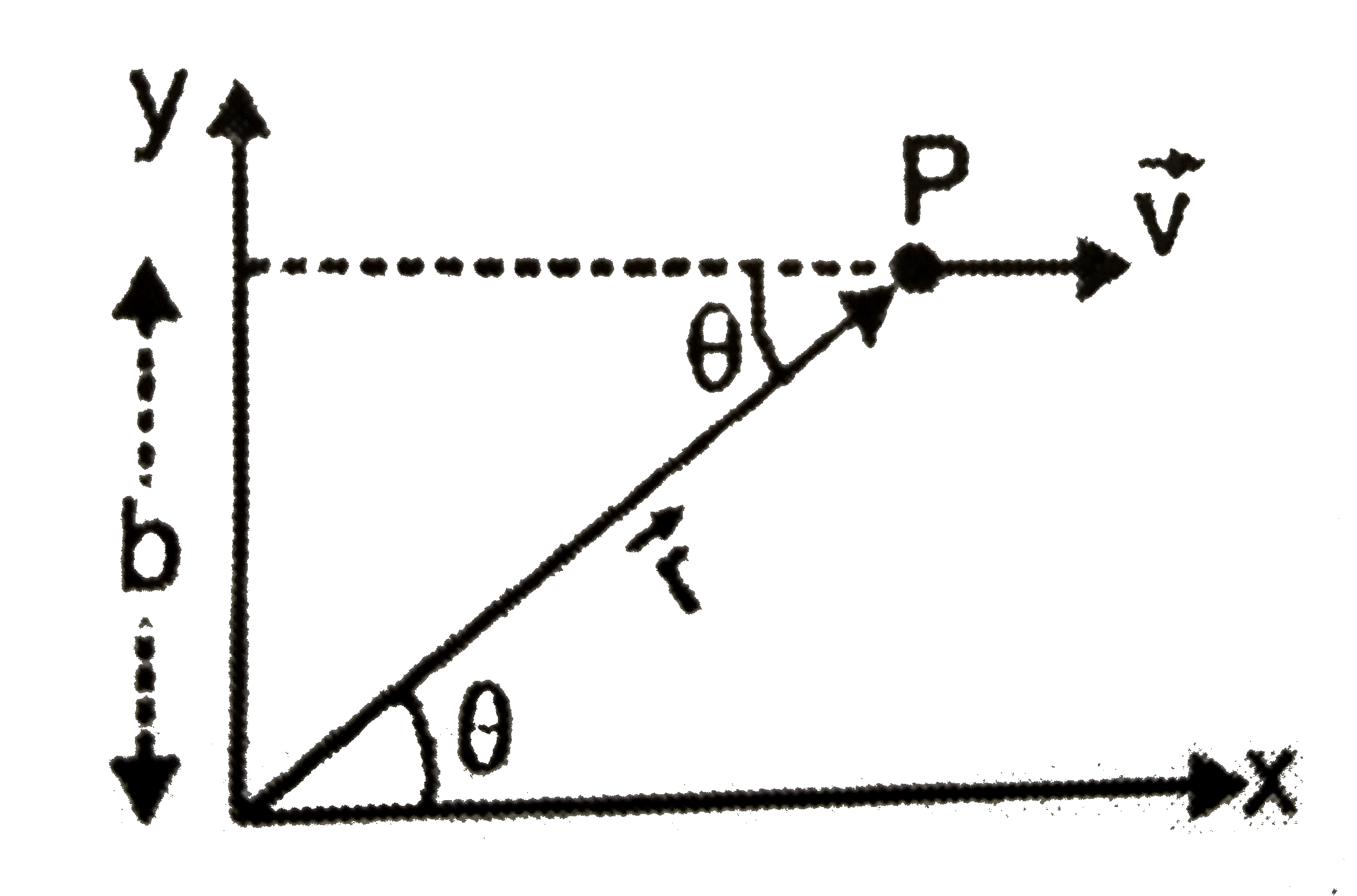
View SolutionA particle moving parallel to x-axis as shown in fig. such that at all instant the y-axis component of its position vector is constant and is equal to 'b'. Find the angular velocity of the particle about the origin when its radius vector makes angle θ from the axis.
View Solution
