An incompressible liquid of density is enclosed with two frictionless pistons one of cross-sectional area A and the other of 4 A. When the narrow piston moves out by a distance.
h
4 h
The correct Answer is:C
To solve the problem, we need to analyze the movement of the two pistons and the relationship between the volumes displaced by each piston.
1. Understanding the System:
- We have an incompressible liquid with density ρ enclosed between two frictionless pistons.
- The first piston has a cross-sectional area A and the second piston has a cross-sectional area 4A.
2. Displacement of the Narrow Piston:
- Let the narrow piston (area A) move out by a distance y.
- The volume displaced by this piston can be calculated as:
V1=A⋅y
3. Displacement of the Larger Piston:
- The larger piston (area 4A) will experience a change in volume due to the incompressibility of the liquid.
- If the larger piston moves in by a distance h, the volume displaced by this piston is:
V2=4A⋅h
4. Volume Conservation:
- Since the liquid is incompressible, the total volume of the liquid must remain constant. Therefore, the volume displaced by the narrow piston must equal the volume displaced by the larger piston:
V1=V2
- Substituting the expressions for V1 and V2:
A⋅y=4A⋅h
5. Simplifying the Equation:
- We can cancel A from both sides (since A≠0):
y=4h
6. Finding the Relationship:
- Rearranging the equation gives us:
h=y4
- This indicates that for every unit distance y that the narrow piston moves out, the larger piston moves in by a distance of y4.
Final Result:
Thus, the distance h that the larger piston moves in is:
h=y4
- We have an incompressible liquid with density ρ enclosed between two frictionless pistons.
- The first piston has a cross-sectional area A and the second piston has a cross-sectional area 4A.
- Let the narrow piston (area A) move out by a distance y.
- The volume displaced by this piston can be calculated as:
V1=A⋅y
- The larger piston (area 4A) will experience a change in volume due to the incompressibility of the liquid.
- If the larger piston moves in by a distance h, the volume displaced by this piston is:
V2=4A⋅h
- Since the liquid is incompressible, the total volume of the liquid must remain constant. Therefore, the volume displaced by the narrow piston must equal the volume displaced by the larger piston:
V1=V2
- Substituting the expressions for V1 and V2:
A⋅y=4A⋅h
- We can cancel A from both sides (since A≠0):
y=4h
- Rearranging the equation gives us:
h=y4
- This indicates that for every unit distance y that the narrow piston moves out, the larger piston moves in by a distance of y4.
Thus, the distance h that the larger piston moves in is:
h=y4
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF FLUIDSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - SECTION - B
23 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - SECTION - C
15 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - TRY YOURSELF
41 Videos
- MAGNETISM AND MATTER BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - ASSIGNMENT (SECTION D)
26 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - Assignment(Section-D)
14 Videos
Similar Questions
In the adjacent figure a cylindrical vessel of mass M and cross - sectional area A is placed inverted on a fixed smooth piston of same cross - sectional area fixed to the ground . The space between the cylinder and priston is completely filled with liquid of density ρ . There is a small office of cross - sectional area a (a<<A) at the top top portion of this vessel . ( intially length of the liquid column in the vessel is H )
Speed of the liquid with which it comes out of the vessel is

View SolutionIn the adjacent figure a cylindrical vessel of mass M and cross - sectional area A is placed inverted on a fixed smooth piston of same cross - sectional area fixed to the ground . The space between the cylinder and priston is completely filled with liquid of density ρ . There is a small office of cross - sectional area a (a<<A) at the top top portion of this vessel . ( intially length of the liquid column in the vessel is H ).Find the speed of the vessel with which it move
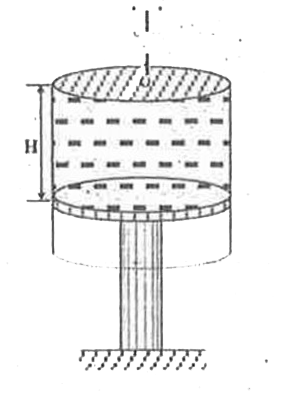
View SolutionA liquid of density ρ is filled in a vessel up to height H and a hole of cross section area A is made at a depth h below the free surface of liquid. The speed of liquid coming out of the hole is independent of
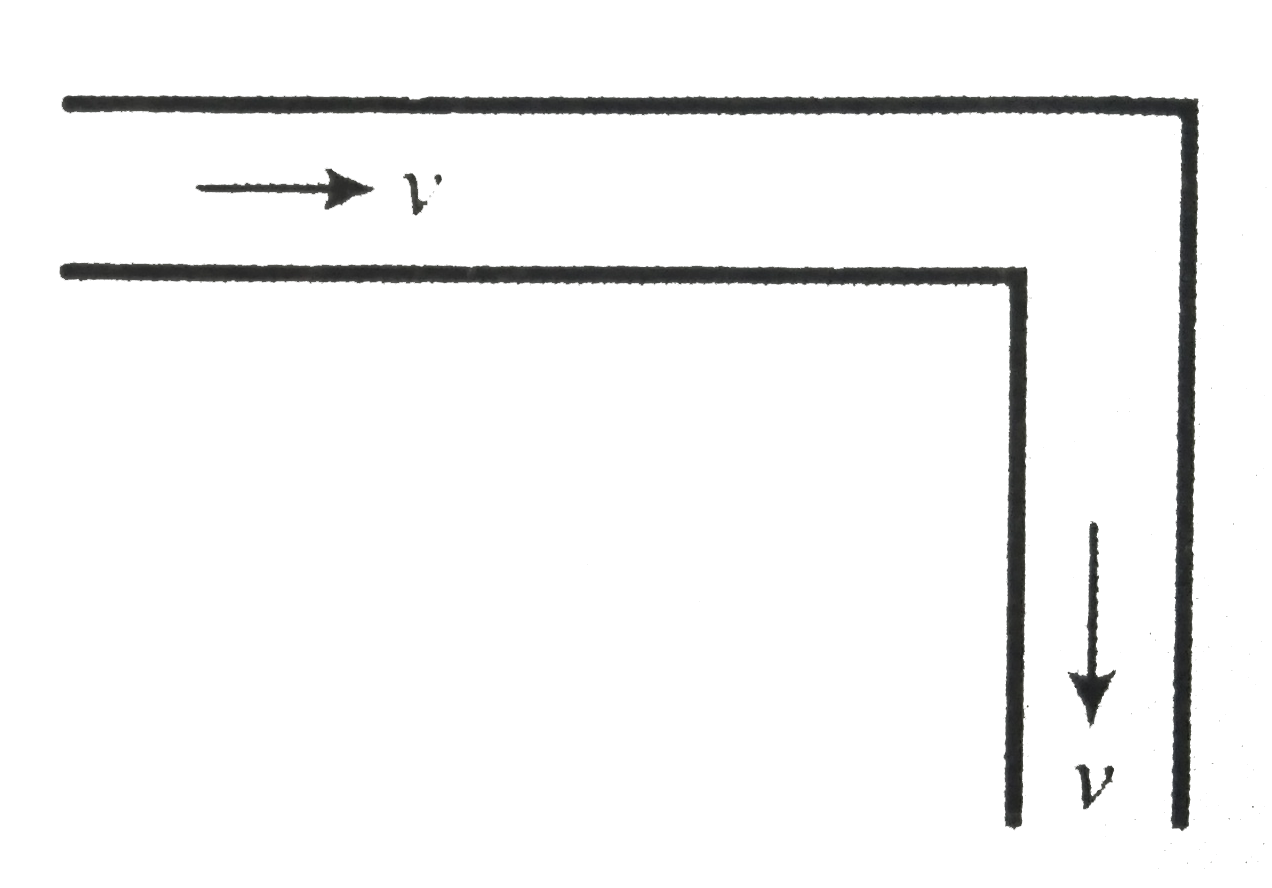
View SolutionA liquid of density ρ is flowing with a speed v through a pipe of cross sectional area A. The pipe is bent in the shape of a right angles as shown. What force should be exerted on the pipe at the corner to keep it fixed?
View SolutionA smooth vertical tube having two different cross sections is open from both the ends but closed by two sliding pistions as shown in Fig. and tied with an inextensible string. One mole of an ideal gas is enclosed between the piston The difference in cross-sectional areas of the two pistons is given ΔS. The masses of piston are m1 and m2 for larger and smaller one, respectively. Find the temperature by which tube is raised so that the pistons will be displaced by a distance l. Take atmospheric pressure equal to P0

View SolutionA smooth vertical tube having two different cross sections is open from both the ends but closed by two sliding pistions as shown in Fig. and tied with an inextensible string. One mole of an ideal gas is enclosed between the piston The difference in cross-sectional areas of the two pistons is given ΔS. The masses of piston are m1 and m2 for larger and smaller one, respectively. Find the temperature by which tube is raised so that the pistons will be displaced by a distance l. Take atmospheric pressure equal to P0

View SolutionA pump is used to pump a liquid of density ρ continuously through a pipe of cross, sectional area A. If liquid is flowing with speed v, then average power of pump is
View SolutionA pump is used to pump a liquid of density ρ continuously through a pipe of cross, sectional area A. If liquid is flowing with speed v, then average power of pump is
View SolutionA non viscous liquid of density ρ is filled in a tube with A as the area of cross section, as shown in the figure. If the liquid is slightly depressed in one of the arms, the liquid column oscillates with a frequency

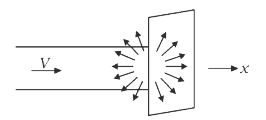
View SolutionA liquid of density ρ is flowing with a speed V through a pipe of cross sectional area A. What force does the liquid stream exert on wall in x direction if it splashes in the form of a circle after it hits the wall?
View Solution
