Maximum K.E. of a mass of 1 kg executing SHM is18 J . Amplitude of motion is6 cm , its angular frequency is
25rads−1
50rads−1
75rads−1
100rads−1
The correct Answer is:4
To solve the problem step by step, we will use the formula for the maximum kinetic energy (K.E.) in simple harmonic motion (SHM) and the given values.
Step 1: Write down the formula for maximum kinetic energy in SHM.
The maximum kinetic energy (K.E.) of an object executing SHM is given by the formula:
K.E.max=12mω2A2
where:
- K.E.max is the maximum kinetic energy,
- m is the mass of the object,
- ω is the angular frequency,
- A is the amplitude of the motion.
Step 2: Substitute the known values into the formula.
We know:
- K.E.max=18J
- m=1kg
- A=6cm=0.06m (convert cm to m)
Substituting these values into the formula:
18=12⋅1⋅ω2⋅(0.06)2
Step 3: Simplify the equation.
This simplifies to:
18=12⋅ω2⋅0.0036
18=0.0018⋅ω2
Step 4: Solve for ω2.
To isolate ω2, we can rearrange the equation:
ω2=180.0018
Calculating the right side:
ω2=10000
Step 5: Find ω.
Taking the square root of both sides gives us:
ω=√10000=100rad/s
Final Answer:
The angular frequency ω is 100rad/s.
---
The maximum kinetic energy (K.E.) of an object executing SHM is given by the formula:
K.E.max=12mω2A2
where:
- K.E.max is the maximum kinetic energy,
- m is the mass of the object,
- ω is the angular frequency,
- A is the amplitude of the motion.
We know:
- K.E.max=18J
- m=1kg
- A=6cm=0.06m (convert cm to m)
18=12⋅1⋅ω2⋅(0.06)2
This simplifies to:
18=12⋅ω2⋅0.0036
18=0.0018⋅ω2
To isolate ω2, we can rearrange the equation:
ω2=180.0018
Calculating the right side:
ω2=10000
Taking the square root of both sides gives us:
ω=√10000=100rad/s
The angular frequency ω is 100rad/s.
Topper's Solved these Questions
- OSCILLATIONSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - OSCILLATIONSEXERCISE - ASSIGNMENT (SECTION-B )
25 Videos
- OSCILLATIONSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - OSCILLATIONSEXERCISE - ASSIGNMENT ( SECTION-C )
11 Videos
- OSCILLATIONSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - OSCILLATIONSEXERCISE - Try Yourself
86 Videos
- NUCLEIBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - NUCLEIEXERCISE - ASSIGNMENT (SECTION-D)
10 Videos
- PHYSICAL WORLDBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - PHYSICAL WORLDEXERCISE - ASSIGNMENT (Section-B)
4 Videos
Similar Questions
A particle of mass 2 kg executing SHM has amplitude 10 cm and time period is 1 s.Find (i) the angular frequency (ii) the maximum speed (ii) the maximum acceleration (iv) the maximum restoring force (v) the speed when the displacement from the mean position is 8 cm (vi) the speed after 112 s the particle was at the extreme position (vii) the time taken by the particle to go directly from its mean position to half the amplitude (viii) the time taken by the particle to go directly from its exterme position to half the amplitude.
View SolutionA particle of mass 2kg executing SHM has amplitude 20cm and time period 1s. Its maximum speed is
View Solution
Knowledge Check
A particle of mass m executing SHM with amplitude A and angular frequency ω. The average value of the kinetic energy and potential energy over a period is
A0,12mω2A2B12mω2A2,0C12mω2A2,12mω2A2D14mω2A2,14mω2A2
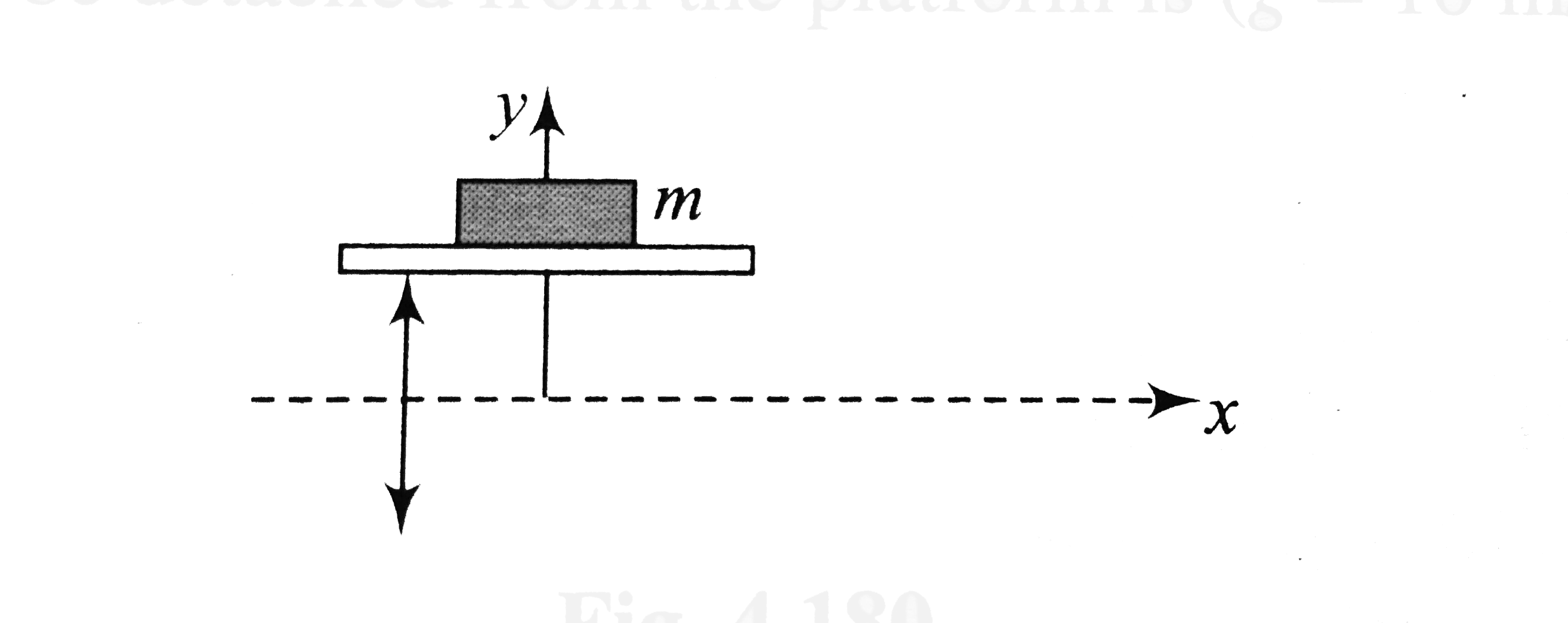
A horizontal platform with a mass m placed on it is executing SHM slong y-axis. If the amplitude of oscillation is 2.5 cm, the minimum period of the motion for the mass not to be detached from the platform (g=10ms2)
View Solution
A horizontal platform with a mass m placed on it is executing SHM slong y-axis. If the amplitude of oscillation is 2.5 cm, the minimum period of the motion for the mass not to be detached from the platform (g=10ms2)
View SolutionA particle of mass 2kg executing SHM has amplitude 20cm and time period 1s. Its maximum speed is
View SolutionA particle of mass 0.10 kg executes SHM with an amplitude 0.05 m and frequency 20 vib/s. Its energy of oscillation is
View SolutionAmplitude of a particle executing SHM is a and its time period is T. Its maximum speed is
View SolutionThe KE and PE , at is a particle executing SHM with amplitude A will be equal when its displacement is
View SolutionThe KE and PE , at is a particle executing SHM with amplitude A will be equal when its displacement is
View Solution
