Question

Which of the followings represent the variation of frequency (f) with radius of cross section of a stretched string?

Options

A.
B.
C.
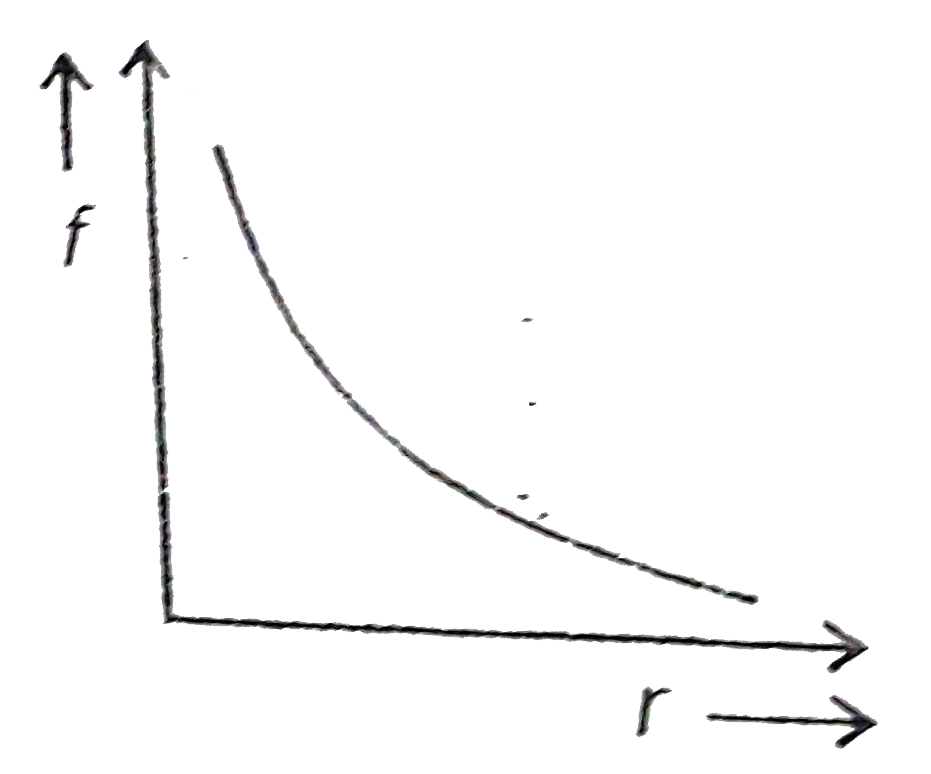
D. none of these

Answer

A

Explanation

To solve the problem of how frequency (f) varies with the radius (r) of the cross-section of a stretched string, we can follow these steps:

Step 1: Understand the formula for frequency of a stretched string
The frequency (f) of a stretched string can be expressed using the formula:
\( f = \frac{1}{2L} \sqrt{\frac{T}{\mu}} \)
where:
- \( T \) is the tension in the string,
- \( \mu \) is the mass per unit length,
- \( L \) is the length of the string.

Step 2: Relate mass per unit length to the radius
The mass per unit length (\( \mu \)) can be expressed in terms of the density (\( \rho \)) and the cross-sectional area (A) of the string:
\( \mu = \frac{m}{L} = \frac{\rho \cdot A}{L} \)
For a circular cross-section, the area (A) can be expressed as:
\( A = \pi r^2 \)
Thus, we can write:
\( \mu = \frac{\rho \cdot \pi r^2 \cdot L}{L} = \rho \cdot \pi r^2 \)

Step 3: Substitute \( \mu \) back into the frequency formula
Substituting \( \mu \) into the frequency formula gives:
\( f = \frac{1}{2L} \sqrt{\frac{T}{\rho \cdot \pi r^2}} \)

Step 4: Simplify the expression
This can be simplified to:
\( f = \frac{1}{2L} \cdot \sqrt{\frac{T}{\rho \cdot \pi}} \cdot \frac{1}{r} \)
Here, \( \frac{1}{2L} \cdot \sqrt{\frac{T}{\rho \cdot \pi}} \) is a constant (let's call it \( k \)):
\( f = \frac{k}{r} \)

Step 5: Conclude the relationship
From the equation \( f = \frac{k}{r} \), we can see that frequency (f) is inversely proportional to the radius (r) of the cross-section of the string.

Final Answer
Thus, the variation of frequency (f) with the radius (r) of the cross-section of a stretched string is represented by an inverse relationship, which can be depicted graphically as a hyperbola. Therefore, the correct option is Option A.

---