A long plank begins to move at t=0 and accelerates along a straight track wit a speed given by v=2t2 for 0≤t≤2 (where v is in m/s and t is in second). After 2 sec the plane continues to move at the constant speed acquired. A small initially at rest on the plank begins to slip at t=1 sec and stops sliding at t=3 sec. If the coefficient of static friction and kinetic friction between the plank and the block is 0.s and 0.k (where s and k are digits) respectively, find s+k (take g=10m/s2)
The correct Answer is:μs=0.4,μk=0.3
To solve the problem, we will follow these steps:
Step 1: Determine the velocity of the plank at t = 2 seconds
The velocity of the plank is given by the equation:
v=2t2
At t=2 seconds:
v=2(22)=2×4=8m/s
Step 2: Calculate the acceleration of the plank at t = 1 second
To find the acceleration, we differentiate the velocity with respect to time:
a=dvdt=d(2t2)dt=4t
At t=1 second:
a=4(1)=4m/s2
Step 3: Determine the static friction coefficient (μs)
At t=1 second, the block is about to slip. The force of static friction can be expressed as:
fs=μsN
Where N is the normal force, which equals mg (mass times gravitational acceleration). Therefore:
μsmg=ma
Cancelling mass m from both sides:
μsg=a
Substituting g=10m/s2 and a=4m/s2:
μs⋅10=4
μs=410=0.4
Step 4: Calculate the average acceleration from t = 1 to t = 3 seconds
At t=3 seconds, the velocity of the plank is still 8 m/s (constant speed after t = 2 seconds). The initial velocity at t=1 second can be calculated as:
v(1)=2(12)=2m/s
The average acceleration aavg from t=1 to t=3 seconds is:
aavg=vf−vitf−ti=8−23−1=62=3m/s2
Step 5: Determine the kinetic friction coefficient (μk)
Now we apply the same formula for kinetic friction:
fk=μkN
Where N=mg. Thus:
μkmg=maavg
Cancelling mass m:
μkg=aavg
Substituting g=10m/s2 and aavg=3m/s2:
μk⋅10=3
μk=310=0.3
Step 6: Find the sum of s and k
From our calculations:
- s=4 (from μs=0.4)
- k=3 (from μk=0.3)
Thus:
s+k=4+3=7
Final Answer
The value of s+k is 7.
---
The velocity of the plank is given by the equation:
v=2t2
At t=2 seconds:
v=2(22)=2×4=8m/s
To find the acceleration, we differentiate the velocity with respect to time:
a=dvdt=d(2t2)dt=4t
At t=1 second:
a=4(1)=4m/s2
At t=1 second, the block is about to slip. The force of static friction can be expressed as:
fs=μsN
Where N is the normal force, which equals mg (mass times gravitational acceleration). Therefore:
μsmg=ma
Cancelling mass m from both sides:
μsg=a
Substituting g=10m/s2 and a=4m/s2:
μs⋅10=4
μs=410=0.4
At t=3 seconds, the velocity of the plank is still 8 m/s (constant speed after t = 2 seconds). The initial velocity at t=1 second can be calculated as:
v(1)=2(12)=2m/s
The average acceleration aavg from t=1 to t=3 seconds is:
aavg=vf−vitf−ti=8−23−1=62=3m/s2
Now we apply the same formula for kinetic friction:
fk=μkN
Where N=mg. Thus:
μkmg=maavg
Cancelling mass m:
μkg=aavg
Substituting g=10m/s2 and aavg=3m/s2:
μk⋅10=3
μk=310=0.3
From our calculations:
- s=4 (from μs=0.4)
- k=3 (from μk=0.3)
s+k=4+3=7
The value of s+k is 7.
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Example
24 Videos
- LAWS OF MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - EXERCISE
69 Videos
- LAWS OF MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - ASSIGNMENT ( SECTION -I ) Subjective Type Questions
9 Videos
- KINETIC THEORYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - KINETIC THEORYEXERCISE - EXERCISE (ASSIGNMENT) SECTION - D Assertion - Reason Type Questions
10 Videos
- MAGNETISM AND MATTER BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - ASSIGNMENT (SECTION D)
26 Videos
Similar Questions
A car starts from rest at time t = 0 and it a-t graph is shown in figure. A coin is initially at rest on the floor of the car. At t = 1 s the coin begins to slip and it stops slipping at t = 3 s. The coefficient of static friction between the floor and the coin is (g = 10 m/s2)
_PHY_E05_188_Q02.png)
View SolutionThe speed(v) of a particle moving along a straight line is given by v=(t2+3t−4 where v is in m/s and t in seconds. Find time t at which the particle will momentarily come to rest.
View SolutionA car begains from rest at time t=0, and then acceleration along a straight track during the interval 0<t≤2s and thereafter with constant velocity as shown in figure in the graph. A coin is initially at rest on the floor of the car. At t=1s, the coin begains to slip and its stops slipping at t=3s . The coefficient of static friction between the floor and the coin is (g=10m/s2)
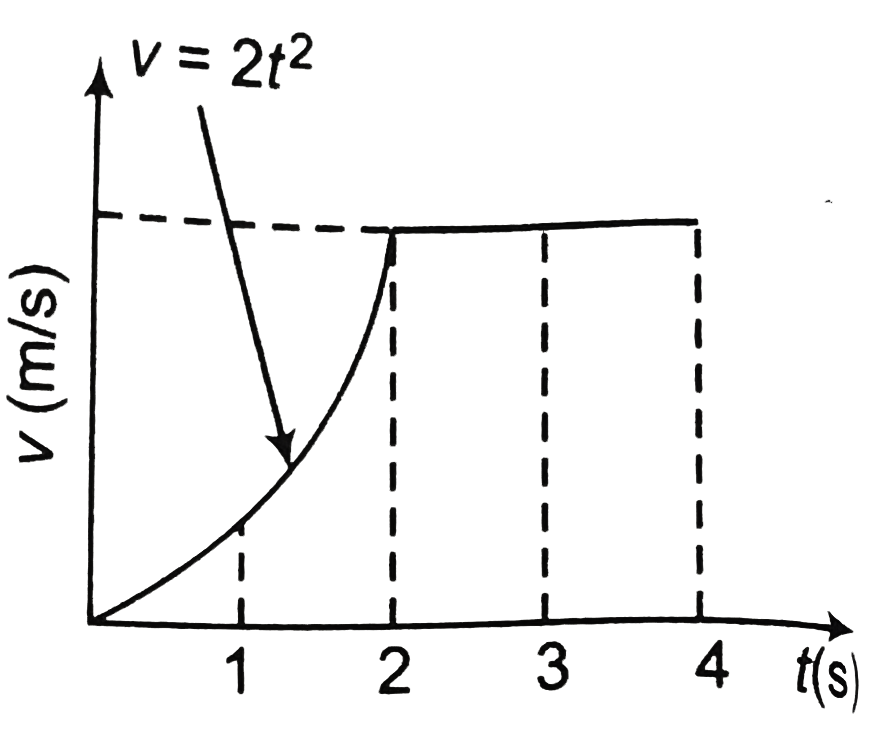
View SolutionThe velocity v of a body moving along a straight line varies with time t as v=2t2e−t, where v is in m/s and t is in second. The acceleration of body is zero at t =
View SolutionA car moves along a straight line whose equation of motion is given by
s=12t+3t2−2t3
where s is in metres and t is in seconds. The velocity of the car at start will be :-
View SolutionThe displacement of a point moving along a straight line is given by
s=4t2+5t−6
Here s is in cm and t is in seconds calculate
(i) Initial speed of particle
(ii) Speed at t=4s
View SolutionThe speed (v) and time (t) for an object moving along straight line are related as t2+100=2vt where v is in meter/second and t is in second. Find the possible positive values of v.
View SolutionThe speed (v) and time (t) for an object moving along straight line are related as t2+400=4vt where v is in meter/second and t is in second. Find the possible positive values of v.
View SolutionA particle moves in a circle of radius 2cm at a speed given by v=4t, where v is in cms−1 and t is in seconds.
(a) Find the tangential acceleration at t=1s
(b) Find total acceleration at t=1s.
View SolutionIf the particle is moving along a straight line given by the relation x=2−3t+4t3 where s is in cms., and t in sec. Its average velocity during the third sec is
View Solution
