Three point charges q,q/3 and 16q have to be arranged on positive x-axis within 20 cm, so that system's potential energy is minimum. Find the distance of charge q/3 from charge q.
The correct Answer is:4
To solve the problem of arranging the three point charges q, q3, and 16q on the positive x-axis such that the system's potential energy is minimized, we can follow these steps:
Step 1: Define the Arrangement
Let's place the charges on the x-axis:
- Charge q at position x1=0 cm.
- Charge q3 at position x2=x cm.
- Charge 16q at position x3=20 cm.
Step 2: Calculate the Potential Energy
The potential energy U of the system of charges can be expressed as the sum of the potential energies between each pair of charges:
U=U12+U23+U31
Where:
- U12=kq⋅q3x=kq23x
- U23=kq3⋅16q20−x=16kq23(20−x)
- U31=kq⋅16q20=16kq220
Thus, the total potential energy is:
U=kq23x+16kq23(20−x)+16kq220
Step 3: Simplify the Expression
We can factor out kq2:
U=kq2(13x+163(20−x)+1620)
Step 4: Differentiate the Potential Energy
To find the minimum potential energy, we need to differentiate U with respect to x and set the derivative to zero:
dUdx=−kq23x2+16kq23(20−x)2
Setting dUdx=0:
−13x2+163(20−x)2=0
Step 5: Solve for x
Cross-multiplying gives:
(20−x)2=16x2
Taking the square root:
20−x=4xor20−x=−4x
From 20−x=4x:
20=5x⇒x=4 cm
From 20−x=−4x:
20=−3x⇒x=−203 (not valid since distance cannot be negative)
Step 6: Verify Minimum
To ensure that this value of x gives a minimum potential energy, we can check the second derivative:
d2Udx2>0 at x=4
This confirms that x=4 cm is indeed the point where potential energy is minimized.
Final Answer
The distance of charge q3 from charge q is:
4 cm
Let's place the charges on the x-axis:
- Charge q at position x1=0 cm.
- Charge q3 at position x2=x cm.
- Charge 16q at position x3=20 cm.
The potential energy U of the system of charges can be expressed as the sum of the potential energies between each pair of charges:
- U12=kq⋅q3x=kq23x
- U23=kq3⋅16q20−x=16kq23(20−x)
- U31=kq⋅16q20=16kq220
We can factor out kq2:
To find the minimum potential energy, we need to differentiate U with respect to x and set the derivative to zero:
Cross-multiplying gives:
To ensure that this value of x gives a minimum potential energy, we can check the second derivative:
The distance of charge q3 from charge q is:
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCE Book:AAKASH INSTITUTE ENGLISHChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCE Exercise:SECTION-H Multiple True-False Type Questions
Explore 4 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE Book:AAKASH INSTITUTE ENGLISHChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCE Exercise:SECTION-I Subjective Type Questions
Explore 6 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE Book:AAKASH INSTITUTE ENGLISHChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCE Exercise:SECTION-F(MATRIX-MATCH TYPE QUESTIONS)
Explore 3 Videos
- ELECTROMAGNETIC WAVESBook:AAKASH INSTITUTE ENGLISHChapter:ELECTROMAGNETIC WAVESExercise:ASSIGNMENT SECTION - D Assertion-Reason Type Questions
Explore 25 Videos
- GRAVITATION Book:AAKASH INSTITUTE ENGLISHChapter:GRAVITATION Exercise:ASSIGNMENT SECTION - D (ASSERTION-REASON TYPE QUESTIONS)
Explore 15 Videos
Similar Questions
Two point charges Q and -Q/4 are separated by a distance x.

View SolutionThree point charge Q,4Q and 16Q are placed on a straight line 9cm long.Charges are placed in such a way that the system has minimum potential energy .Then
View SolutionThree charges -q,+2q, and -q are arranged on a line as shown in fig. Calculate the field at a distance r>>a on the line.
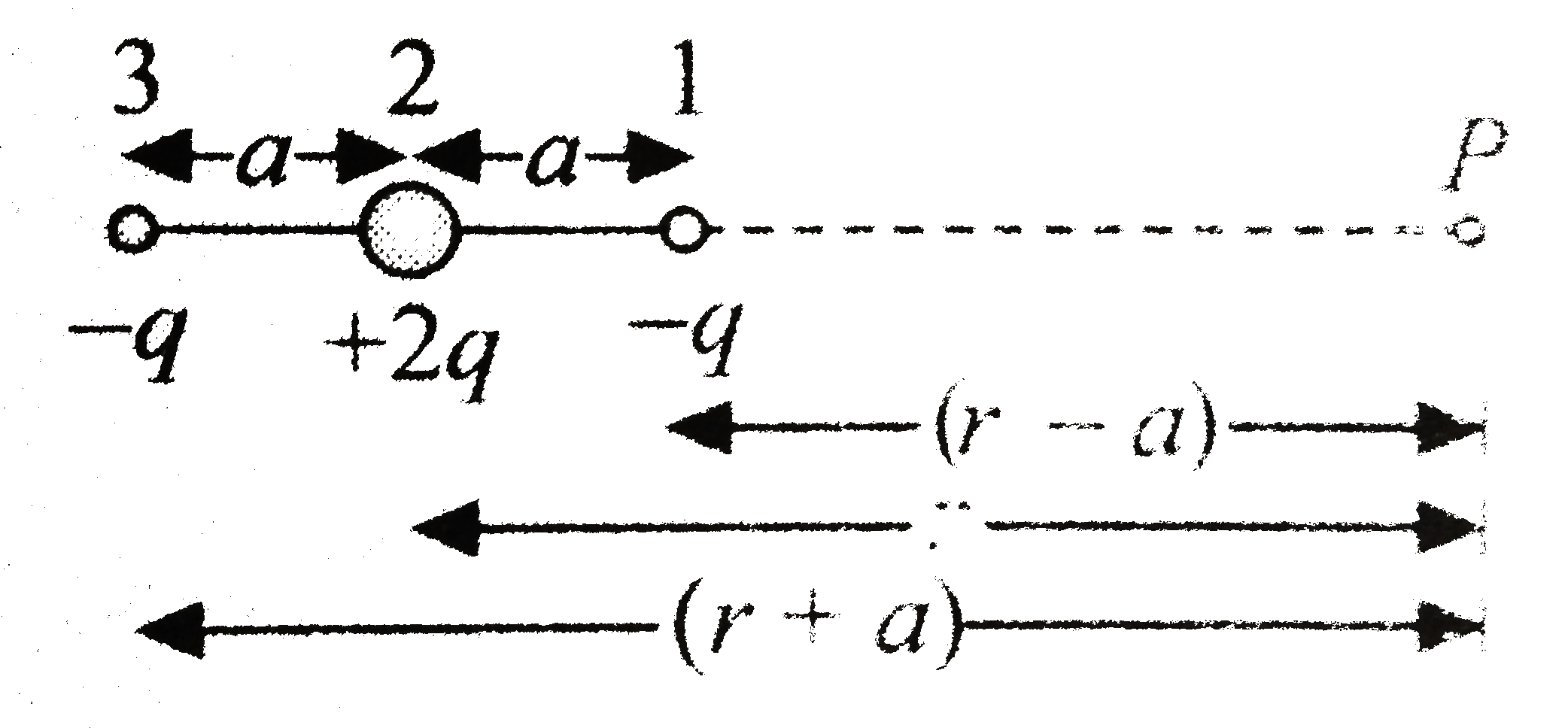
View SolutionThree point charges q, 2q and 8q are to be placed on a
. 9cm long straight line. Find the
. positions where the charges shouldbe placed such that the potential energy
. of this sysrem is minimum. In this situation, what is the
. electric field at the charge q due to the other two charges?
View Solution_2019_CBT3_E01_056_Q01.png)
three point charge −q,q and Q are arranged as given in figure. If d is distance from centre of −q and +q to Q and d>>>a then the potential energy of given system is
View SolutionTwo point charges +q and +4q are a distance l apart. A third charge q1 is so placed that the entire system is in equilibrium. Find the location, magnitude and sign of the third charge.
View SolutionSet up arrangment of three point charges : q,+2qandxq separated by equal finite distances so that electric potential energy of the system is zero. What is x ?
View SolutionThree charges −q,+Q and −q are placed in a straight line as shown

If the total potential energy of the system is zero, then the ratio qQ is
View SolutionCharges−q,Q,and−q are placed at an equal distance on a straight liner. If the total potential energy of the system of three charges is zero, then find the ratio Q/q.
 .
.
View SolutionTwo point charges +q and −q are placed a distance x apart. A third charge is so placed that at the three charges are in equilibrium. Then
View Solution
