There are three conducting and concentricspherical shells of radii R,2R and 3R. The charge on inner and outer most shells are q and 3q while middle shell is earthed. Find the ratio of number of field lines emitted by outermost shell and inner shell.
The correct Answer is:3
To solve the problem of finding the ratio of the number of electric field lines emitted by the outermost shell and the inner shell, we will follow a systematic approach:
Step 1: Understand the Configuration
We have three concentric spherical shells:
- Inner shell (Shell 1) with radius R and charge q.
- Middle shell (Shell 2) with radius 2R which is earthed (potential = 0).
- Outermost shell (Shell 3) with radius 3R and charge 3q.
Step 2: Determine the Charge on the Middle Shell
Since the middle shell is earthed, it will acquire a charge due to the influence of the inner and outer shells. We denote the charge on the middle shell as q′.
Using the principle of superposition and the fact that the potential of the middle shell must be zero, we can set up the equation for the potential at the middle shell due to the inner and outer shells:
V2=V1+V′+V3=0
Where:
- V1 is the potential due to the inner shell =kq2R
- V′ is the potential due to the middle shell itself =kq′2R
- V3 is the potential due to the outer shell =k(3q)3R
Setting the total potential to zero:
kq2R+kq′2R+k(3q)3R=0
Step 3: Solve for q′
Multiply through by 6R to eliminate the denominators:
3kq+3kq′+2k(3q)=0
This simplifies to:
3kq+3kq′+6kq=0
Combining like terms:
9kq+3kq′=0
Thus,
q′=−3q
Step 4: Calculate the Electric Field Lines
According to Gauss's law, the number of electric field lines (or electric flux) Φ is given by:
Φ=Qenclosedϵ0
For the Outermost Shell (Shell 3):
The charge enclosed by a Gaussian surface outside Shell 3 is:
Qenclosed=3q+(−3q)+q=q
Thus, the electric flux due to the outermost shell is:
Φ3=qϵ0
For the Inner Shell (Shell 1):
The charge enclosed by a Gaussian surface around Shell 1 is simply:
Qenclosed=q
Thus, the electric flux due to the inner shell is:
Φ1=qϵ0
Step 5: Find the Ratio of Electric Field Lines
Now, we can find the ratio of the electric field lines emitted by the outermost shell to those emitted by the inner shell:
Ratio=Φ3Φ1=qϵ0qϵ0=1
Final Answer
The ratio of the number of field lines emitted by the outermost shell to the inner shell is:
Ratio=3:1
We have three concentric spherical shells:
- Inner shell (Shell 1) with radius R and charge q.
- Middle shell (Shell 2) with radius 2R which is earthed (potential = 0).
- Outermost shell (Shell 3) with radius 3R and charge 3q.
Since the middle shell is earthed, it will acquire a charge due to the influence of the inner and outer shells. We denote the charge on the middle shell as q′.
V2=V1+V′+V3=0
Where:
- V1 is the potential due to the inner shell =kq2R
- V′ is the potential due to the middle shell itself =kq′2R
- V3 is the potential due to the outer shell =k(3q)3R
kq2R+kq′2R+k(3q)3R=0
Multiply through by 6R to eliminate the denominators:
3kq+3kq′+2k(3q)=0
This simplifies to:
3kq+3kq′+6kq=0
Combining like terms:
9kq+3kq′=0
Thus,
q′=−3q
According to Gauss's law, the number of electric field lines (or electric flux) Φ is given by:
Φ=Qenclosedϵ0
The charge enclosed by a Gaussian surface outside Shell 3 is:
Qenclosed=3q+(−3q)+q=q
Thus, the electric flux due to the outermost shell is:
Φ3=qϵ0
The charge enclosed by a Gaussian surface around Shell 1 is simply:
Qenclosed=q
Thus, the electric flux due to the inner shell is:
Φ1=qϵ0
Now, we can find the ratio of the electric field lines emitted by the outermost shell to those emitted by the inner shell:
Ratio=Φ3Φ1=qϵ0qϵ0=1
The ratio of the number of field lines emitted by the outermost shell to the inner shell is:
Ratio=3:1
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - SECTION-H Multiple True-False Type Questions
4 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - SECTION-I Subjective Type Questions
6 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - SECTION-F(MATRIX-MATCH TYPE QUESTIONS)
3 Videos
- ELECTROMAGNETIC WAVESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - ASSIGNMENT SECTION - D Assertion-Reason Type Questions
25 Videos
- GRAVITATION BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - GRAVITATION EXERCISE - ASSIGNMENT SECTION - D (ASSERTION-REASON TYPE QUESTIONS)
15 Videos
Similar Questions
There are two concentric conducting spherical shells of radii 10cm and 20cm. The outer shell is charged to a potential of 50esu while inner shell is earthed. The charge on outer shell is
View SolutionFigure shows three concentric metallic spherical shells. The outermost shell has charge q2, the inner most shell has charge q1, and the middle shell is uncharged. The charge appearing on the inner surface of outermost shell is
View SolutionTwo thin conducting shells of radii R and 3R are as shown in the fig. External shell carries a charge +Q and inner shell neutral. The inner shell is earthed with the help of a switch S. Then

View SolutionFigure shows two conducting thin concentric shells of radi r and 3r. The outer shell carries a charge q. Inner shell in neutral. Find the charge that wilL flow from inner shell to earth the switch S is closed.
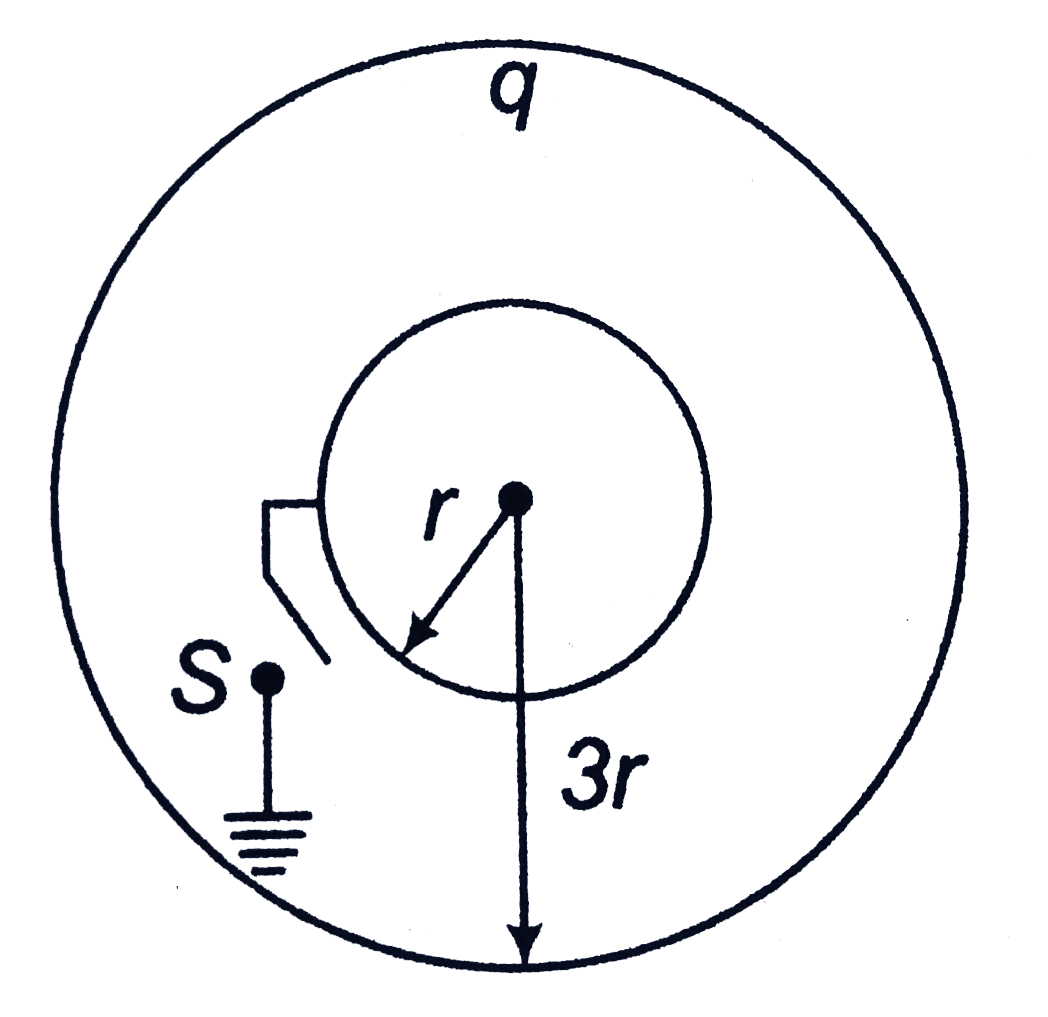
View SolutionFigure shows two conducting thin concentric shells of radi r and 3r. The outer shell carries a charge q. Inner shell in neutral. Find the charge that wilL flow from inner shell to earth the switch S is closed.

View SolutionThere are two concentric spherical shell of radii r and 2r. Initially, a charge Q is given to the inner shell and both the switches are open.

If switch S1 is closed and then opened, charge on the outer shell will be
View SolutionThere are two concentric hollow conducting spherical shells of radii r and R(R>r). The charge on the outer shell is Q. What charge should be given to the inner shell, so that the potential at a point P , at a distance 2R from the common centre is zero ?
View SolutionThree concentric conducting spherical shells of radii R, R2 and 3R carry charges Q,-2Q and 3Q, respectively compute the electric field at r=52R

View SolutionTwo concentric conducting shells of radii R and 2R are having charges Q and -2Q respectively.In a region r
View SolutionConsider two concentric metalic shell's of radii R and 2R. The inner shell is having charge Q and outer shell is uncharged. If they are connected with a conducting wire. Then,
View Solution