A battery delivers equal power individually across 4Ω and 16Ω . Internal resistance of the cell is
8Ω
6Ω
12Ω
20Ω
The correct Answer is:1
To solve the problem step by step, we need to find the internal resistance of the battery given that it delivers equal power across two resistors of 4 ohms and 16 ohms.
Step 1: Define the power equations for both resistors.
The power delivered across a resistor can be calculated using the formula:
P=I2R
where I is the current through the resistor and R is the resistance.
For the 4-ohm resistor:
P1=I21⋅4
For the 16-ohm resistor:
P2=I22⋅16
Step 2: Calculate the currents I1 and I2.
Using Ohm's law, the current through each resistor can be calculated as follows:
For the 4-ohm resistor:
I1=E4+r
For the 16-ohm resistor:
I2=E16+r
where E is the EMF of the battery and r is the internal resistance.
Step 3: Substitute the currents into the power equations.
Now we substitute I1 and I2 into the power equations:
For the 4-ohm resistor:
P1=(E4+r)2⋅4
For the 16-ohm resistor:
P2=(E16+r)2⋅16
Step 4: Set the powers equal to each other.
Since the problem states that the power delivered is equal for both resistors, we can set the two power equations equal to each other:
(E4+r)2⋅4=(E16+r)2⋅16
Step 5: Simplify the equation.
We can cancel E2 from both sides (assuming E≠0):
4(4+r)2=16(16+r)2
Cross-multiplying gives:
4(16+r)2=16(4+r)2
Step 6: Expand both sides.
Expanding both sides:
4(256+32r+r2)=16(16+8r+r2)
1024+128r+4r2=256+128r+16r2
Step 7: Rearrange the equation.
Rearranging gives:
1024−256=16r2−4r2
768=12r2
Step 8: Solve for r.
Dividing both sides by 12:
r2=76812=64
Taking the square root:
r=8Ω
Conclusion:
The internal resistance of the cell is r=8Ω.
---
The power delivered across a resistor can be calculated using the formula:
P=I2R
where I is the current through the resistor and R is the resistance.
P1=I21⋅4
P2=I22⋅16
Using Ohm's law, the current through each resistor can be calculated as follows:
I1=E4+r
I2=E16+r
Now we substitute I1 and I2 into the power equations:
P1=(E4+r)2⋅4
P2=(E16+r)2⋅16
Since the problem states that the power delivered is equal for both resistors, we can set the two power equations equal to each other:
(E4+r)2⋅4=(E16+r)2⋅16
We can cancel E2 from both sides (assuming E≠0):
4(4+r)2=16(16+r)2
4(16+r)2=16(4+r)2
Expanding both sides:
4(256+32r+r2)=16(16+8r+r2)
1024+128r+4r2=256+128r+16r2
Rearranging gives:
1024−256=16r2−4r2
768=12r2
Dividing both sides by 12:
r2=76812=64
Taking the square root:
r=8Ω
The internal resistance of the cell is r=8Ω.
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - ASSIGNMENT SECTION-B(OBJECTIVE TYPE QUESTION ))
44 Videos
- CURRENT ELECTRICITYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - ASSIGNMENT SECTION-C(OBJECTIVE TYPE QUESTION ))
13 Videos
- CURRENT ELECTRICITYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Try Yourself
34 Videos
- COMMUNICATION SYSTEMS BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - COMMUNICATION SYSTEMS EXERCISE - ASSIGNMENT SECTION D (Assertion-Reason)
10 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - ASSIGNMENT (SECTION-D)
10 Videos
Similar Questions
A battery of EMF E produces currents 4 A and 3 A when connected to external resistance 1Ω and 2Ω respectively. The internal resistance of the battery is
View SolutionA current of 2A flows through a 2Ω resistor when connected across a battery. The same battery supplies a current of 0.5A when connected across a 9Ω resistor. The internal resistance of the battery is
View SolutionA current of 2A flows through a 2Ω resistor when connected across a battery. The same battery supplies a current of 0.5A when connected across a 9Ω resistor. The internal resistance of the battery is
View SolutionIn a potentiometer experiment, the galvanometer shows no deflection when a cell is connected across 60cm of the potentiometer wire. If the cell is shunted by a resistance of 6Ω, the balance is obtained across 50cm of the wire. The internal resistance of the cell is
View SolutionA potentiometer circuit with potentiometer wire 10 m long, and an ideal main battery of e.m.f 8 V, has been set up for finding the internal resistance of a given cell. When the resistance R, connected across the given cell, has values of (i) infinity, (ii) 10 omega , the balancing lengths, on the potentiometer wire are found to be 2.4 m and x respectively. If the internal resistance of the cell is 2 ω, the value of x is
View SolutionIf all resistors in the shown network are of equal resistance, and the battery is of emf equal to 10 V and internal resistance equal to 1Ω, what should be resistance of each resistor so that the battery delivers maximum power
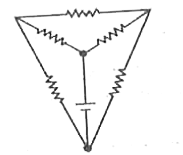
View SolutionWhen a battery connected across a resistor of 16Ω, the voltage across the resistor is 12 V. When the same battery is connected across a resistor of 10Ω, voltage across it is 11 V. The internal resistance of the battery (in ohm) is
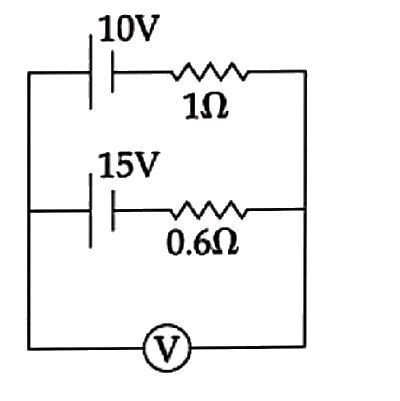
View SolutionA 10 V battery with internal resistance 1Ω and a 15 V battery with internal resistance 0.6Ω are connected in parallel to a voltmeter (see figure). The reading in the voltmeter will be close to:
View SolutionIn the circuit shown in figure, power developed across 1Ω,2Ω and 3Ω resistance are in the ratio of
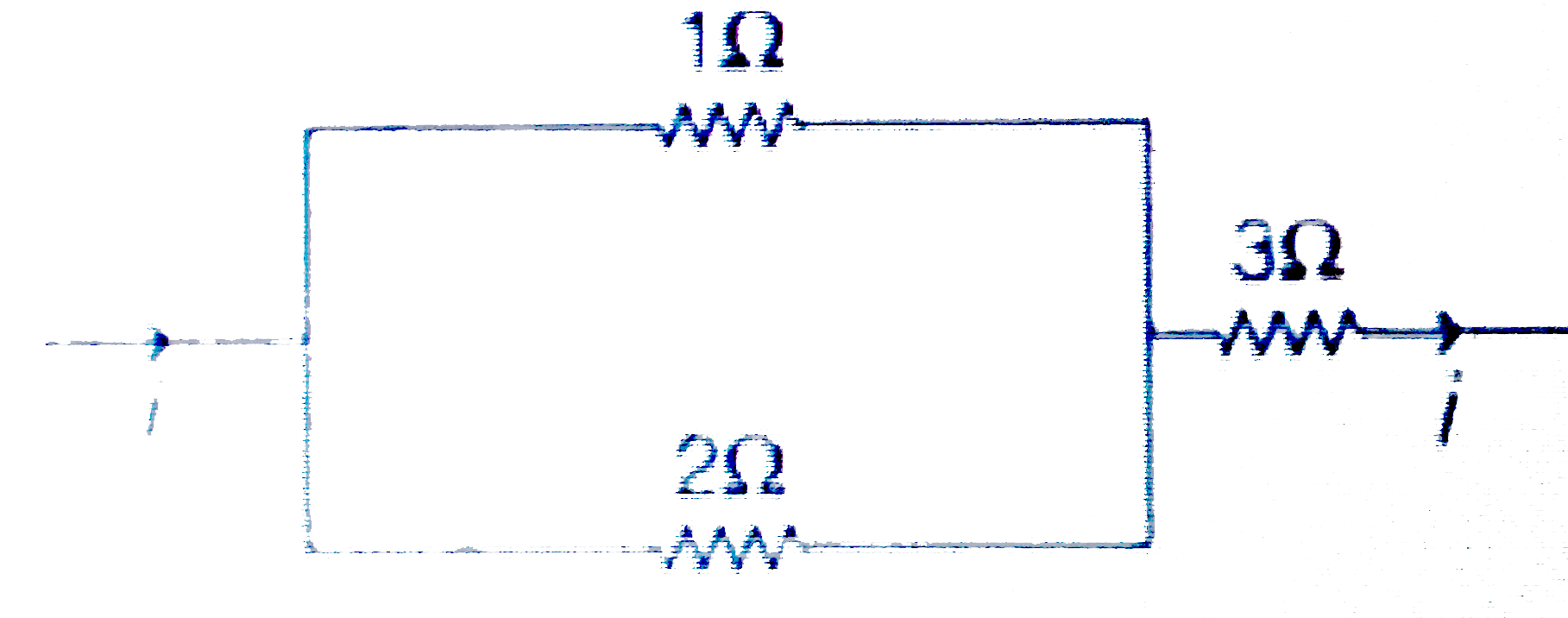
View SolutionA cell which has an emf 1.5 V is connectedin series with an external resistance of 10Ω. If the potential difference across the cell is 1.25 V, then the internal resistance of the cell is (inΩ)
View Solution
