A cell which has an emf 1.5 V is connectedin series with an external resistance of 10Ω. If the potential difference across the cell is 1.25 V, then the internal resistance of the cell is (inΩ)
2
0.25
1.5
0.3
The correct Answer is:A
To find the internal resistance of the cell, we can use the following steps:
Step 1: Identify the given values
- EMF of the cell (E) = 1.5 V
- Potential difference across the cell (V) = 1.25 V
- External resistance (R) = 10 Ω
Step 2: Use the formula for internal resistance
The internal resistance (r) of the cell can be calculated using the formula:
r=E−VI
Where:
- I is the current flowing through the circuit.
Step 3: Calculate the current (I)
Since the cell and the external resistance are in series, the current can be calculated using Ohm's law:
I=VR
However, we need to find the current using the EMF and the total resistance (which includes both the external resistance and the internal resistance).
The total voltage across the external resistance is given by:
V=I⋅R
Thus, we can rearrange this to find the current:
I=VR=1.2510=0.125A
Step 4: Substitute the values into the internal resistance formula
Now we can substitute the values into the internal resistance formula:
r=E−VI
Substituting the known values:
r=1.5−1.250.125
Step 5: Calculate the internal resistance
Now, calculate the numerator:
1.5−1.25=0.25
Then divide by the current:
r=0.250.125=2Ω
Final Answer
The internal resistance of the cell is 2Ω.
---
- EMF of the cell (E) = 1.5 V
- Potential difference across the cell (V) = 1.25 V
- External resistance (R) = 10 Ω
The internal resistance (r) of the cell can be calculated using the formula:
r=E−VI
Where:
- I is the current flowing through the circuit.
Since the cell and the external resistance are in series, the current can be calculated using Ohm's law:
I=VR
However, we need to find the current using the EMF and the total resistance (which includes both the external resistance and the internal resistance).
V=I⋅R
Thus, we can rearrange this to find the current:
I=VR=1.2510=0.125A
Now we can substitute the values into the internal resistance formula:
r=E−VI
Substituting the known values:
r=1.5−1.250.125
Now, calculate the numerator:
1.5−1.25=0.25
Then divide by the current:
r=0.250.125=2Ω
The internal resistance of the cell is 2Ω.
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - B. Assertion and reason
18 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Match the columns
4 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Check point
70 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Subjective
11 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Medical entrances gallery
25 Videos
Similar Questions
A cell has an emf 1.5V. When connected across an external resistance of 2Ω, the terminal potential difference falls to 1.0V. The internal resistance of the cell is:
View SolutionThe emf of a daniel cell is 1.08V. When the terminals of the cell are connected to resistance of 3Ω, the potential difference across the terminals is found to be 0.6 V. Then , the internal resistance of the cell is
View SolutionA cell of emf E is connected across a resistance R. The potential difference between the terminals of the cell is found to be V. The internal resistance of the cell must be -
View SolutionIf E is the emf of a cell of internal resistance r and external resistance R, then potential difference across R is given as
View SolutionTwo cells of the same e.mf. e but different internal resistances r1andr2 are connected in series with an external resistance 'R'. The potential drop across the first cell is found to be zero. The external resistance Ris

View Solution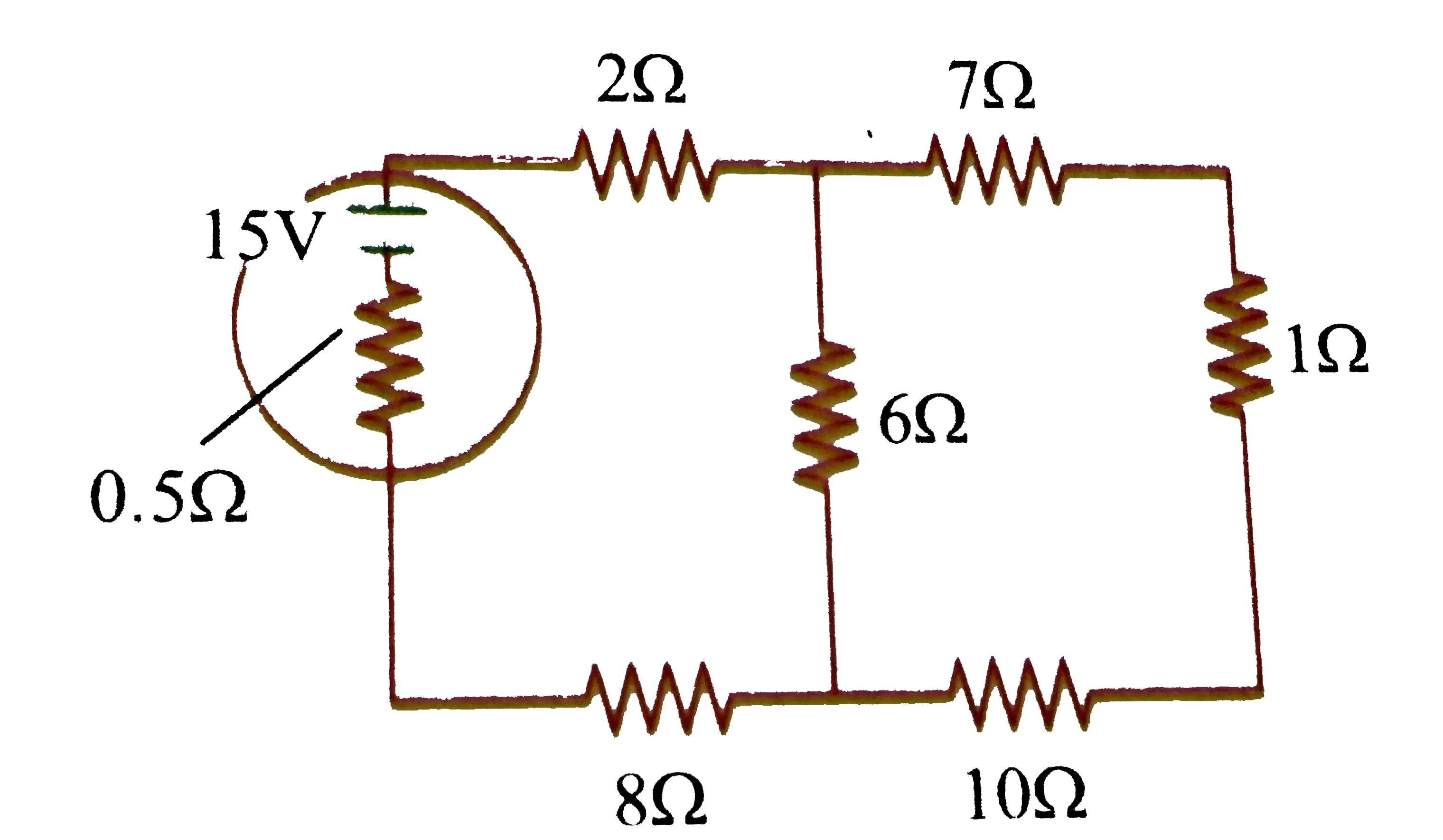
The emf of a cell E is 15 V as shown in the figure with an internal resistance of 0.5Ω. Then the value of the current drawn from the cell is
View SolutionThe n rows each containinig m cells in series are joined parallel. Maximum current is taken from this combination across jan external resistance of 3Ω resistance. If the total number of cells used are 24 and internal resistance of each cell is 0.5Ω then
View SolutionA voltmeter of resistance 994Ω is connected across a cell of emf 1 V and internal resistance 6Ω. Find the potential difference across the voltmeter, that across the terminals of the cell and percantage error in the reading of the voltmeter.
View SolutionAn ideal cell of emf 10 V is connected in circuit shown in figure. Each resistance is 2Ω . The potential difference (in V) across the capacitor when it is fully charged is _______.
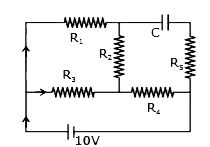
View SolutionA cell of e.m.f. 1.8 V and internal resistance 2 Ω is connected in series with an ammeter of resistance 0.7 Ω and a resistor of 4.5 Ω as shown in Fig. What is the potential difference across the terminals of the cell ?
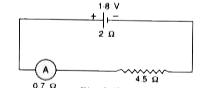
View Solution
