A potentiometer circuit with potentiometer wire 10 m long, and an ideal main battery of e.m.f 8 V, has been set up for finding the internal resistance of a given cell. When the resistance R, connected across the given cell, has values of (i) infinity, (ii) 10 omega , the balancing lengths, on the potentiometer wire are found to be 2.4 m and x respectively. If the internal resistance of the cell is 2 ω, the value of x is
1m
6m
2m
8m
To solve the problem, we will use the principles of a potentiometer and the relationship between the balancing lengths and the internal resistance of the cell. Here’s a step-by-step solution:
Step 1: Understand the Setup
We have a potentiometer circuit with a total length of 10 m and an ideal main battery of EMF 8 V. We are measuring the internal resistance of a given cell with known internal resistance r=2Ω.
Step 2: Identify the Given Values
- Balancing length when resistance R is infinite: l1=2.4m
- Balancing length when resistance R=10Ω: l2=x
- Internal resistance of the cell: r=2Ω
Step 3: Use the Potentiometer Formula
When the resistance R is infinite, the entire EMF of the cell is balanced by the potentiometer. The potential difference across the cell can be expressed as:
V=l1L⋅E
Where L is the total length of the potentiometer wire and E is the EMF of the cell.
When R=10Ω, the potential difference across the cell can be expressed as:
V′=l2L⋅E
Step 4: Set Up the Equations
From the first scenario (infinite resistance), we can write:
V=E⋅l1L=8⋅2.410
This gives us the voltage across the cell when R is infinite.
From the second scenario (with R=10Ω), we have:
V′=E⋅l2L=8⋅x10
Step 5: Relate the Two Scenarios Using Internal Resistance
The voltage across the cell can also be expressed in terms of the internal resistance and the external resistance:
V′=E⋅RR+r
Substituting R=10Ω and r=2Ω:
V′=8⋅1010+2=8012=203V
Step 6: Equate the Two Expressions for Voltage
Now we can equate the two expressions for V′:
8⋅x10=203
Step 7: Solve for x
Now, solve for x:
8x10=203
Cross-multiplying gives:
8x⋅3=20⋅10
24x=200
x=20024=253≈8.33m
Final Answer
The value of x is approximately 8.33m.
---
We have a potentiometer circuit with a total length of 10 m and an ideal main battery of EMF 8 V. We are measuring the internal resistance of a given cell with known internal resistance r=2Ω.
- Balancing length when resistance R is infinite: l1=2.4m
- Balancing length when resistance R=10Ω: l2=x
- Internal resistance of the cell: r=2Ω
When the resistance R is infinite, the entire EMF of the cell is balanced by the potentiometer. The potential difference across the cell can be expressed as:
V=l1L⋅E
Where L is the total length of the potentiometer wire and E is the EMF of the cell.
V′=l2L⋅E
From the first scenario (infinite resistance), we can write:
V=E⋅l1L=8⋅2.410
This gives us the voltage across the cell when R is infinite.
V′=E⋅l2L=8⋅x10
The voltage across the cell can also be expressed in terms of the internal resistance and the external resistance:
V′=E⋅RR+r
Substituting R=10Ω and r=2Ω:
V′=8⋅1010+2=8012=203V
Now we can equate the two expressions for V′:
8⋅x10=203
Now, solve for x:
8x10=203
Cross-multiplying gives:
8x⋅3=20⋅10
24x=200
x=20024=253≈8.33m
The value of x is approximately 8.33m.
Topper's Solved these Questions
- TEST 1BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - TEST 1EXERCISE - EXERCISE
21 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Try Yourself
63 Videos
- TEST 2BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - TEST 2EXERCISE - Exercise
308 Videos
Similar Questions
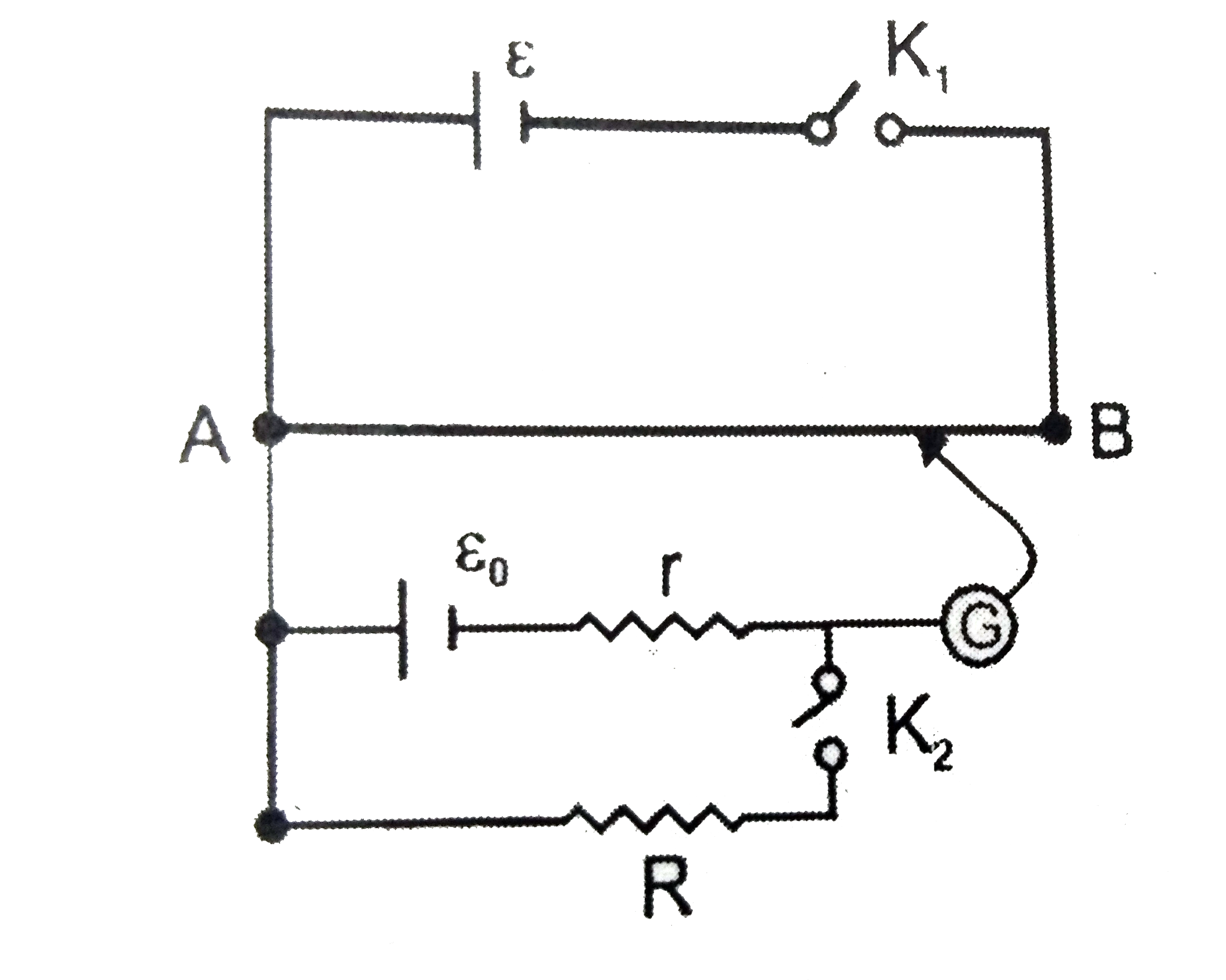
A potentiometer circuit has been setup for finding. The internal resistance of a given cell. The main battery used a negligible internal resistance. The potentiometer wire itsefl is 4m long. When the resistance, R, connected across the given cell, has value of
(i) Infinity (ii)9.5Ω,
the 'balancing length' , on the potentiometer wire are found to be 3m and 2.85m, respectively.
The value of internal resistance of the cell is
View SolutionThe internal resistance of a cell is determined by using a potentiometer. In an experimetn, an external resistance of 60Ω is used across the given cell. When the key is closed, the balance length on the potentiometer decreases form 72 cm to 60 cm. calculate the internal resistance of the cell.
View Solution
Knowledge Check
3V poteniometer used for the determination of internal resistance of a 2.4V cell. The balanced point of the cell in open circuit is 75.8cm. When a resistor of 10.2Ω is used in the external circuit of the cell the balance point shifts to 68.3cm length of the potentiometer wire. The internal resistance of the cell is
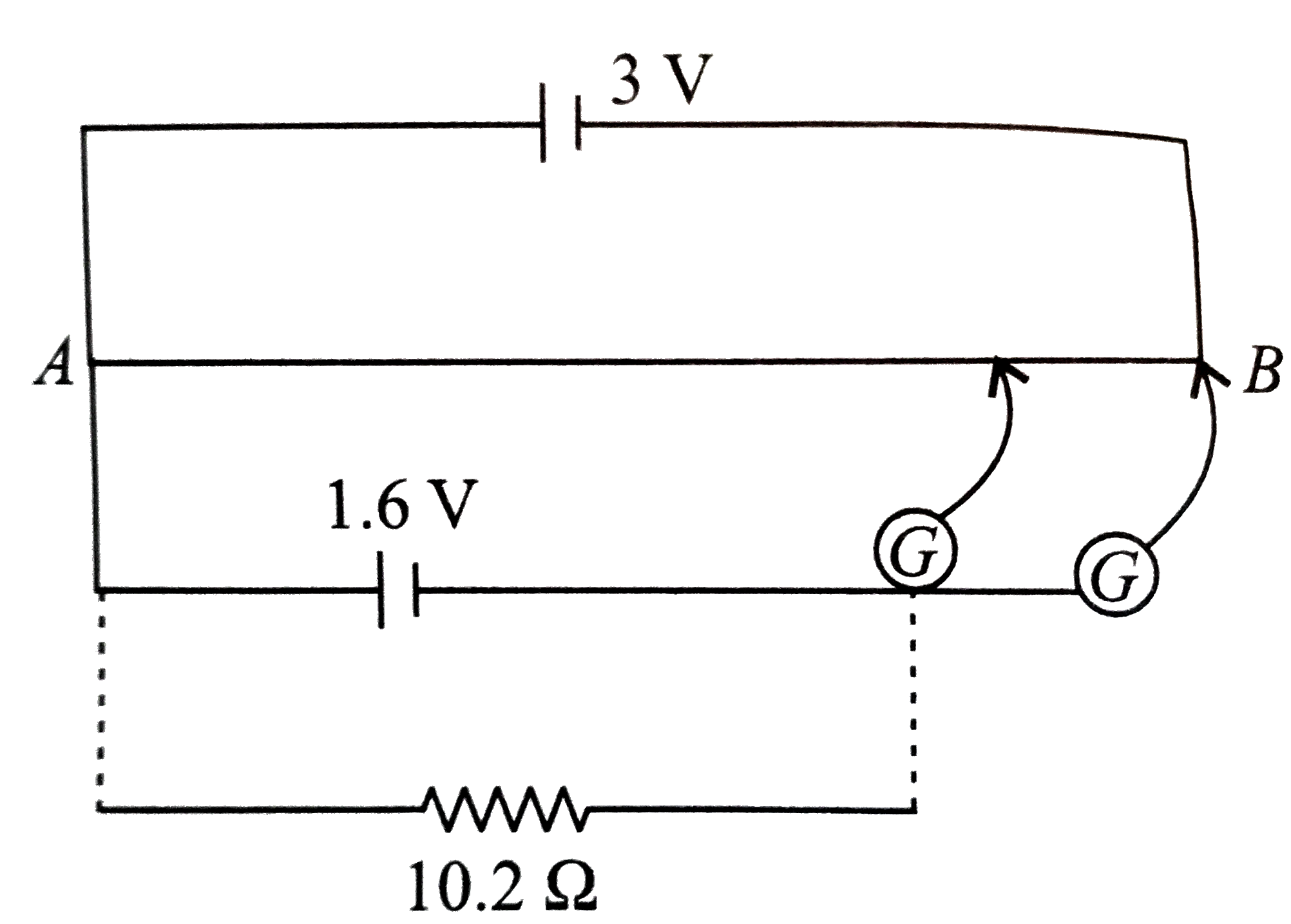 A2.5ΩB2.25ΩC1.12ΩD3.2Ω
A2.5ΩB2.25ΩC1.12ΩD3.2Ω
A potentiometer wire is 10 m long and has a resistance of 18Ω. It is connected to a battery of emf 5 V and internal resistance 2Ω. Calculate the potential gradient along the wire.
View SolutionWhen a Daniel cell is connected in the secondary circuit of a potentiometer, the balancing length is found to be 540 cm. If the balancing length becomes 500 cm. When the cell is short-circuited with 1Ω, the internal resistance of the cell is
View SolutionIf a ideal battery of e.m.f.10 V is connected with external resistance 9Ω and a wire of length 10 m and resistance 1Ω in series as shown. Then the potential gradient of wire is

View SolutionThe wire of potentiometer has resistance 4Ω and length 1m. It is connected to a cell of e.m.f. 2V and internal resistance 1Ω. The current flowing through the potentiometer wire is
View SolutionIn order to determine the internal resistance of a primary cell by means of potentiometer the emf of the battery connected across the ends of the potentiometer wire should be
View SolutionIn an experiment to measure the internal resistance of a cell by a potentiometer, it is found that the balance point is at a length of 2m when the cell is shunted by a 5Ω resistance and is at a length of 3m when the cell is shunted by a 10Ω resistance, the internal resistance of the cell is then
View SolutionTo the potentiometer wire of L and 10Ω resistance, a battery of emf 2.5 volts and a resistance R are connected in series. If a potential difference of 1 volt is balanced across L/2 length, the value of R is Ω will be
View Solution
