Show that time constant (τ=RC) of R−C circuit has the dimensions of time.
Square of time
Square of inverse time
Time
Inverse time
The correct Answer is:C
To show that the time constant τ=RC of an R-C circuit has the dimensions of time, we can follow these steps:
Step 1: Understand the Definitions
- Resistance (R): According to Ohm's law, V=I⋅R, where V is the voltage, I is the current, and R is the resistance. Rearranging gives us:
R=VI
- Capacitance (C): The relationship between charge (Q), capacitance (C), and voltage (V) is given by:
Q=C⋅V⇒C=QV
Step 2: Substitute R and C into the Time Constant Formula
The time constant τ is defined as:
τ=R⋅C
Substituting the expressions for R and C we derived:
τ=(VI)⋅(QV)
Step 3: Simplify the Expression
In the expression τ=(VI)⋅(QV), the V in the numerator and denominator cancels out:
τ=QI
Step 4: Analyze the Units
Now, we need to analyze the units of Q and I:
- The unit of charge Q is Coulombs (C).
- The unit of current I is Amperes (A), which is equivalent to Coulombs per second (C/s).
Thus, we can express the time constant τ as:
τ=QI=CC/s=s
Conclusion
The unit of τ is seconds (s), which is indeed a unit of time. Therefore, we have shown that the time constant τ=RC has the dimensions of time.
- Resistance (R): According to Ohm's law, V=I⋅R, where V is the voltage, I is the current, and R is the resistance. Rearranging gives us:
R=VI
Q=C⋅V⇒C=QV
The time constant τ is defined as:
τ=R⋅C
Substituting the expressions for R and C we derived:
τ=(VI)⋅(QV)
In the expression τ=(VI)⋅(QV), the V in the numerator and denominator cancels out:
τ=QI
Now, we need to analyze the units of Q and I:
- The unit of charge Q is Coulombs (C).
- The unit of current I is Amperes (A), which is equivalent to Coulombs per second (C/s).
τ=QI=CC/s=s
The unit of τ is seconds (s), which is indeed a unit of time. Therefore, we have shown that the time constant τ=RC has the dimensions of time.
Topper's Solved these Questions
- UNITS AND MEASUREMENTSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - UNITS AND MEASUREMENTSEXERCISE - ASSIGNMENT (SECTION - D)
15 Videos
- UNITS AND MEASUREMENTSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - UNITS AND MEASUREMENTSEXERCISE - ASSIGNMENT (SECTION - B)
31 Videos
- THERMODYNAMICSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - ASSIGNMENT (SECTION -D) (Assertion - Reason Type Questions)
10 Videos
- WAVE OPTICSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Assignment (Section-J (Aakash Challengers question))
1 Videos
Similar Questions
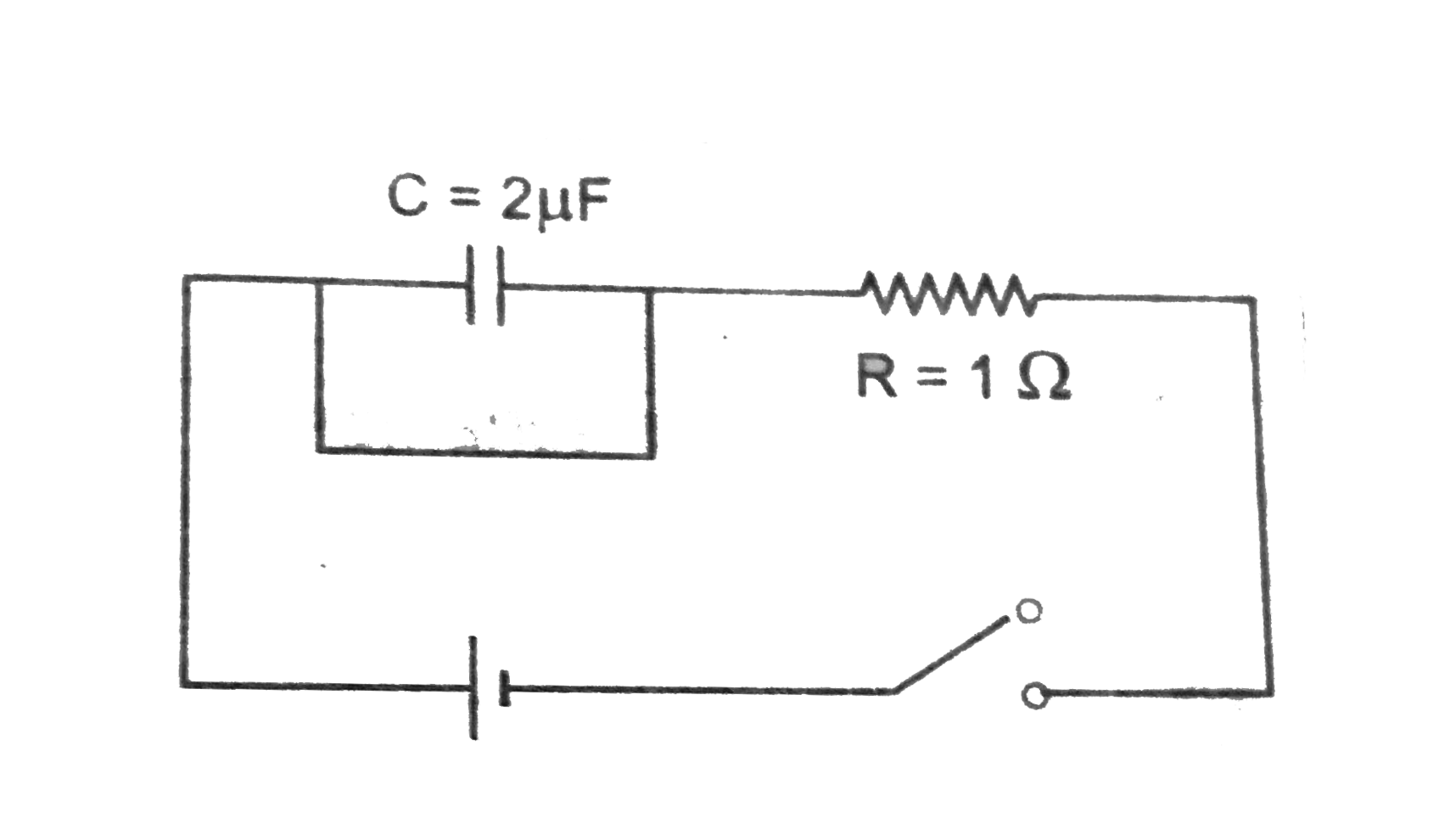
The capacitive time constant of the RC circuit shown in the figure.
View SolutionDefine time constant of an RC circuit. What is its SI unit?
View SolutionGas constant 'R' has dimensions :
View SolutionA capacitor C is connected to two equal resistances as shown in the figure. Consider the following statemets
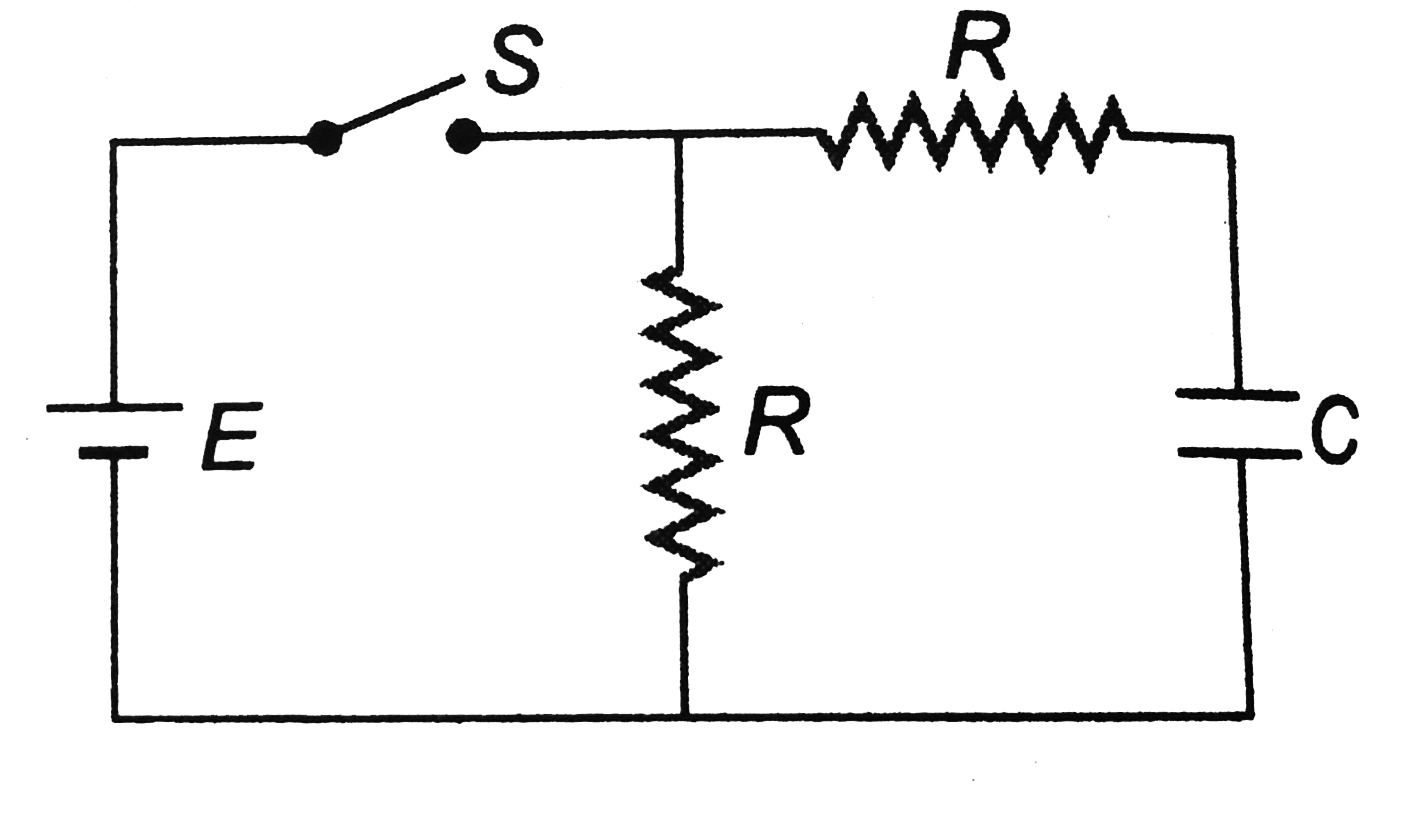
i. At the time of charging of capacitor time constant of the circuit is CR
ii. At the time of discharging of the capacitor the time constant of the circuit is CR
iii. At the time of discharging of the capacitor the time constant of the circuit is 2CR
iv At the time of charging of the capacitor the time constant of the circuit is 2CR
View SolutionThe time constant of C-R circuit is
View SolutionFor L-R circuit, the time constant is equal to
View SolutionShow that LR has units of time.
View SolutionThe time constant of the circuit shown in the figure is
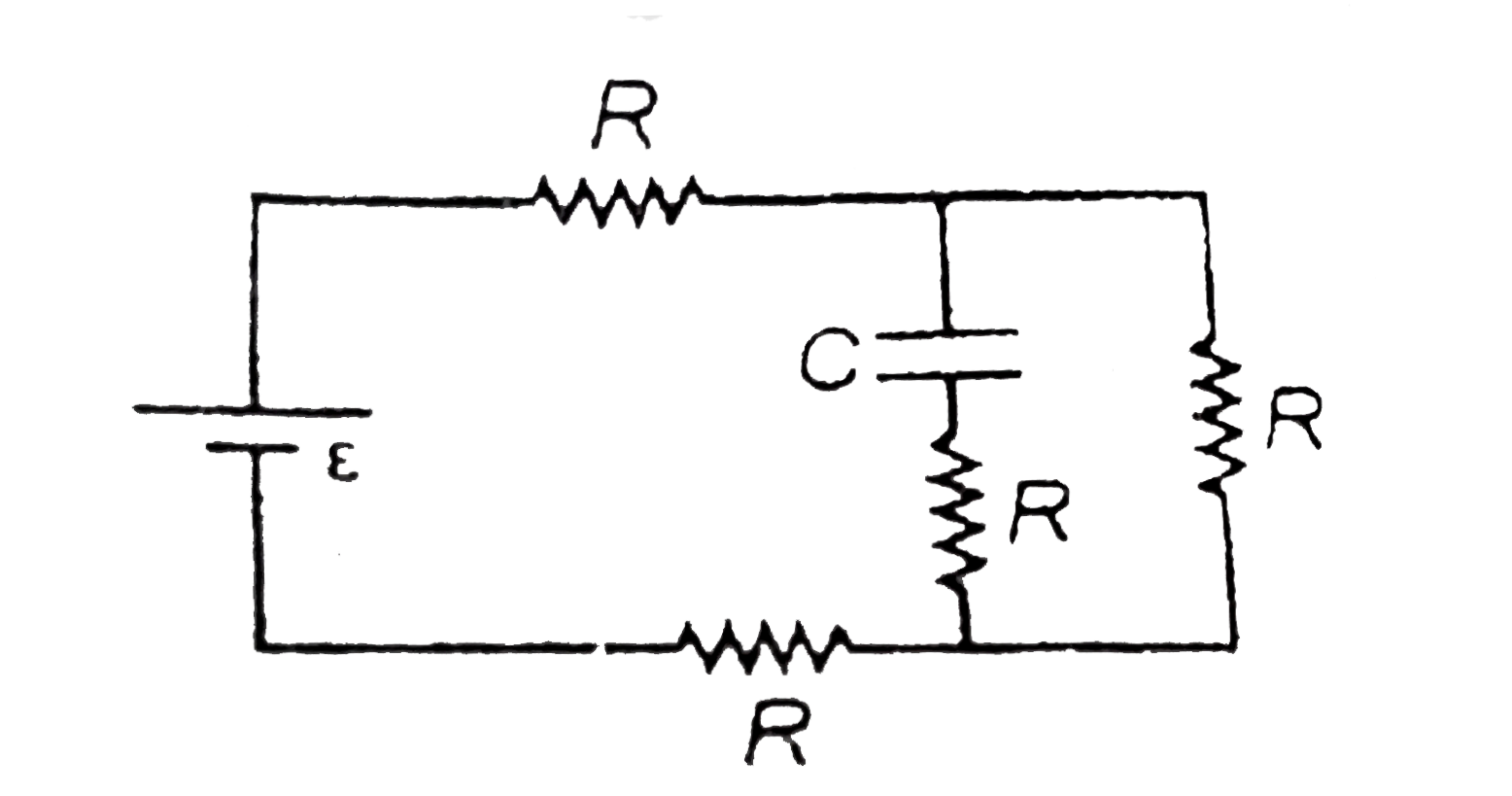
View SolutionThe time constant of charging of the circuit shown in figure is

View SolutionThe current in a discharging LR circuit is given by I=i0(tτ) where τ is the time constant of the circuit. Calculate the rms current for the period t=0 to t=τ.
View Solution
