For L-R circuit, the time constant is equal to
twice the ratio of the energy stored in the magnetic field to the ratio of dissipation of energy in the resistance
the ratio of the energy stored in the magnetic field to the ratio of dissipation of energy in the resistance
half of the ratio of the energy stored in the magnetic field to the ratio of dissipation of energy in the resistance
square of the ratio of the energy stored in the magnetic field to the ratio of dissipation of energy in the resistance
The correct Answer is:A
To solve the question regarding the time constant of an L-R circuit, we will follow these steps:
Step 1: Understand the Time Constant in an L-R Circuit
The time constant (τ) in an L-R circuit is defined as the ratio of inductance (L) to resistance (R). The formula is given by:
τ=LR
Step 2: Identify the Energy Stored in the Circuit
The energy stored in the magnetic field of an inductor is given by the formula:
Energy stored in magnetic field=12LI2
where I is the current flowing through the circuit.
Step 3: Identify the Energy Dissipated in the Resistance
The energy dissipated in the resistance (as heat) can be expressed as:
Energy in resistance=I2R
Step 4: Formulate the Ratio of Energies
Now, we can find the ratio of the energy stored in the magnetic field to the energy dissipated in the resistance:
Ratio=Energy stored in magnetic fieldEnergy in resistance=12LI2I2R
Step 5: Simplify the Ratio
When we simplify this ratio, the I2 terms cancel out:
Ratio=12LR=L2R
Step 6: Relate the Ratio to the Time Constant
From our earlier step, we know that the time constant is:
τ=LR
Thus, we can express the ratio in terms of the time constant:
Ratio=τ2
Step 7: Identify the Correct Option
The question asks for the time constant in terms of the energy ratio. Since we derived that the ratio of the energy stored in the magnetic field to the energy dissipated in the resistance is L2R, we can conclude that:
Time constant=2×Ratio
Thus, the correct option is:
Twice the ratio of energy stored in the magnetic field to the ratio of dissipation of energy in the resistance.
Final Answer
The time constant for an L-R circuit is equal to:
τ=LR
And the correct option is:
Twice the ratio of energy stored in the magnetic field to the ratio of dissipation of energy in the resistance.
---
The time constant (τ) in an L-R circuit is defined as the ratio of inductance (L) to resistance (R). The formula is given by:
τ=LR
The energy stored in the magnetic field of an inductor is given by the formula:
Energy stored in magnetic field=12LI2
where I is the current flowing through the circuit.
The energy dissipated in the resistance (as heat) can be expressed as:
Energy in resistance=I2R
Now, we can find the ratio of the energy stored in the magnetic field to the energy dissipated in the resistance:
Ratio=Energy stored in magnetic fieldEnergy in resistance=12LI2I2R
When we simplify this ratio, the I2 terms cancel out:
Ratio=12LR=L2R
From our earlier step, we know that the time constant is:
τ=LR
Thus, we can express the ratio in terms of the time constant:
Ratio=τ2
The question asks for the time constant in terms of the energy ratio. Since we derived that the ratio of the energy stored in the magnetic field to the energy dissipated in the resistance is L2R, we can conclude that:
Time constant=2×Ratio
Thus, the correct option is:
Twice the ratio of energy stored in the magnetic field to the ratio of dissipation of energy in the resistance.
The time constant for an L-R circuit is equal to:
τ=LR
And the correct option is:
Twice the ratio of energy stored in the magnetic field to the ratio of dissipation of energy in the resistance.
Topper's Solved these Questions
Similar Questions
During current growth in an L-R circuit the time constant is the time in which the magnitude of current becomes
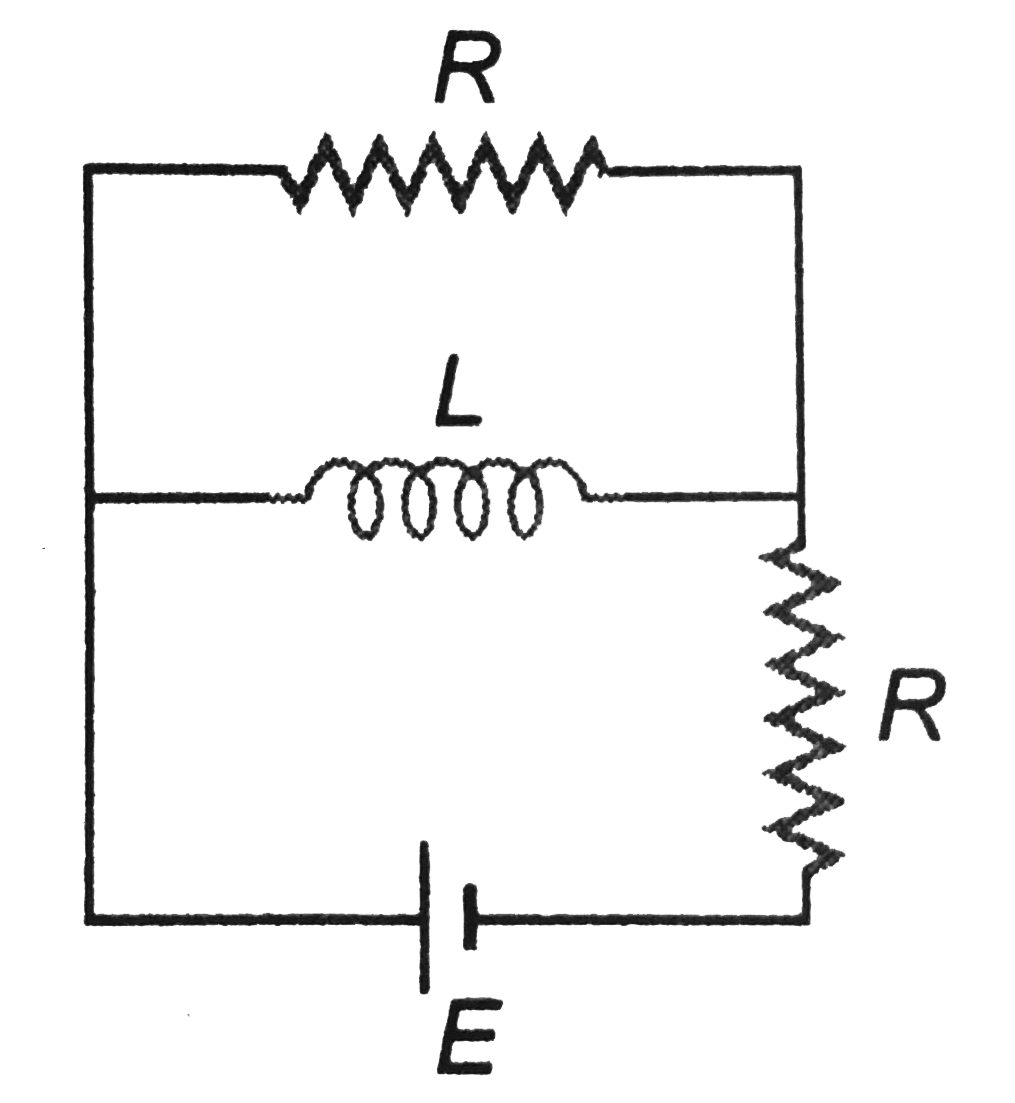
View SolutionThe figure shows an L−R circuit the time constant for the circuit is
View SolutionA current i0 is flowing through an L−R circuit of time constant t0. The source of the current is switched off at time t=0. Let r be the value of (−di/dt) at time t=0.Assuming this rate to be constant, the current will reduce to zero in a time interval of
View SolutionWhen a capacitor discharges through a resistance R, the time constant is τ and the maximum current in the circuit is i0. Then,
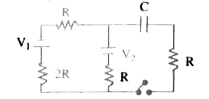
View SolutionIn the transient circuit shown, the time constant of the circuit is :
View SolutionIn a decaying L−R circuit, the time after which energy stores in the inductor reduces to one fourth of its initial values is
View SolutionThe time constant of C-R circuit is
View SolutionIn the circuit shown in fig, the time constant of the two braches are equal(=T). Then if the key S is closed at the instant t=0, the time in which the current in the circuit through the battery will rise to its final value of (E/R) will be, (assume that the internal resistance of the battery and of the connecting wire are negligible)

View SolutionGiven L1=1mH, R1=1Ω, L2=2mH, R2=2Ω
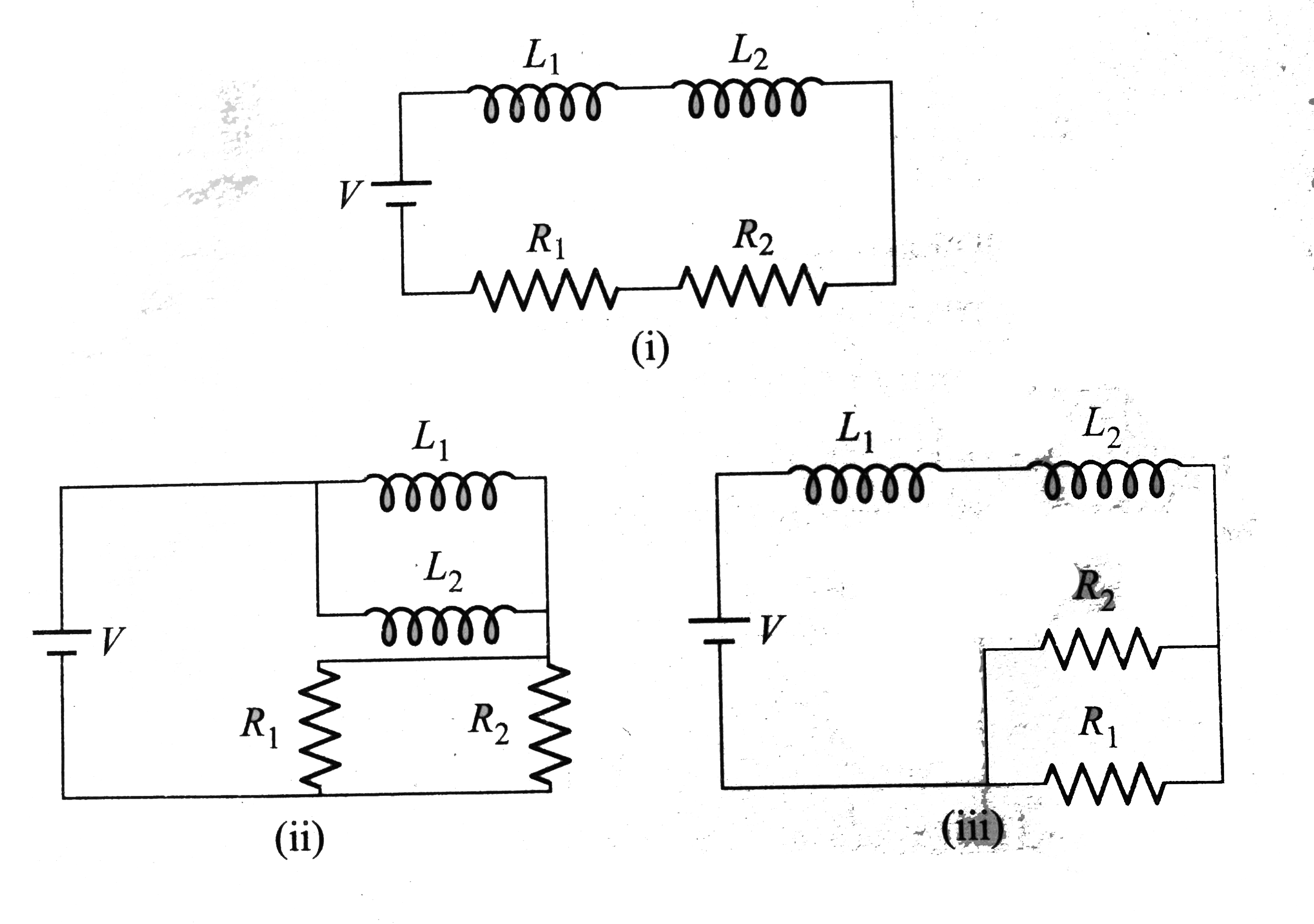
Neglecting mutual inductance, the time constants (in ms) for circuits (i), (ii), and (iii) are
View SolutionIf for above circuit the capacitive reactance is two times of inductive Reactance, and resistance R is equal to inductance Reactance then power factor of circuit is .

View Solution
