In L-C oscillation, maximum charge on capacitor can be Q. If at any instant, electric energy and magnetic enegy associated with circuit is equal, then charge on capacitor at the anstant is
Q√2
Q2
√3Q2
3Q2
The correct Answer is:A
To solve the problem step by step, let's break down the concepts involved in LC oscillation and the relationship between electric and magnetic energy in the circuit.
1. Understanding the Maximum Charge (Q):
- The maximum charge that the capacitor can store is given as Q.
2. Energy Stored in the Capacitor:
- The electric energy (UE) stored in the capacitor when it has charge q is given by the formula:
UE=12q2C
- Here, C is the capacitance of the capacitor.
3. Energy Stored in the Inductor:
- The magnetic energy (UB) stored in the inductor when the current is I is given by:
UB=12LI2
- Here, L is the inductance of the inductor.
4. Condition Given in the Problem:
- It is given that at a certain instant, the electric energy and magnetic energy are equal:
UE=UB
5. Expressing Magnetic Energy in Terms of Charge:
- In LC oscillation, the current I can be related to the charge q on the capacitor as:
I=−dqdt
- At the instant when electric energy equals magnetic energy, we can express UB in terms of the charge q.
6. Total Energy in the Circuit:
- The total energy in the LC circuit is constant and equals the maximum energy stored in the capacitor when it is fully charged:
Utotal=12Q2C
7. Setting Up the Equation:
- Since UE=UB, we can write:
UE+UB=Utotal
- Substituting UE=UB into the equation gives:
2UE=Utotal
- Therefore:
2(12q2C)=12Q2C
8. Simplifying the Equation:
- This simplifies to:
q2=Q22
9. Finding the Charge q:
- Taking the square root of both sides gives:
q=Q√2
10. Conclusion:
- The charge on the capacitor at the instant when the electric energy equals the magnetic energy is:
q=Q√2
Final Answer:
The charge on the capacitor at the instant when electric energy and magnetic energy are equal is Q√2.
- The maximum charge that the capacitor can store is given as Q.
- The electric energy (UE) stored in the capacitor when it has charge q is given by the formula:
UE=12q2C
- Here, C is the capacitance of the capacitor.
- The magnetic energy (UB) stored in the inductor when the current is I is given by:
UB=12LI2
- Here, L is the inductance of the inductor.
- It is given that at a certain instant, the electric energy and magnetic energy are equal:
UE=UB
- In LC oscillation, the current I can be related to the charge q on the capacitor as:
I=−dqdt
- At the instant when electric energy equals magnetic energy, we can express UB in terms of the charge q.
- The total energy in the LC circuit is constant and equals the maximum energy stored in the capacitor when it is fully charged:
Utotal=12Q2C
- Since UE=UB, we can write:
UE+UB=Utotal
- Substituting UE=UB into the equation gives:
2UE=Utotal
- Therefore:
2(12q2C)=12Q2C
- This simplifies to:
q2=Q22
- Taking the square root of both sides gives:
q=Q√2
- The charge on the capacitor at the instant when the electric energy equals the magnetic energy is:
q=Q√2
The charge on the capacitor at the instant when electric energy and magnetic energy are equal is Q√2.
Similar Questions
Knowledge Check
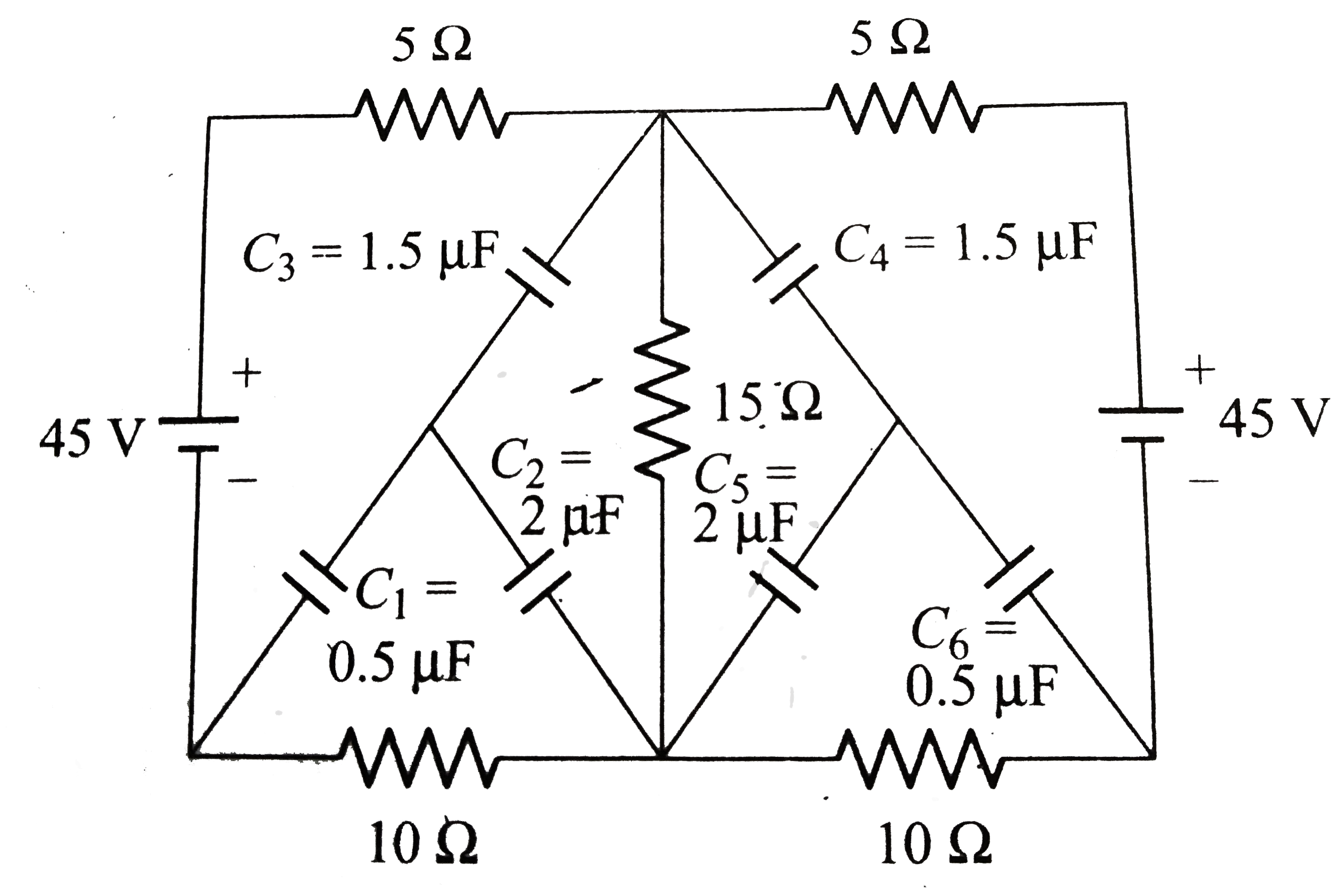
In the circuit given, the charge on capacitor C3 at steady state is
 A6μCB12μCC18μCD24μC
A6μCB12μCC18μCD24μC
The circuit is in a steady state.
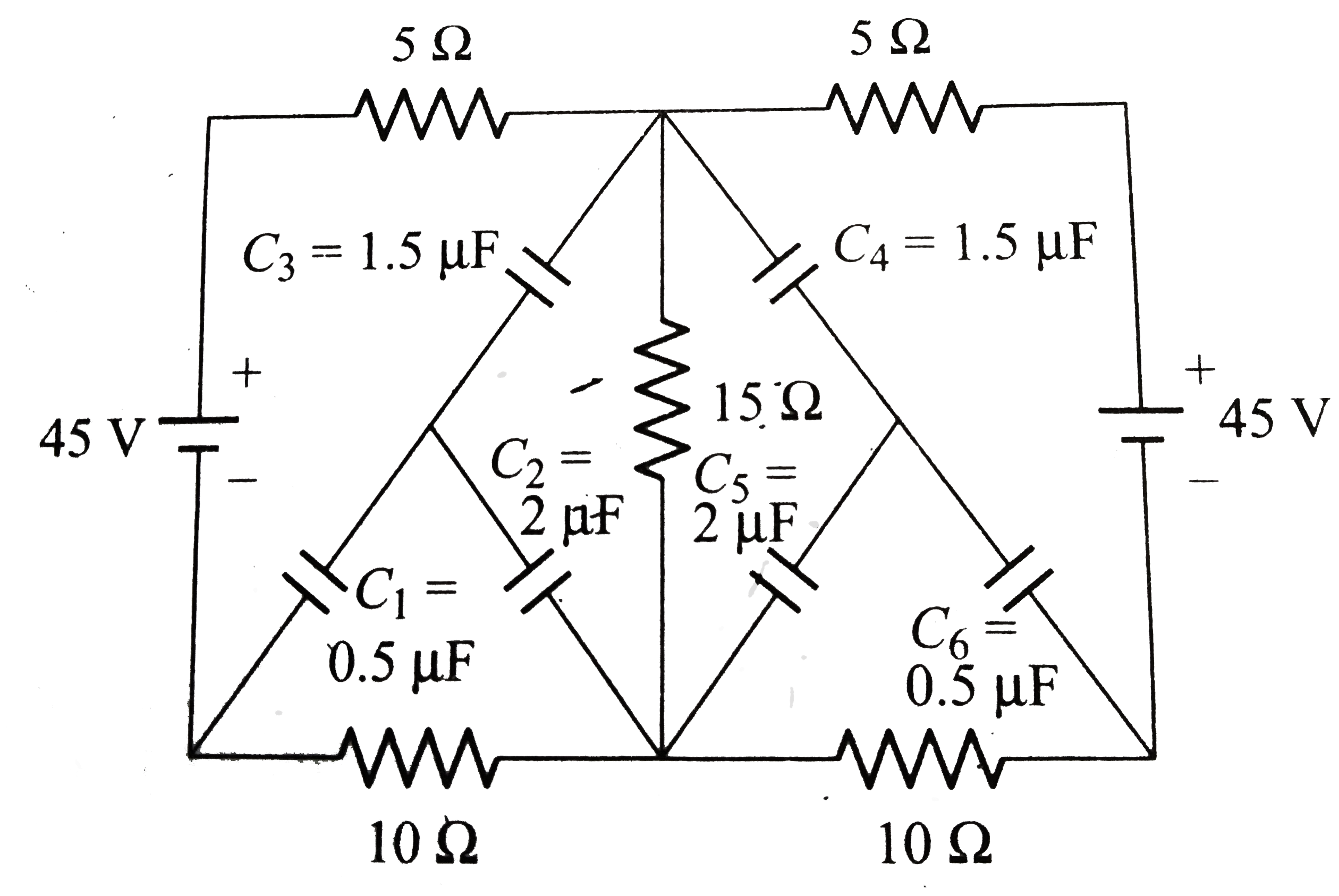
The charge in capacitor C1 is
View SolutionThe circuit is in a steady state.
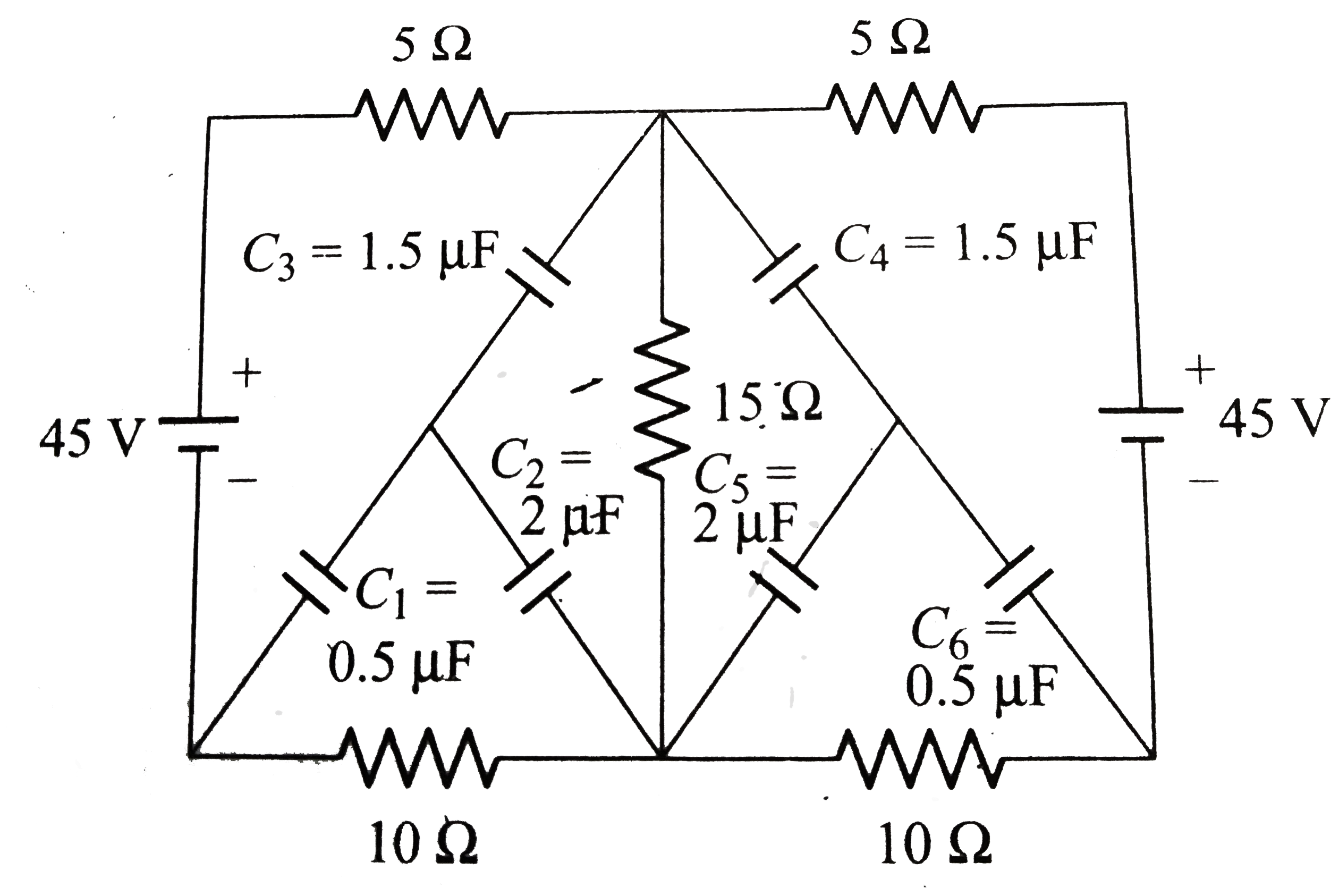
The charge in capacitor C2 is
View SolutionThe switch S in the circuit diagram is closed at t = 0. The charge on capacitors at any time is
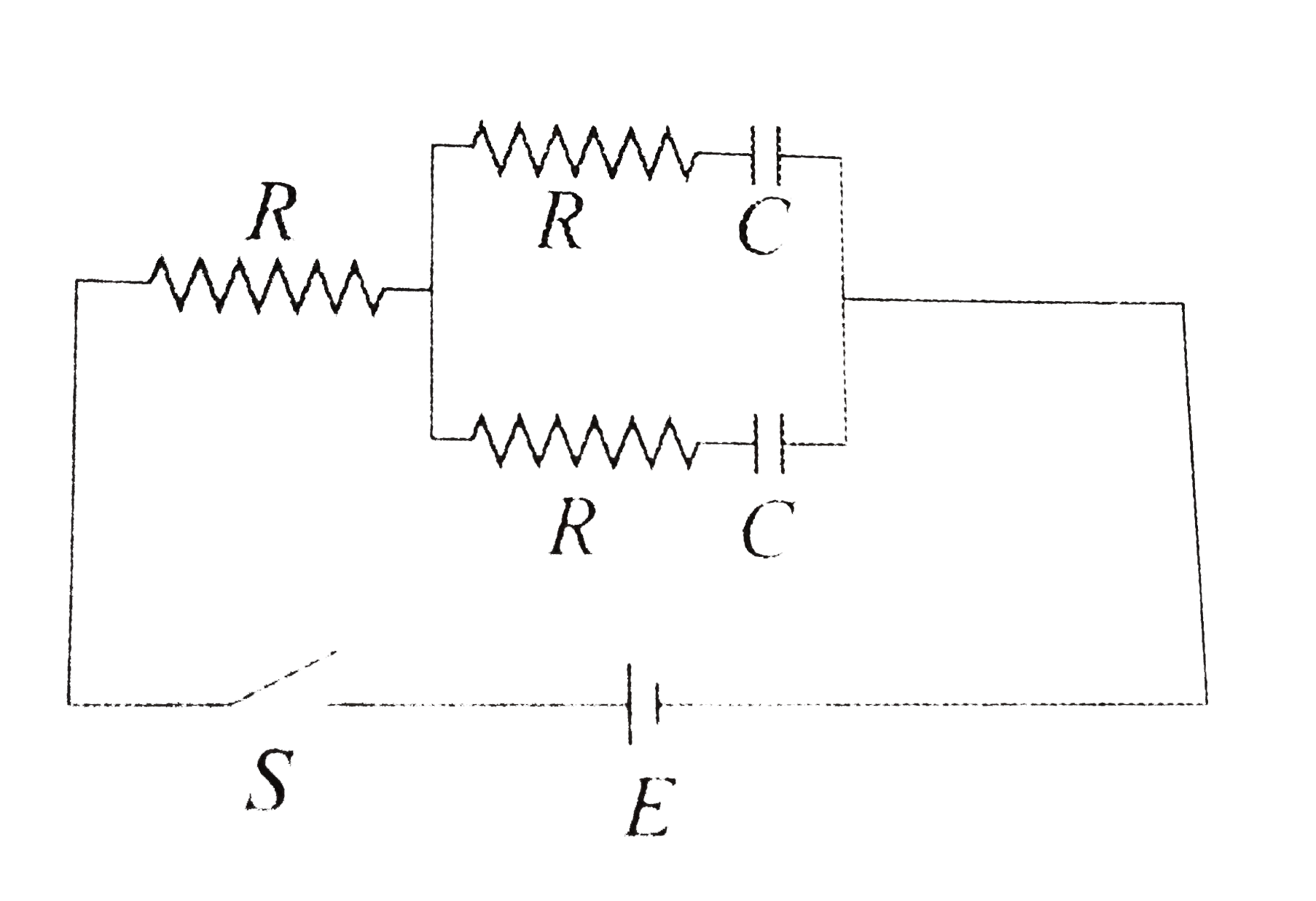
View SolutionThe capacitance of a charged capacitor is C and the energy stored in it is U. What is the value of charge on the capacitor?
View SolutionIn an oscillating LC circuit the maximum charge on the capacitor is Q. The charges on the capacitor when the energy is stored equally between the electric and magnetic field is
View SolutionIn an oscillating LC circuit the maximum charge on the capacitor is Q. The charges on the capacitor when the energy is stored equally between the electric and magnetic field is
View SolutionA capacitor is connected across an inductor. At time t = 0 charge on the capacitor is equal to 1√2qmax, where qmax is the maximum charge on the capacitor. The time t, at which the energy stored in the capacitor is equal to the energy stored in the inductor is (The inductance of the inductor is L and capacitance of the capacitor is C. Resistance of the circuit is zero)
View Solution