A microscope is focussed on a coin lying at the bottom of a beaker. The microscope is now raised up by . To what depth should the water be poured into the beaker so that coin is again in focus ? (Refration index of water is )
1 cm
cm
3 cm
4 cm
The correct Answer is:D
To solve the problem, we need to determine how deep the water should be poured into the beaker so that the coin is again in focus after the microscope has been raised by 1 cm.
1. Understanding the Situation:
- Initially, the microscope is focused on a coin at the bottom of the beaker.
- When the microscope is raised by 1 cm, the coin will appear blurred because the distance from the microscope to the coin has increased.
2. Apparent Shift of the Coin:
- To bring the coin back into focus, we need to account for the apparent shift caused by the refraction of light in water.
- The apparent height (H') of the coin when viewed through water is given by the formula:
H′=H(1−1n)
where H is the actual depth of the coin and n is the refractive index of water.
3. Setting Up the Equation:
- Since the microscope is raised by 1 cm, we want the apparent height of the coin to increase by 1 cm as well:
H′=1 cm
- Therefore, we can set up the equation:
1=H(1−1n)
4. Substituting the Refractive Index:
- The refractive index of water is given as n=43.
- Substituting this into the equation gives:
1=H⎛⎝1−143⎞⎠
- Simplifying the term inside the parentheses:
1−143=1−34=14
5. Solving for H:
- Now substituting this back into the equation:
1=H(14)
- To find H, we rearrange the equation:
H=1×4=4 cm
6. Conclusion:
- Therefore, the depth of water that should be poured into the beaker to bring the coin back into focus is 4 cm.
Final Answer:
The depth of water to be poured into the beaker is 4 cm.
---
- Initially, the microscope is focused on a coin at the bottom of the beaker.
- When the microscope is raised by 1 cm, the coin will appear blurred because the distance from the microscope to the coin has increased.
- To bring the coin back into focus, we need to account for the apparent shift caused by the refraction of light in water.
- The apparent height (H') of the coin when viewed through water is given by the formula:
H′=H(1−1n)
where H is the actual depth of the coin and n is the refractive index of water.
- Since the microscope is raised by 1 cm, we want the apparent height of the coin to increase by 1 cm as well:
H′=1 cm
- Therefore, we can set up the equation:
1=H(1−1n)
- The refractive index of water is given as n=43.
- Substituting this into the equation gives:
1=H⎛⎝1−143⎞⎠
- Simplifying the term inside the parentheses:
1−143=1−34=14
- Now substituting this back into the equation:
1=H(14)
- To find H, we rearrange the equation:
H=1×4=4 cm
- Therefore, the depth of water that should be poured into the beaker to bring the coin back into focus is 4 cm.
The depth of water to be poured into the beaker is 4 cm.
Topper's Solved these Questions
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - ASSIGNMENT (SECTION - B)
35 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - ASSIGNMENT (SECTION - C)
80 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - EXERCISE
45 Videos
- PHYSICAL WORLDBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - PHYSICAL WORLDEXERCISE - ASSIGNMENT (Section-B)
4 Videos
- SEMICONDUCTOR ELECTRONICS (MATERIAL, DEVICES AND SIMPLE CIRUITS )BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SEMICONDUCTOR ELECTRONICS (MATERIAL, DEVICES AND SIMPLE CIRUITS )EXERCISE - Assignment SECTION - D (Assertion & reason type Question)
10 Videos
Similar Questions
Knowledge Check
A microscope is focused on a mark on a piece of paper and then a slab of glass of thickness 3cm and refractive index 1.5 is placed over the mark. How should the microscope be moved to get the mark in focus again ?
A4.5cm downwardB1cm downwardC2cm downwardD1cm upward
Assertion A diverging lens (in air) cannot be made more diverging whatever be the medium we choose completely immerse the lens.
Reason The minimum refractive index of any medium is 1.
View SolutionA travelling microscope is focussed on to a scratch on the bottom of a beaker. Water of refractive index 43 is poured in it. Then the microscope is to be lifted through 2 cm focus it again. Find the depth of water in the beaker.
View SolutionA microscope is focussed on a point object, and then its objective is raised through a height of 2cm when a glass slab of refractive index 1.5 is placed over this point object such that it is focussed again. The thickness of the glass slab is
View SolutionA microscope is focused on a mark on a piece of paper and then a slab of glass of thickness 3cm and refractive index 1.5 is placed over the mark. How should the microscope be moved to get the mark in focus again ?
View SolutionA coin is placed at the bottom of a beaker containing water (refractive index=4/3) at a depth of 12cm. By what height the coin appears to be raised when seen from vertical above ?
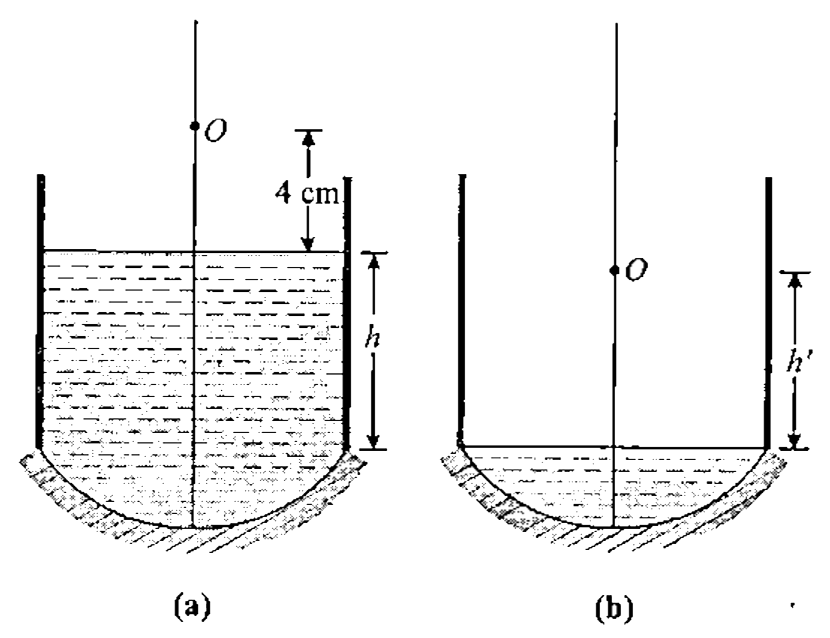
View SolutionA beaker is filled with water as shown in figure (a). The bottom surface of the beaker is a concave mirror of large radius of curvature and small aperture. The height of water is h=40cm. It is found that when an object is placed 4 cm above the water surface, the image coincides with the object. Now the water level h is reduced to zero but there will still be some water left in the concave part of the mirror as shown in figure (b). The new height of the object h' above the new water surface so that the image again coincides with the object, will be (Refractive index of water =4/3)
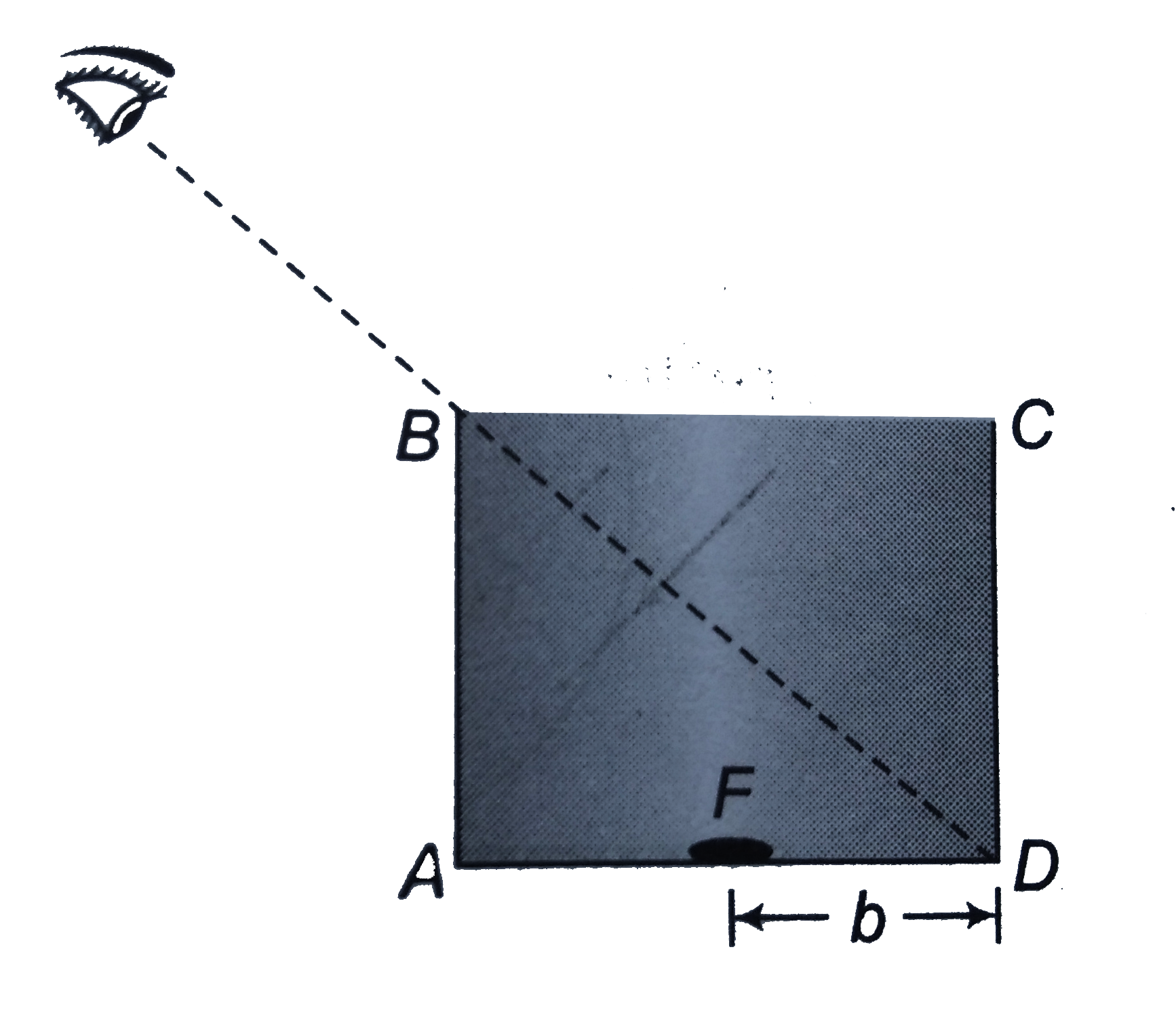
View SolutionA cubical vessel with non-transparent walls is so located that the eye of an observer does not see its bottom but sees all of the wall CD.
To what height should water be poured into the vessel for the observer to see an object F arranged at a distance of b=10cm from corner D? The face of the vessel is a=40cm. Refractive index of water is 43.
View Solution
