A small coin is resting on the bottom of a beaker filled with a liquid. A ray of light from the coin travels upto the surface of the liquid and moves along its surface (see figure)

How fast is the light traveling in the liquid ?
1.2×108m/s
1.8×108m/s
1.3×108m/s
3.0×108m/s
The correct Answer is:B
Step by step video & image solution for A small coin is resting on the bottom of a beaker filled with a liquid. A ray of light from the coin travels upto the surface of the liquid and moves along its surface (see figure) How fast is the light traveling in the liquid ? by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - ASSIGNMENT (SECTION - D)
16 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - ASSIGNMENT (SECTION - B)
35 Videos
- PHYSICAL WORLDBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - PHYSICAL WORLDEXERCISE - ASSIGNMENT (Section-B)
4 Videos
- SEMICONDUCTOR ELECTRONICS (MATERIAL, DEVICES AND SIMPLE CIRUITS )BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SEMICONDUCTOR ELECTRONICS (MATERIAL, DEVICES AND SIMPLE CIRUITS )EXERCISE - Assignment SECTION - D (Assertion & reason type Question)
10 Videos
Similar Questions
A small coin is resting on the bottom of a beaker filled with a liquid. A ray of light from the coin travels up to the surface of the liquid and moves along its surface (see figure ).
How fast is the light travelling in the liquid ?

View SolutionA metal coin at the bottom of a beaker filled with a liquid of refractive index 4/3 to height of 6cm. To an observer looking from above the surface of the liquid, coin will appear at a depth of (consider paraxial rays).
View Solution
Knowledge Check
A hemispherical portion of a radius R is removed from the bottom of a cylinder of radius R. The volume of the remaining cylinder is V and its mass is M. It is suspended by a string in a liquid of density ρ where it stays vertical . The upper surface of the cylinder is at a depth of h below the liquid surface. THe force on the bottom of the cylinder by the liquid is
AM gBMg−Vρ gCMg+ΠR2hgρDρg(V+ΠR2h)
A beaker is filled with a liquid of density ρ upto a height h If the beaker is at rest, the mean pressure at the walls is:
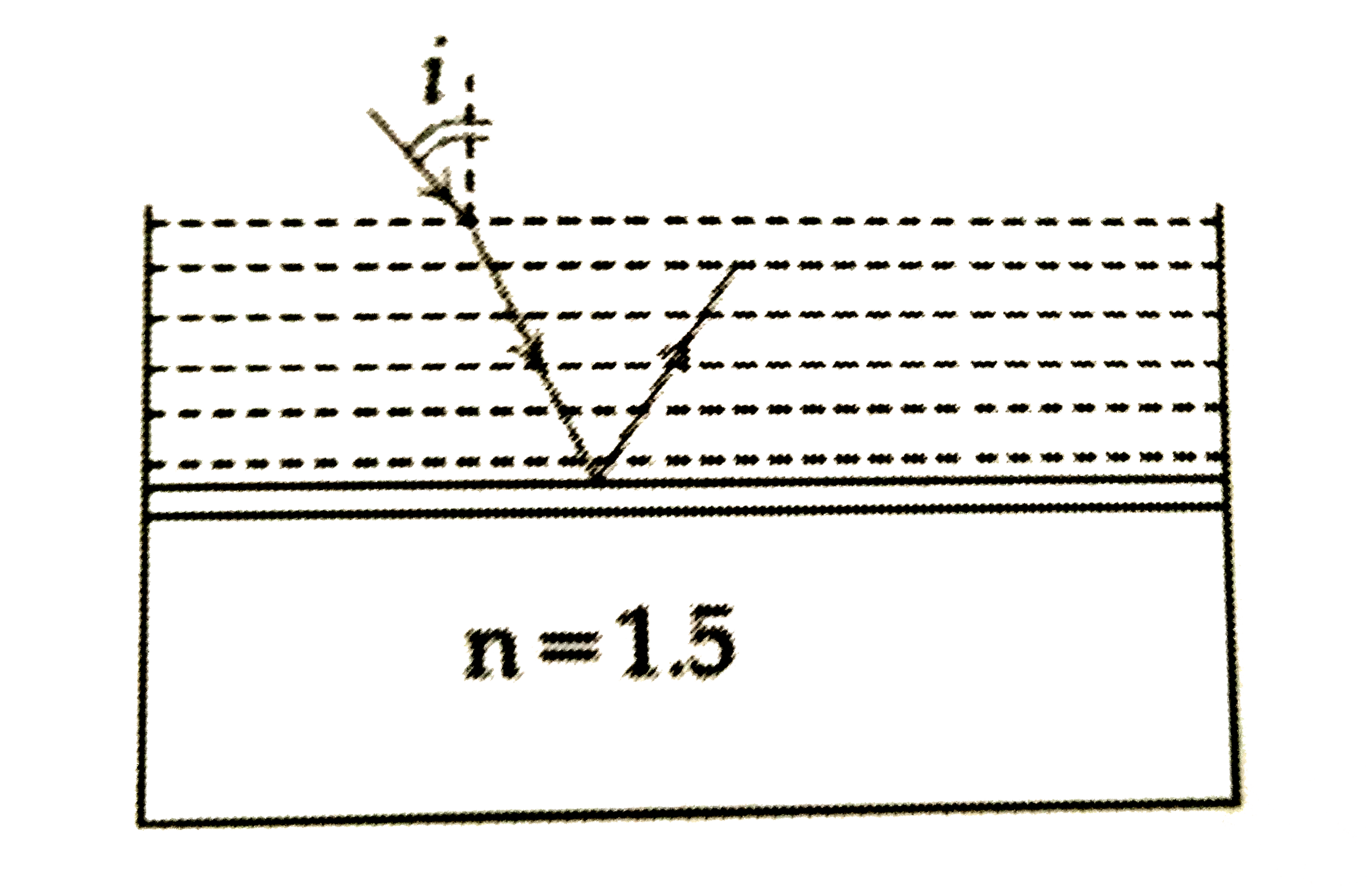
View SolutionConsider a tank made of glass (refractive index 1.5) with a thick bottom. It is filled with a liquid of refractive index μ. A student finds that, irrespective of what the incident angle I (see figure) is for a beam of light entering the liquid, the light reflected from the liquid glass interface is never completely polarized. For this to happen, the minimum value of μ is :
View SolutionA container of width 2a is filled with a liquid. A thin wire of weight per unit length λ is gently placed over the liquid surface in the middle of the surface as shown in the figure. As a result, the liquid surface is depressed by a distance y(y<<a). If the surface tension of the liquid is 4λagky. Then value of k is .

View SolutionA disc is placed on the surface of pond filled with liquid of refractive index 53. A source of light is placed 4m below the surface of liquid. Calculate the minimum area of the disc so that light does not come out of liquid.
View SolutionA rectangular tank filled with some liquid is accelerated along a horizontal surface at 403ms−2. Inside the liquid, a laser pointer is fixed a the centre of the tank which shoots a thin laser beam in the vertically upward direction. If after refraction from the liquid surface, the laser beam moves along the surface of the liquid, then what is the refrctive index of the liquid ?
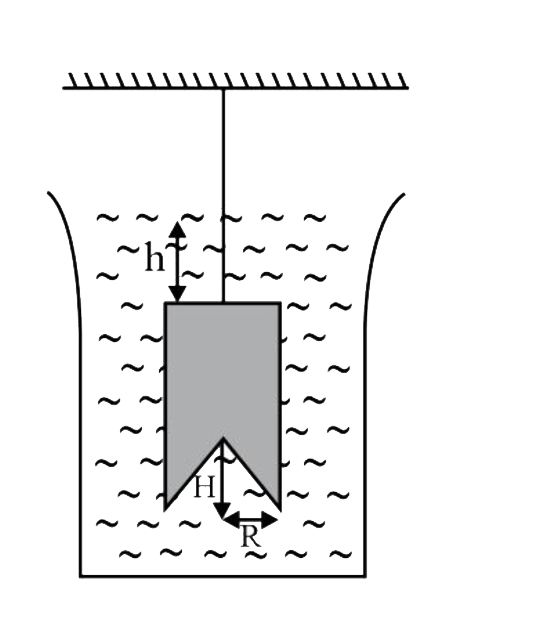
View SolutionA conical portion of radius R and height H is removed from the bottom of a cylinder of radius R. The volume of the remaining cylinder is V and its mass is M. It is suspended by a string in a liquid of density ρ where it stays vertical . The upper surface of the cylinder is at depth h below the liquid surface . The force on the bottom of the cylinder by the liquid is
View SolutionDensity of a liquid varies with depth as ρ=αh. A small ball of density ρ0 is released from the free surface of the liquid. Then
View Solution
