A: A bar magnet does not exert a torque on itself due to its own field.
R: One element of a current-carrying non-straight wire exert a force on another element of the same wire.
If both Assertion & Reason are the true and the reason is the correct explanation of the assertion, then mark (1)
If both Assertion & Reason are true but the reson is not the correct explanation of the assertion, then mark (2)
If Assertion is true statement but Reason is false, then mark (3)
If both Assertion and Reason are false statements, then mark (4)
The correct Answer is:B
To analyze the given assertion and reason, let's break down the statements step by step.
Step 1: Evaluate the Assertion
Assertion: A bar magnet does not exert a torque on itself due to its own field.
- A bar magnet has two poles: a North pole and a South pole. The magnetic field produced by the magnet interacts with the magnet itself.
- However, the forces acting on the different parts of the magnet due to its own magnetic field result in equal and opposite torques that cancel each other out.
- Therefore, the net torque acting on the bar magnet due to its own field is zero.
Conclusion for Assertion: The assertion is true.
Step 2: Evaluate the Reason
Reason: One element of a current-carrying non-straight wire exerts a force on another element of the same wire.
- In a current-carrying wire, each segment of the wire generates a magnetic field around it.
- According to Ampère's law, a current-carrying conductor experiences a force due to the magnetic field created by other current-carrying segments.
- Thus, one segment (or element) of the wire does exert a force on another segment of the same wire.
Conclusion for Reason: The reason is also true.
Step 3: Determine the Relationship Between Assertion and Reason
- Both the assertion and the reason are true statements.
- However, they pertain to different topics: the assertion is about the behavior of a bar magnet in its own field, while the reason discusses the interaction between elements of a current-carrying wire.
Final Conclusion
- The assertion is true, and the reason is true, but the reason does not explain the assertion. Therefore, the correct option is that both statements are true, but the reason does not explain the assertion.
---
Assertion: A bar magnet does not exert a torque on itself due to its own field.
- However, the forces acting on the different parts of the magnet due to its own magnetic field result in equal and opposite torques that cancel each other out.
- Therefore, the net torque acting on the bar magnet due to its own field is zero.
Reason: One element of a current-carrying non-straight wire exerts a force on another element of the same wire.
- According to Ampère's law, a current-carrying conductor experiences a force due to the magnetic field created by other current-carrying segments.
- Thus, one segment (or element) of the wire does exert a force on another segment of the same wire.
- Both the assertion and the reason are true statements.
- However, they pertain to different topics: the assertion is about the behavior of a bar magnet in its own field, while the reason discusses the interaction between elements of a current-carrying wire.
- The assertion is true, and the reason is true, but the reason does not explain the assertion. Therefore, the correct option is that both statements are true, but the reason does not explain the assertion.
Topper's Solved these Questions
- MAGNETISM AND MATTER BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - ASSIGNMENT (SECTION C)
34 Videos
- LAWS OF MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Assignment (SECTION-D) (Assertion-Reason Type Questions)
15 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - SECTION - J
9 Videos
Similar Questions
The magnetic field in a straight current carrying conductor wire is:
View SolutionMagnitude of magnetic field at a point P due to a current carrying wire, starting from origin and expanded to y-axis is
View Solutionthe force on current carrying wire placed in uniform magnetic field B as shown in figure is
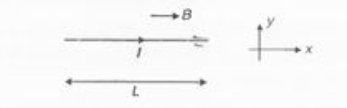
View SolutionThe net charge in a current carrying wire is zero. Them, why does a magnetic field exert a force on it?
View SolutionFind the direction of magnetic field at a point P due to two infinite current carrying wires shown in the figure below

View SolutionFind the magnitude and direction of magnetic field at point P due to the current carrying wire as shown in

View SolutionA long straight wire AB carries a current of 4 A. A proton P travels at 4×106ms−1 parallel to the wire 0.2 m from it and in a direction opposite to the current as shown in the figure. Calculate the force which the magnetic field due to the current carrying wire exerts on the proton. Also specify its direction.
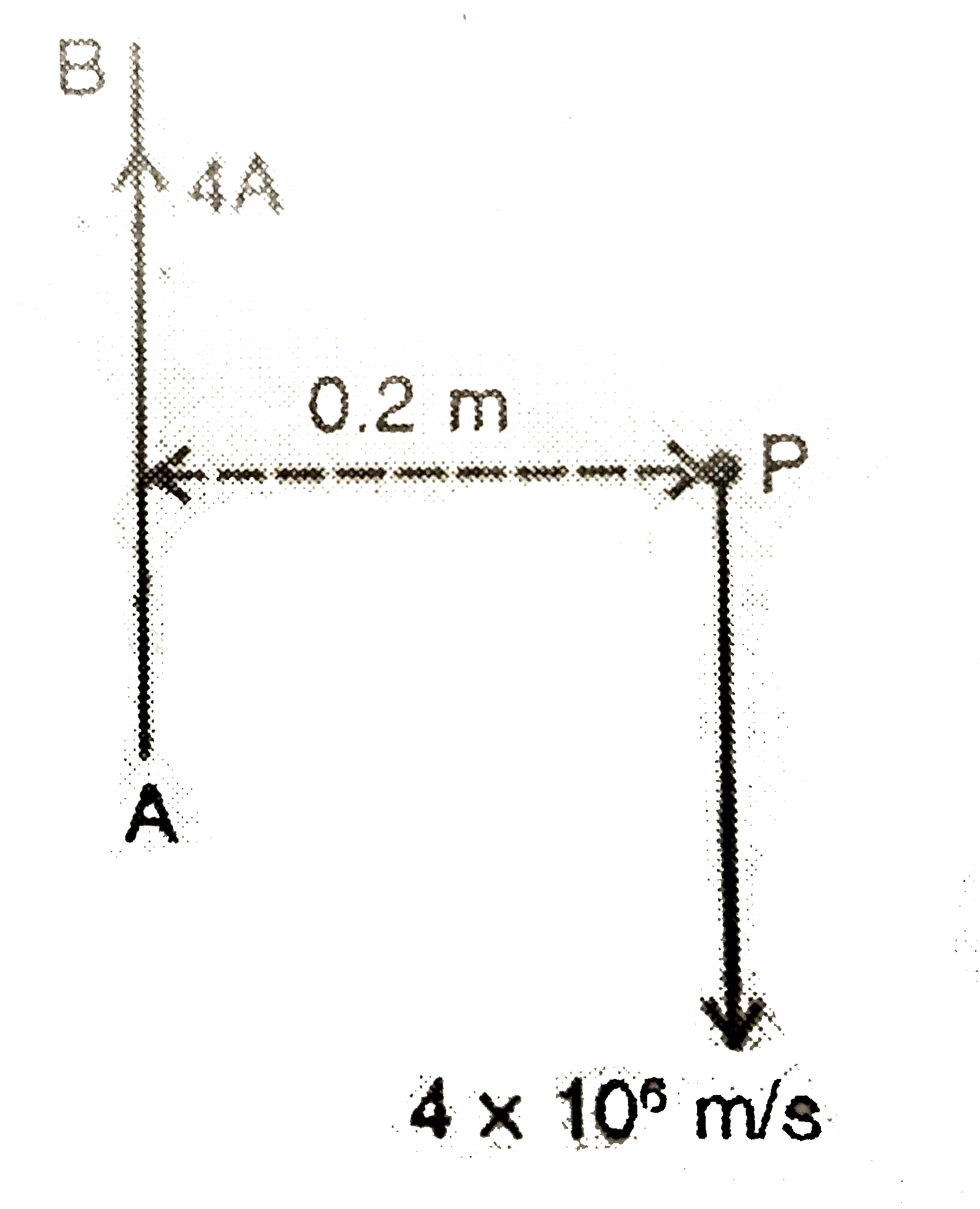
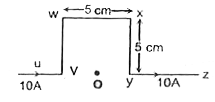
View SolutionThe resulting magnetic field at the point O due to the current carrying wire shown in the figure:
View SolutionCalculate the force on a current carrying wire in a uniform magnetic field as shown in Fig. 1.59.

View SolutionA staright wire of length (π2) meter is carrying a current of 2A and the magnetic field due to it is measured at a point distant 1cm from it. If the wire is to be bent into a circles and is to carry the same current as before, the ratio of the magnetic field at its centre to that obtained in the first case would be
View Solution
