Find the work done by the spring force as the bloc k is moved leftward from x1=15mm to xz=−10mm value of spring constant is 400
Hint : xi=+15 min
xf=−10 min
Ws=12kx21−12kx21
xi=+15mm,xf=−10mm
Ws=12kx2i−12kx2f
=12k(x2i−x2f)
=12×400×[(15×10−3)2−(−10×10−3)2]
=0.025J=25mJ
Similar Questions
In the above question, find the work done by the spring force as the block is moved leftward from x1=15mm to xz=−10mm.Take spring constant as 400 N/m.
View SolutionA particle is subjected to a force Fx that varies withes position as shown in figure. Find the work done by the force on the body as it moves
(a) from x=10.0m to x=5.0m,
(b) from x=5.0m to x=10.0m,
(c ) from x=10.0m to x=15.0m,
(d) what is the total work done by the force over the distance x=0 to x=15.0?
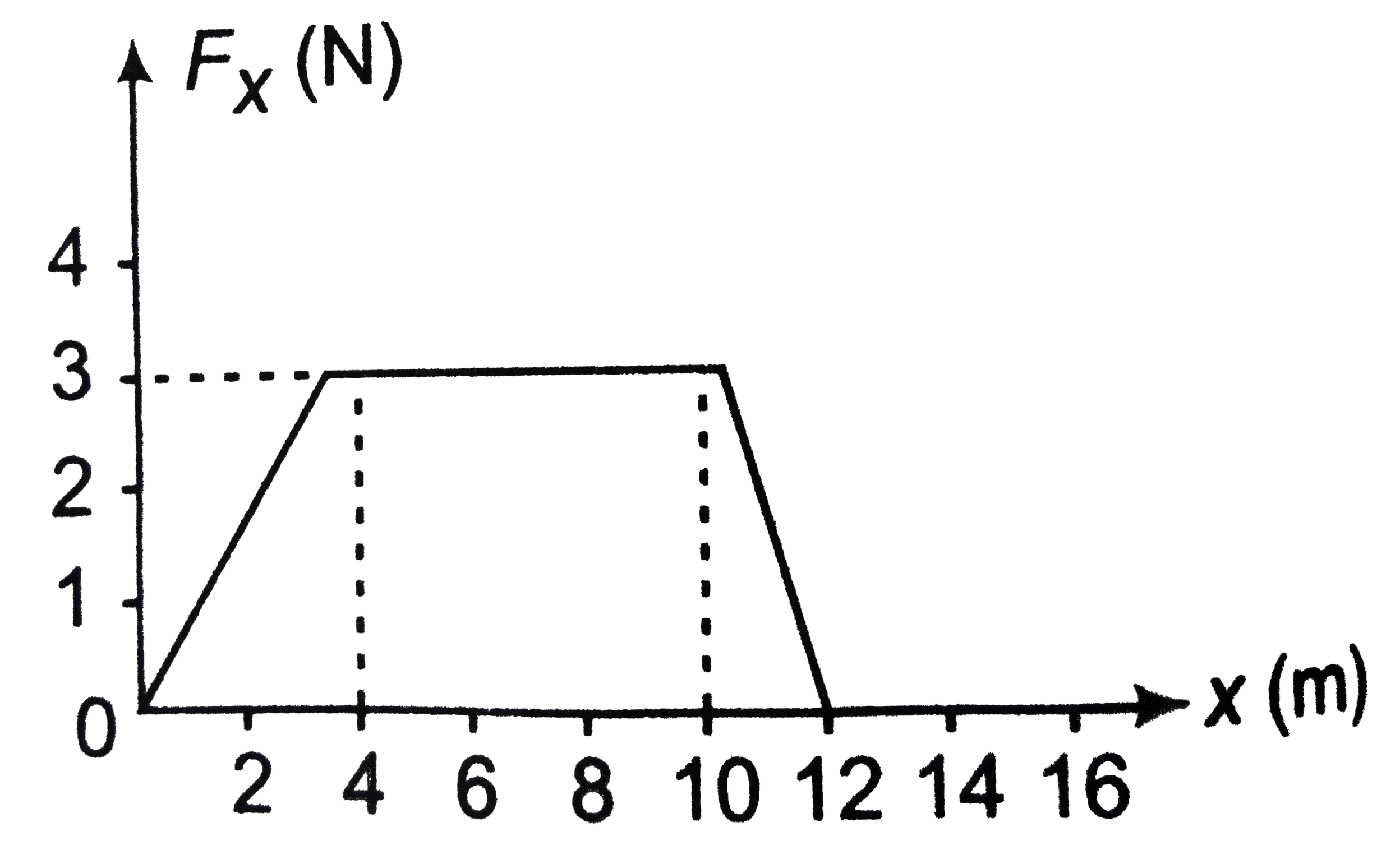 .View Solution
.View SolutionA force F=−kx2(x≠0) acts on a particle in x-direction. Find the work done by this force in displacing the particle from. x=+a to x=+2a. Where, k is a positive constant.
View SolutionA force F=−kx2(x≠0) acts on a particle in x-direction. Find the work done by this force in displacing the particle from. x=+a to x=2a. Here, k is a positive constant.
View SolutionConsider a block connected to a light spring of spring constant 100Nm−1. Now the block is displaced by applying a constant force F which gives zero resultant force when spring is stretched through 10 cm.
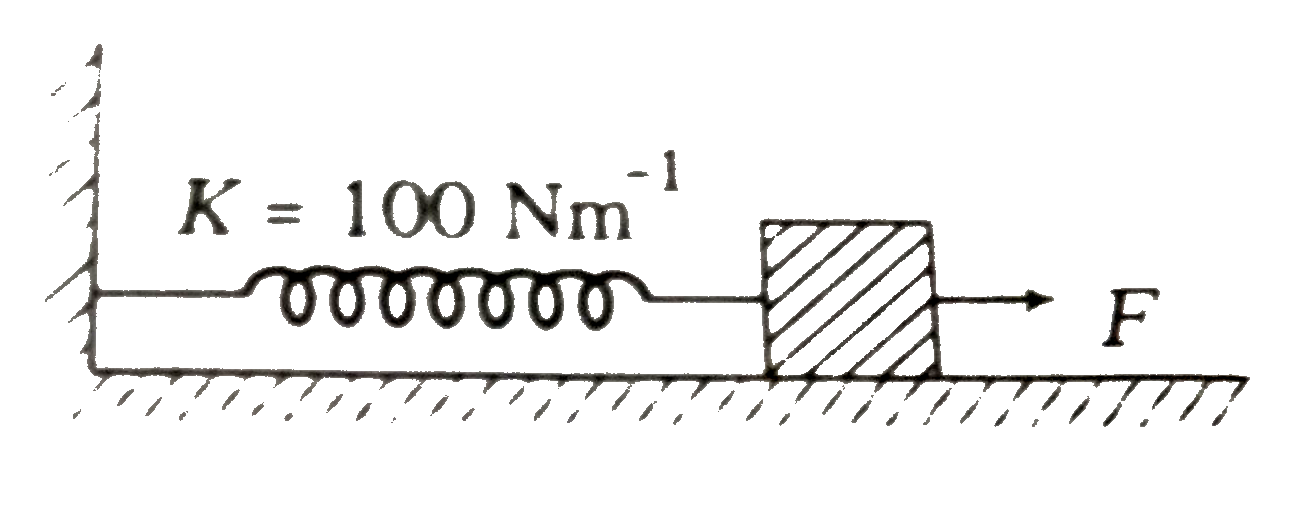
Evaluate
(i) Work done by the spring force when the block attains equilibrium.
(ii) Net work done on the block when it attains maximum speed.View SolutionA block of mass 0.1 kg attached to a spring of spring constant 400 N/m is putted rightward from x0=0 to x1=15 mm. Find the work done by spring force.
View SolutionThe block of mass M in figure −4.160, initially has a velocity vo to the right and its positionis much that the spring exerts no froce on it, i.e, the spring is not stretched or comkpressed. The block moves to the right a distance l before sttoping in the dotted position shown. The speing constant is k and the coefficeent of kinetic friction between block and table is μ. as the block moves the distance l, (a) what is the work done on it by the friction force ? (b) What is the work done on it by the spring force ? (c) are there other forces actionon the block, and if so what work do they do ? (d) what is the total work done on the block?
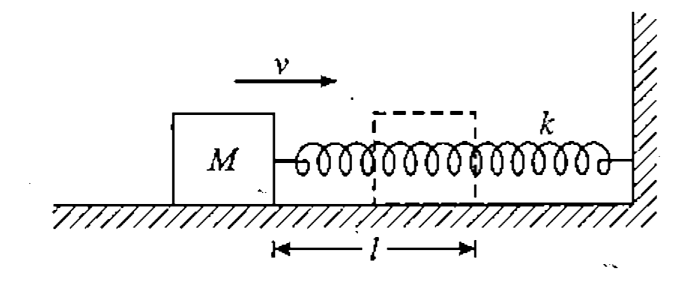 View Solution
View SolutionThe work done in extending a spring by x0 is W0. Find the work done in further extension x0.
View SolutionThe force exerted by a spring when it's displaced by x from its natural length is given by the equation F(x)=−kx, where k is a positive constant. What is the work done by a spring as it pushes out from x=−x2 to x=−x1 (where x2>x1)?
View SolutionThe spring force is given by F=−kx, here k is a constant and x is the deformation of spring. The F−x graph is
View Solution
