A ball dropped from height h on a horizontal floor goes up to the height 3h4 after hitting the floor. Fraction of energy of ball lost in the impact is
34
12
35
14
The correct Answer is:D
To find the fraction of energy lost by the ball after it hits the floor, we can follow these steps:
Step 1: Calculate the Initial Potential Energy (Ei)
When the ball is dropped from a height h, its initial potential energy (Ei) can be calculated using the formula:
Ei=mgh
where m is the mass of the ball, g is the acceleration due to gravity, and h is the height from which the ball is dropped.
Step 2: Calculate the Final Potential Energy (Ef)
After hitting the floor, the ball rises to a height of 3h4. The final potential energy (Ef) can be calculated as:
Ef=mg(3h4)=34mgh
Step 3: Calculate the Change in Energy (ΔE)
The change in energy (ΔE) is the difference between the initial potential energy and the final potential energy:
ΔE=Ei−Ef
Substituting the values we calculated:
ΔE=mgh−34mgh
Factoring out mgh:
ΔE=mgh(1−34)=mgh(14)
Step 4: Calculate the Fraction of Energy Lost
The fraction of energy lost can be calculated using the formula:
Fraction of energy lost=ΔEEi
Substituting the values we have:
Fraction of energy lost=14mghmgh
The mgh terms cancel out:
Fraction of energy lost=14
Conclusion
The fraction of energy lost by the ball after the impact is 14.
---
When the ball is dropped from a height h, its initial potential energy (Ei) can be calculated using the formula:
Ei=mgh
where m is the mass of the ball, g is the acceleration due to gravity, and h is the height from which the ball is dropped.
After hitting the floor, the ball rises to a height of 3h4. The final potential energy (Ef) can be calculated as:
Ef=mg(3h4)=34mgh
The change in energy (ΔE) is the difference between the initial potential energy and the final potential energy:
ΔE=Ei−Ef
Substituting the values we calculated:
ΔE=mgh−34mgh
Factoring out mgh:
ΔE=mgh(1−34)=mgh(14)
The fraction of energy lost can be calculated using the formula:
Fraction of energy lost=ΔEEi
Substituting the values we have:
Fraction of energy lost=14mghmgh
The mgh terms cancel out:
Fraction of energy lost=14
The fraction of energy lost by the ball after the impact is 14.
Topper's Solved these Questions
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - Assignment (SECTION - A)
64 Videos
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - Assignment (SECTION - B)
35 Videos
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - SECTION-J (AAKASH CHALLENGERS QUESTIONS)
14 Videos
- WAVESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WAVESEXERCISE - ASSIGNMENT ( SECTION-D ( Assertion - Reason Type Questions ))
12 Videos
Similar Questions
A ball dropped from a height of 2 m rebounds to a height of 1.5 m after hitting the ground. Then fraction of energy lost is
View SolutionA ball is dropped from height h on horizontal floor. If it loses 60% of its energy on hitting the floor then height upto which it will rise after first rebounce is
View Solution
Knowledge Check
A ball is dropped from a height h on the ground If the coefficient of restitution is e, the height to which the ball goes up after it rebounds for the nth time is
Ahe2nBhenCe2nhDhe2n
Two balls of same mass are dropped from the same height h, on to the floor. The first ball bounces to a height h/4, after the collision & the second ball to a height h/16. The impulse applied by the first & second ball on the floor are I1 and I2 respectively. Then :-
View SolutionA ball is dropped from a certain height on a horizontal floor. The coefficient of restitution between the ball and the floor is 12. The displacement time graph of the ball will be.
View SolutionA ball is allowed to fall from rest on a horizontal floor from a height of 10m. If there is 20% loss of energy due to impact, then after one impact ball will go upto
View SolutionA ball is dropped on a horizontal surface from height h. If it rebounds upto height h2 after first collision then coefficient of restitution between ball and surface is
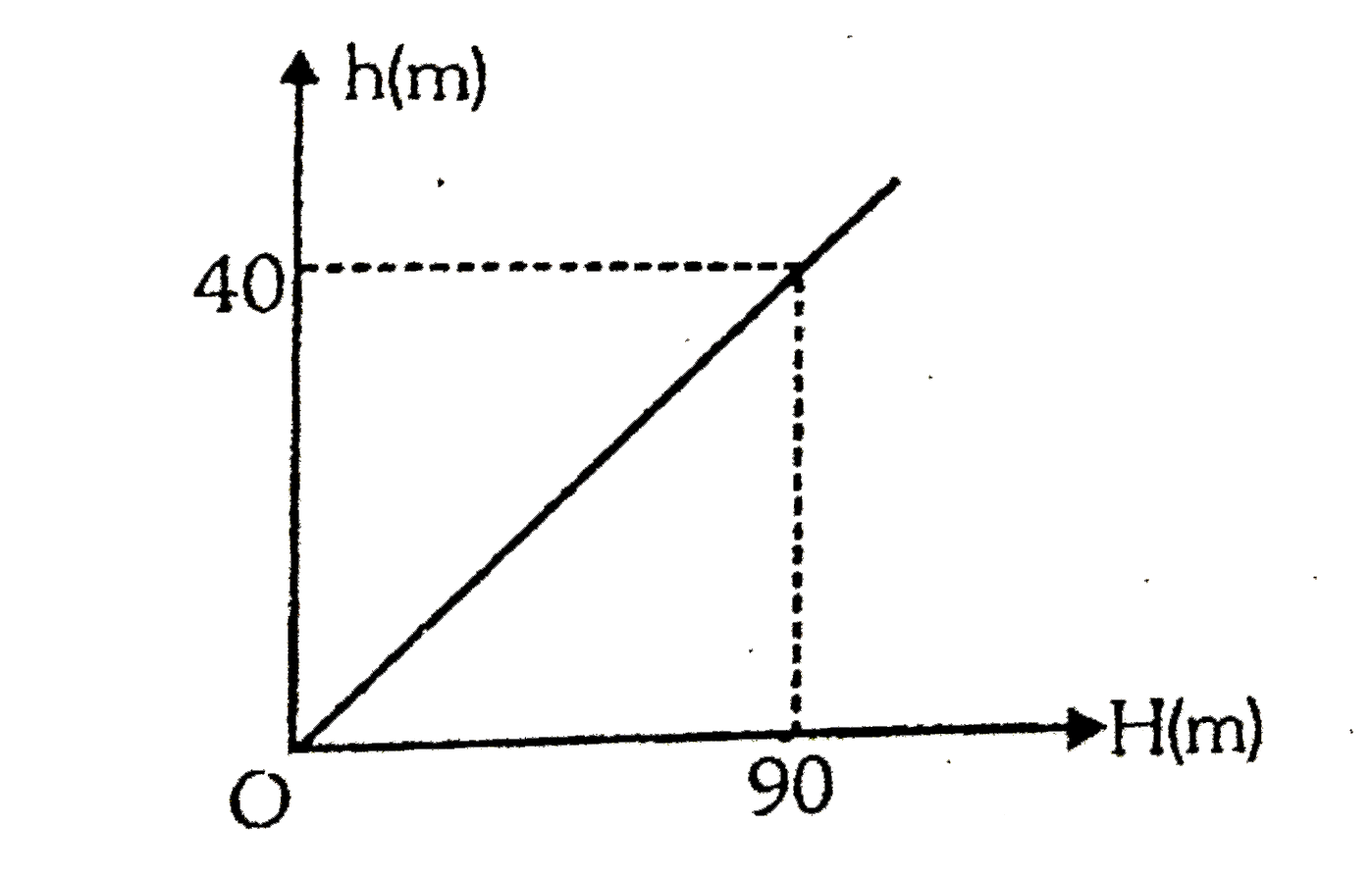
View SolutionA ball of mass 2kg dropped from a height H above a horizontal surface rebounds to a height h after one bounce. The graph that relates H to h is shown in figure. If the ball was dropped from an initial height of 81 m and made ten bounces, the kinetic energy of the ball immediately after the second impact with the surface was
View SolutionA small ball is dropped from rest from height 10 m on a horizontal floor. If coefficient of restitution between ground and body is 0.5 then find the maximum height it can rise after collision.
View SolutionA particle is dropped from rest from a height h0 on a horizontal floor. The coefficient of restitution between the floor and particle is e. Maximum height attained by the particle after first rebound is
View Solution
