The work done by an applied variable force F=x+x3 from x = 0 m to x = 2m, where x is displacement, is
6 J
8 J
10 J
12 J
The correct Answer is:A
To find the work done by the variable force F=x+x3 from x=0m to x=2m, we will follow these steps:
Step 1: Understand the relationship between work and force
The work done W by a variable force can be calculated using the integral of the force over the displacement. Mathematically, this is expressed as:
W=∫Fdx
Step 2: Substitute the given force into the equation
Given the force F=x+x3, we can substitute this into the work equation:
W=∫(x+x3)dx
Step 3: Set the limits of integration
The limits of integration are from x=0 to x=2:
W=∫20(x+x3)dx
Step 4: Break the integral into two parts
We can split the integral into two separate integrals:
W=∫20xdx+∫20x3dx
Step 5: Calculate the first integral
The first integral ∫xdx can be computed as follows:
∫xdx=x22∣∣20=222−022=42−0=2
Step 6: Calculate the second integral
The second integral ∫x3dx can be computed as:
∫x3dx=x44∣∣20=244−044=164−0=4
Step 7: Combine the results
Now, we can combine the results of the two integrals to find the total work done:
W=2+4=6Joules
Final Answer
The work done by the applied variable force from x=0m to x=2m is 6J.
---
The work done W by a variable force can be calculated using the integral of the force over the displacement. Mathematically, this is expressed as:
W=∫Fdx
Given the force F=x+x3, we can substitute this into the work equation:
W=∫(x+x3)dx
The limits of integration are from x=0 to x=2:
W=∫20(x+x3)dx
We can split the integral into two separate integrals:
W=∫20xdx+∫20x3dx
The first integral ∫xdx can be computed as follows:
∫xdx=x22∣∣20=222−022=42−0=2
The second integral ∫x3dx can be computed as:
∫x3dx=x44∣∣20=244−044=164−0=4
Now, we can combine the results of the two integrals to find the total work done:
W=2+4=6Joules
The work done by the applied variable force from x=0m to x=2m is 6J.
Topper's Solved these Questions
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - Assignment (SECTION - D)
13 Videos
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - Assignment (SECTION - B)
35 Videos
- WAVESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WAVESEXERCISE - ASSIGNMENT ( SECTION-D ( Assertion - Reason Type Questions ))
12 Videos
Similar Questions
A force F=−kx2(x≠0) acts on a particle in x-direction. Find the work done by this force in displacing the particle from. x=+a to x=+2a. Where, k is a positive constant.
View SolutionA particle is subjected to a force Fx that varies withes position as shown in figure. Find the work done by the force on the body as it moves
(a) from x=10.0m to x=5.0m,
(b) from x=5.0m to x=10.0m,
(c ) from x=10.0m to x=15.0m,
(d) what is the total work done by the force over the distance x=0 to x=15.0?
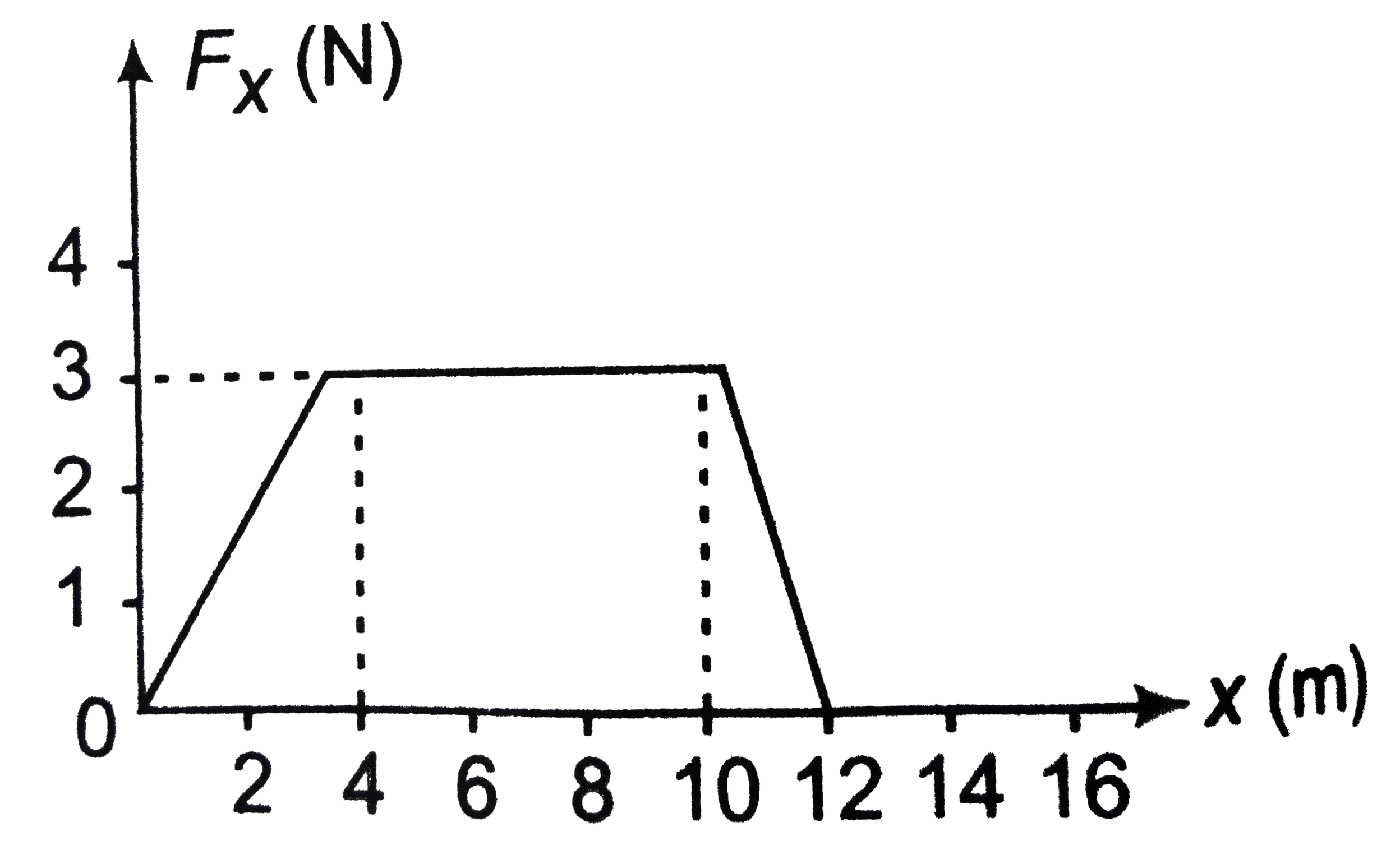 .
.
View SolutionA force F=−kx2(x≠0) acts on a particle in x-direction. Find the work done by this force in displacing the particle from. x=+a to x=2a. Here, k is a positive constant.
View SolutionThe work done by a force →F=(−6x3ˆi) N in displacing a particle from x = 4m to x = - 2m is
View SolutionThe work done by a force →F=(−6x2ˆi)N in displacing a particle from x = 4mtox = -2mis
View SolutionA variable force F acts along the x - axis given by F=(3x2)−2x+1N. The work done by the force when a particle of mass 100 g moves from x = 50 cm to x = 100 cm is
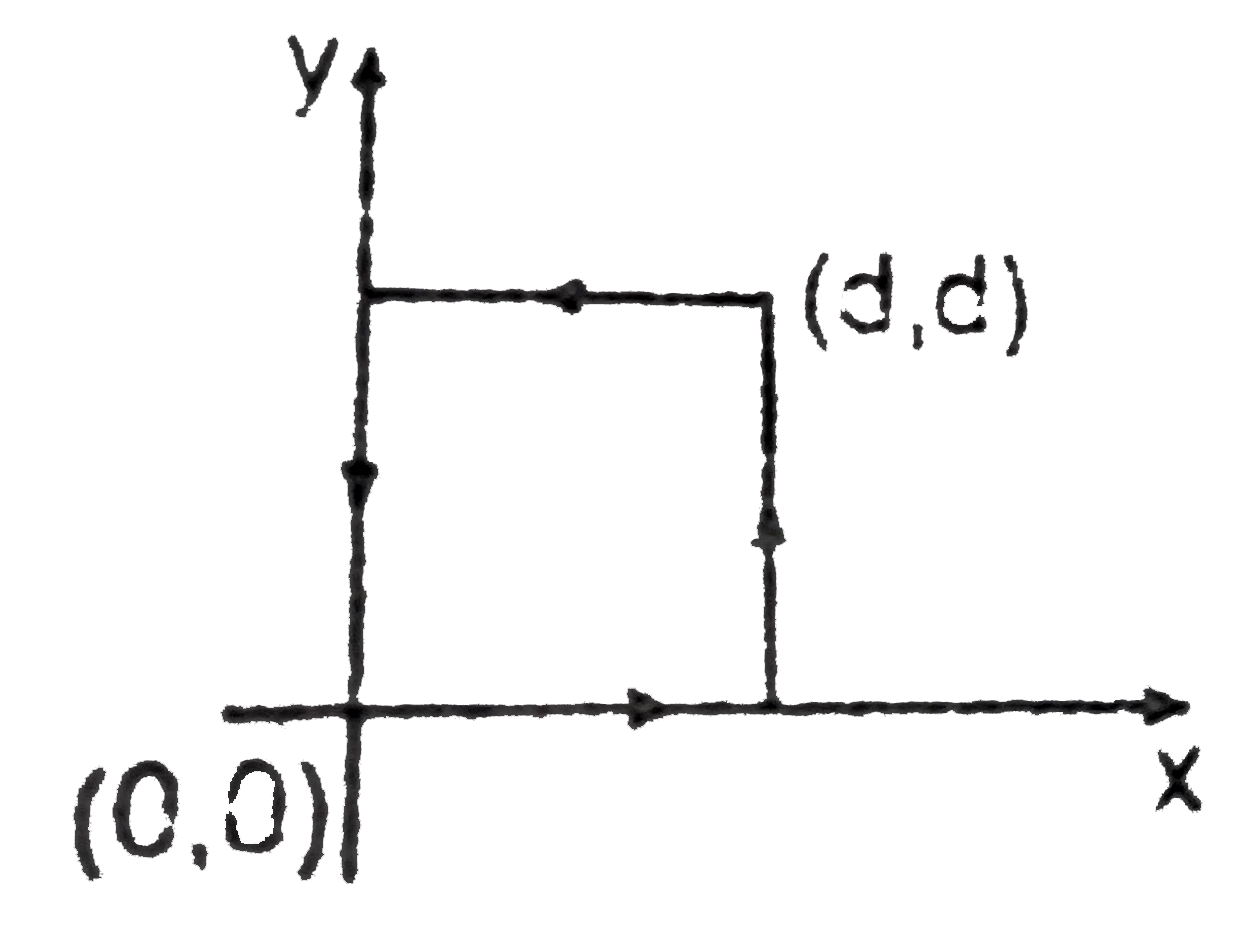
View SolutionThe work done by the force F=A(y2ˆi+2x2ˆj), where A is a constant and x & y are in meters around the path shown in
View SolutionA particale moves under the effect of a force F=Cx from x=0 to x=x1. The work down in the process is
View SolutionAn object of mass 8 kg starts to move from rest under the action of a variable force F=3xN where x is the distance (in m) covered by the object. If initially, the position of the object is x = 2 m, then find its speed (in m s−1) when it crosses x = 10 m.
View SolutionA force (F) acting on a particle varies work done by a particle varies with the with the position x as shown in figure
 .
.
Find the work done by by force in displacing the particle from .
(a) x=−2m to x=0
(b) x=0 to x=2m..
View Solution
