A capacitor is half filied with a dielectric (K = 2 ) as shown in figure A. if the same capacitor is to be filied with same , what would be the thickness of dielectric so that capacitor still has same capacity ?
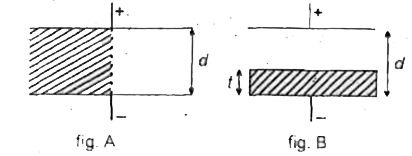
2d/3
3d/2
3d/4
4d/3
The correct Answer is:A
Step by step video & image solution for A capacitor is half filied with a dielectric (K = 2 ) as shown in figure A. if the same capacitor is to be filied with same , what would be the thickness of dielectric so that capacitor still has same capacity ? by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - ASSIGNMENT SECTION - B
38 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - ASSIGNMENT SECTION - C
53 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - EXERCISE
20 Videos
- ELECTROMAGNETIC WAVESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - ASSIGNMENT SECTION - D Assertion-Reason Type Questions
25 Videos
- GRAVITATION BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - GRAVITATION EXERCISE - ASSIGNMENT SECTION - D (ASSERTION-REASON TYPE QUESTIONS)
15 Videos
Similar Questions
A parallel plate capacitor has two layers of dielectrics as shown in figure. This capacitor is connected across a battery, then the ratio of potential difference across the dielectric layers is

View SolutionConsider a disconnected plate capacitor of capacity 10μF with air filled in the gap between the plates. Now one-half of the space between the plates is filled with a dielectric of dielectric constant 4 as shown in .The capacity of the capacitor changes to
 .
.
View SolutionIn the figure, a capacitor is field with dielectrics. The resultant capacitance is

View SolutionA parallel plate capacitor has a dielectric slab of dielectric constant K between its plates that covers 1/3 of the area of its plates, as shown in the figure. The total capacitance of the capacitor is C while that of the portion with dielectric in between is C1. When the capacitor is charged, the plate area covered by the dielectric gets charge Q1 and the rest of the area gets charge Q2. The electric field in the dielectric is E1 and that in the other portion is E2. Choose the correct option/options, ignoring edge effects.

View SolutionA parallel plate capacitor of capacitance C (without dielectric) is filled by dielectric slabs as shown in figure. Then the new capacitance of the capacitor is

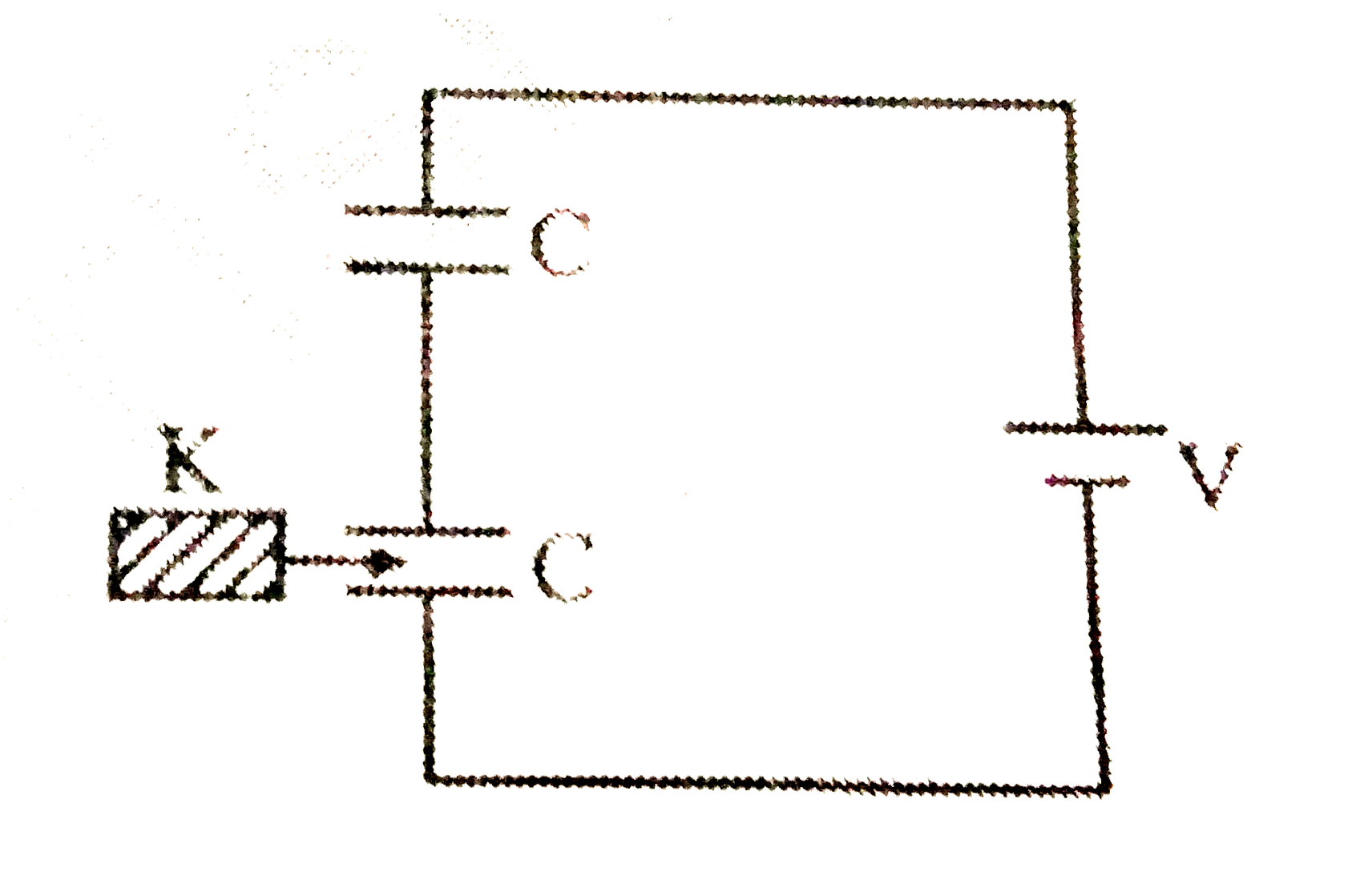
View SolutionThe work done in placing the dielectric slab inside one of the capacitors as shown in diagram
View SolutionA capacitor of plate area A and separation d is filled with two dielectrics of dielectric constant K1=6andK2=4. New capacitance will be

View SolutionConsider these three statements for a capacitor
STATEMENT-1 : Capacitance of a capacitor must increase when a dielectric is inserted in between the capacitor plates.
STATEMENT-2 : Potential differenece across a charged capacitor must increase if a dielectric is inserted in between the capacitor plates.
STATEMENT-3 : Electrostatic energy stored by the capacitor may increase if a dielectric inserted in between the capacitor plates
View SolutionFind the capacitances of the capacitance of the capacitors shown In figure .The plate area is Aand the separation between the plate is d. Different dielectric slabe in a particular part of the figure area of the same thickness and the entire gap between the plate is filled with the dielectric slabs.

View SolutionTwo identical parallel plate capacitors, of capacitance C each, have plates of area A, separated by a distance d. The space between the plates of the two capacitors, is filled with three dielectrics, of equal thickness and dielectric constants K1,K2andK3. The first capacitor is filled as shown in fig. I, and the second one is filled as shown in fig. II. If these two modified capacitors are charged by the same potential V, the ratio of the energy stored in the two, would be (E1 refers to capacitor (I) and E2 to capacitor (II)):
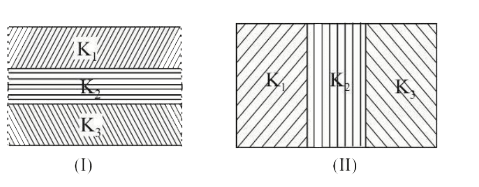
View Solution
