A ray of light is incident from a denser to a rarer medium. The critical angle for total internal reflection is θic and Brewster's angle of incidence is θiB such that sinθicsinθiB=η=1.28 . The relative refractive index of the two media is
0.4
0.2
0.9
0.8
The correct Answer is:D
To solve the problem, we need to find the relative refractive index of two media given the relationship between the critical angle and Brewster's angle. Let's denote the refractive indices of the denser medium as n1 and the rarer medium as n2.
1. Understanding the Critical Angle:
The critical angle θic for total internal reflection is given by Snell's law:
n1sin(θic)=n2sin(90∘)
Since sin(90∘)=1, we can rewrite this as:
sin(θic)=n2n1(1)
2. Understanding Brewster's Angle:
Brewster's angle θiB is given by:
tan(θiB)=n2n1
This can also be expressed in terms of sine and cosine:
sin(θiB)=n2√n21+n22(2)
3. Using the Given Relationship:
We are given that:
sin(θic)sin(θiB)=1.28
Substituting equations (1) and (2) into this relationship gives:
n2n1n2√n21+n22=1.28
Simplifying this, we have:
n2√n21+n22n2n1=1.28
Cancelling n2 (assuming n2≠0):
√n21+n22n1=1.28
4. Squaring Both Sides:
Squaring both sides results in:
n21+n22n21=1.282
Calculating 1.282:
1.282=1.6384
Thus, we have:
1+n22n21=1.6384
Rearranging gives:
n22n21=1.6384−1=0.6384
5. Finding the Ratio of Refractive Indices:
Taking the square root of both sides:
n2n1=√0.6384≈0.798
6. Conclusion:
The relative refractive index of the two media is:
n2n1≈0.8
Final Answer:
The relative refractive index of the two media is approximately 0.8.
The critical angle θic for total internal reflection is given by Snell's law:
n1sin(θic)=n2sin(90∘)
Since sin(90∘)=1, we can rewrite this as:
sin(θic)=n2n1(1)
Brewster's angle θiB is given by:
tan(θiB)=n2n1
This can also be expressed in terms of sine and cosine:
sin(θiB)=n2√n21+n22(2)
We are given that:
sin(θic)sin(θiB)=1.28
Substituting equations (1) and (2) into this relationship gives:
n2n1n2√n21+n22=1.28
Simplifying this, we have:
n2√n21+n22n2n1=1.28
Cancelling n2 (assuming n2≠0):
√n21+n22n1=1.28
Squaring both sides results in:
n21+n22n21=1.282
Calculating 1.282:
1.282=1.6384
Thus, we have:
1+n22n21=1.6384
Rearranging gives:
n22n21=1.6384−1=0.6384
Taking the square root of both sides:
n2n1=√0.6384≈0.798
The relative refractive index of the two media is:
n2n1≈0.8
The relative refractive index of the two media is approximately 0.8.
Similar Questions
A ray of light travels from an optically denser to rarer medium. The critical angle of the two media is C. The maximum possible deviation of the ray will be
View SolutionA ray of light passes from vaccum into a medium of refractive index n. If the angle of incidence is twice the angle of refraction, then the angle of incidence is
View SolutionA ray of light is incident on a transparent medium at polarizing angle. What is the angle between the reflected ray and the refracted ray .
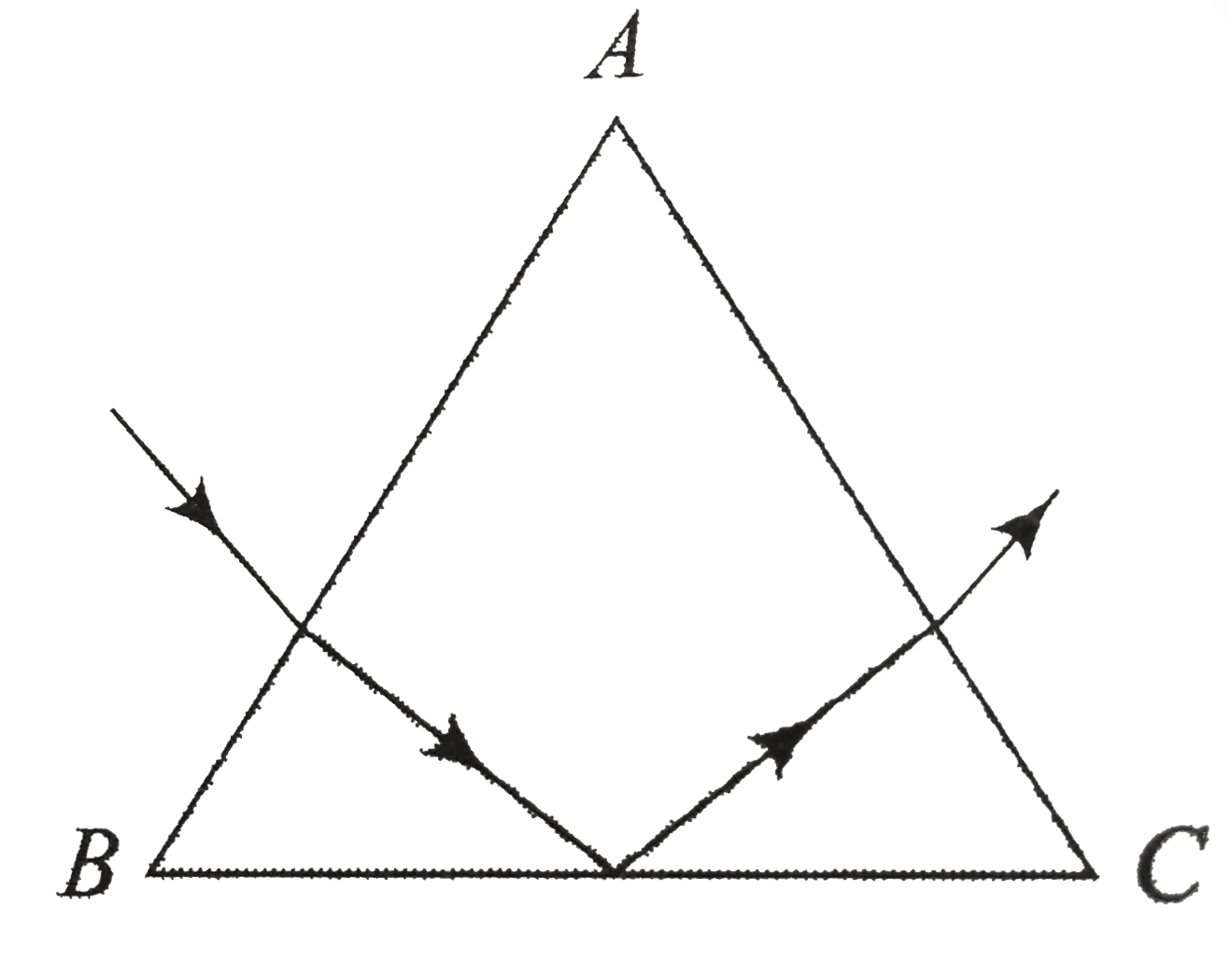
View SolutionThe path of a ray of light passing through an equilateral glass prism ABC is shown in figure. The ray of light is incident on face BC at the critical angle for just total internal reflection. The total internal reflection. The total angle of deviation after the refraction at face AC is 108∘. Calculate the refractive index of the glass.
View SolutionIf the critical angle for total internal reflection, from a medium to vacuum is 30∘, then velocity of light in the medium is
View SolutionFor total internal reflection to take place, the angle of incidence i and the refractive index μ of the medium must satisfy the inequality
View SolutionA ray of light passes from glass, having a refractive index of 1.6, to air. The angle of incidence for which the angle of refraction is twice the angle of incidence is
View SolutionA light ray is incident fromt a denser medium on the boundary separating it from a rarer medium at an angle of incidence equal to the critical angle. What is the angle of refraction for the ray ?
View SolutionA ray of light is incident on a glass prism of refractive index μ and refractive angle A. If it just suffers total internal reflection at the other face, obtain an expression relating the angle of incidence , angle of prism and critical angle.
View SolutionUnder what conditions is the phenomenon of total internal reflection between the critical angle of incidence and the refractive index of the medium.
View Solution
