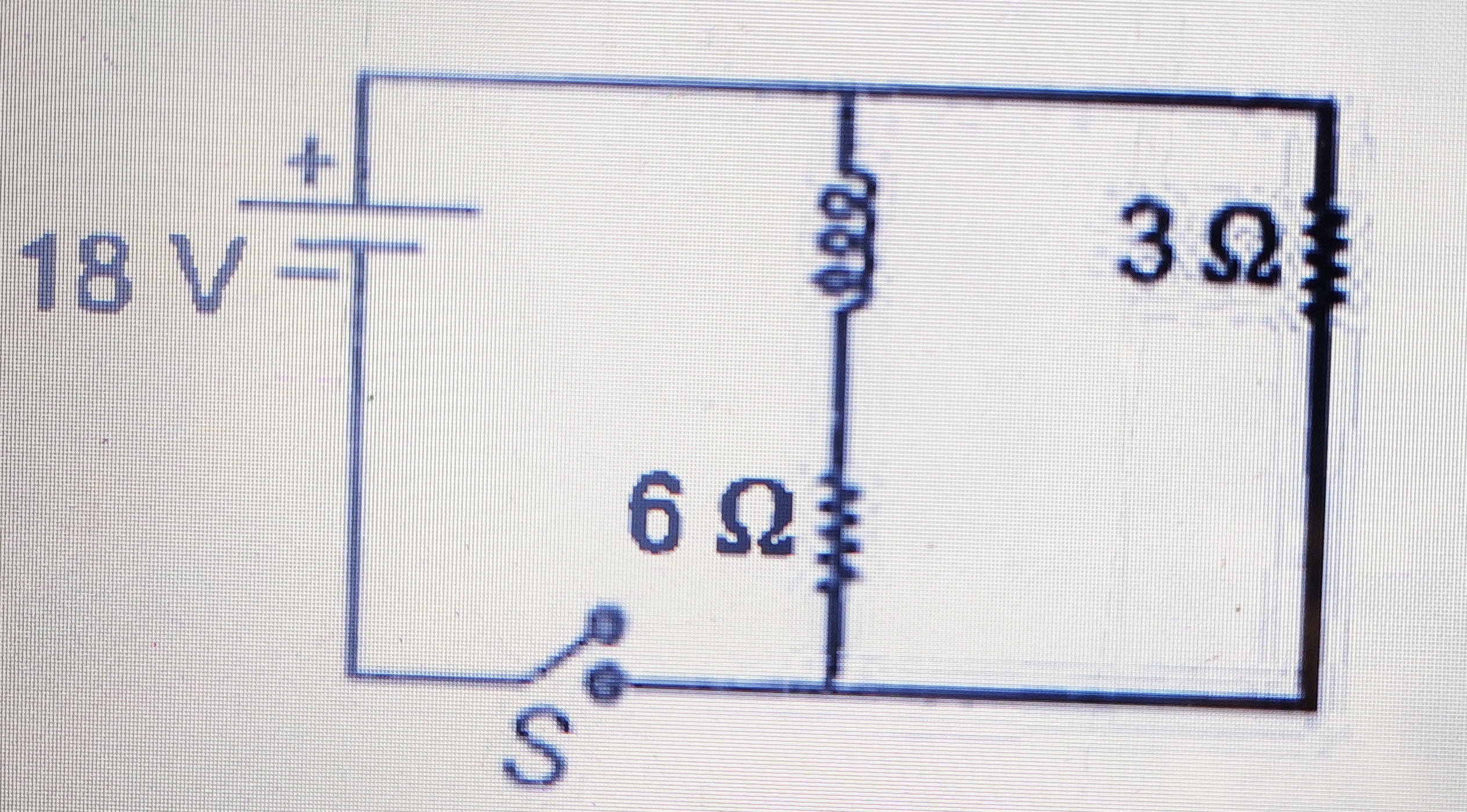
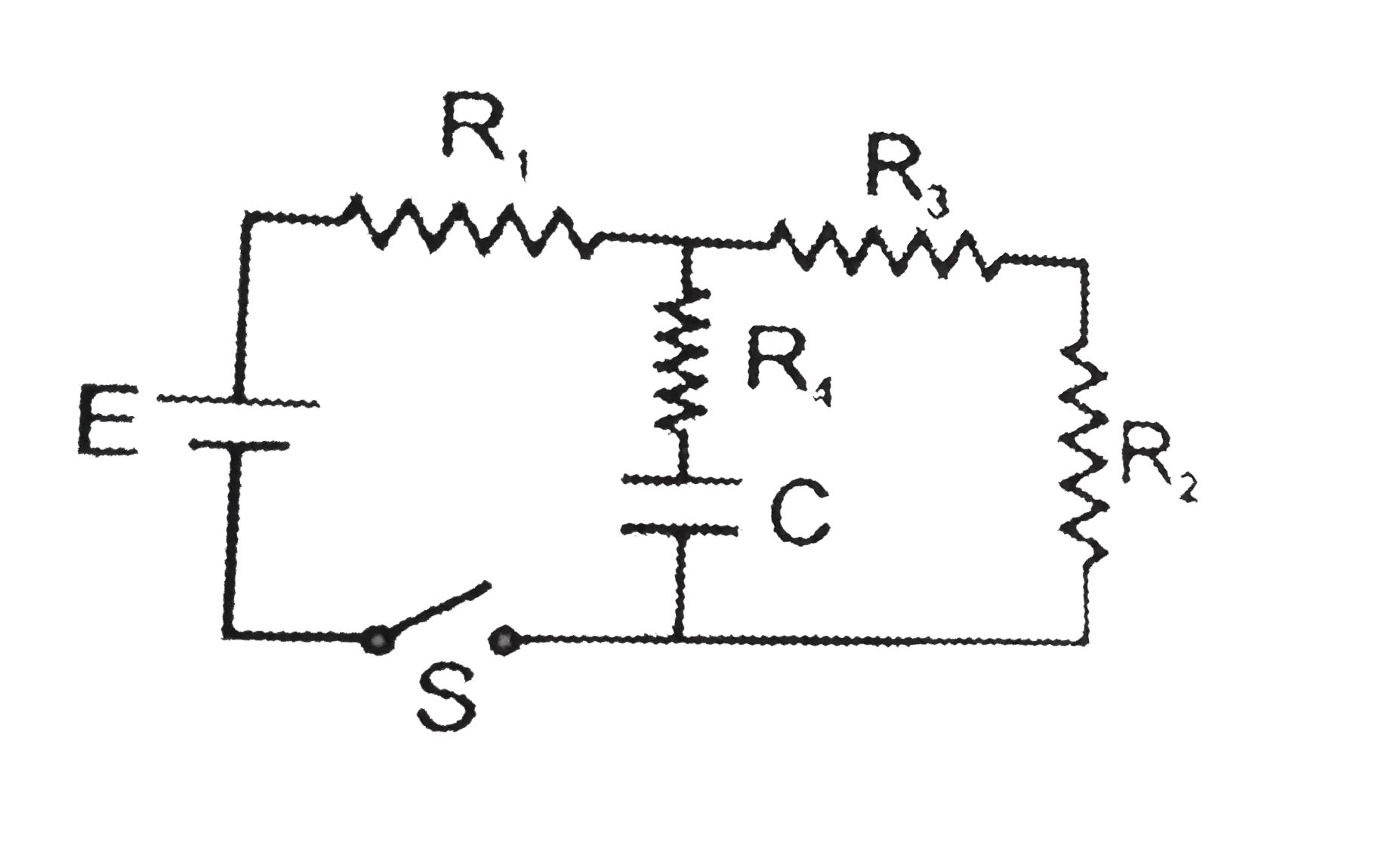
The ratio of currents passing through resistance R_1 as shown in the figure, before and after switch S is closed, is (The potentials at A and B remain unchanged)
2:01
1:01
3:01
1:07
To solve the problem of finding the ratio of currents passing through resistance R1 before and after the switch S is closed, we will follow these steps:
Step 1: Understand the Circuit Configuration
Before the switch S is closed, the circuit consists of two resistors R1 (2 ohms) in series. The potentials at points A and B are 30 volts and 10 volts, respectively.
Step 2: Calculate Current Before the Switch is Closed
When the switch is open, the total resistance in the circuit is the sum of the two resistors:
Rtotal=R1+R2=2Ω+2Ω=4Ω
Using Ohm's law, the current I flowing through the circuit can be calculated as:
I=VR=30V−10V4Ω=20V4Ω=5A
Step 3: Analyze the Circuit After the Switch is Closed
When the switch S is closed, the circuit configuration changes. The 3-ohm resistor is now included in the circuit. The potential at point B is grounded (0 volts).
Step 4: Set Up the Equation for Currents After the Switch is Closed
Let x be the potential at the junction X (between the 3-ohm resistor and the two 2-ohm resistors). The currents can be expressed as:
- Current through the 2-ohm resistor (from A to X):
I1=30V−x2Ω
- Current through the 3-ohm resistor (from X to ground):
I2=x−03Ω
- Current through the other 2-ohm resistor (from X to B):
I3=x−10V2Ω
Step 5: Apply Kirchhoff's Current Law at Junction X
According to Kirchhoff's Current Law:
I=I1=I2+I3
Substituting the expressions for I1, I2, and I3:
30−x2=x3+x−102
Step 6: Solve the Equation
Multiply through by 6 to eliminate the fractions:
3(30−x)=2x+3(x−10)
Expanding and simplifying:
90−3x=2x+3x−30
90−3x=5x−30
Bringing all terms involving x to one side:
90+30=5x+3x
120=8x⟹x=15V
Step 7: Calculate the Current Through R1 After the Switch is Closed
Now, we can calculate the current through R1:
I=15V−10V2Ω=5V2Ω=2.5A
Step 8: Calculate the Ratio of Currents
Now, we have:
- Current before the switch is closed: Iinitial=5A
- Current after the switch is closed: Ifinal=2.5A
The ratio of currents is:
IinitialIfinal=5A2.5A=2
Thus, the ratio of currents passing through resistance R1 before and after the switch is closed is:
Ratio=2:1
Final Answer
The ratio of currents passing through resistance R1 before and after the switch S is closed is 2:1.
Before the switch S is closed, the circuit consists of two resistors R1 (2 ohms) in series. The potentials at points A and B are 30 volts and 10 volts, respectively.
When the switch is open, the total resistance in the circuit is the sum of the two resistors:
Rtotal=R1+R2=2Ω+2Ω=4Ω
Using Ohm's law, the current I flowing through the circuit can be calculated as:
I=VR=30V−10V4Ω=20V4Ω=5A
When the switch S is closed, the circuit configuration changes. The 3-ohm resistor is now included in the circuit. The potential at point B is grounded (0 volts).
Let x be the potential at the junction X (between the 3-ohm resistor and the two 2-ohm resistors). The currents can be expressed as:
- Current through the 2-ohm resistor (from A to X):
I1=30V−x2Ω
- Current through the 3-ohm resistor (from X to ground):
I2=x−03Ω
- Current through the other 2-ohm resistor (from X to B):
I3=x−10V2Ω
According to Kirchhoff's Current Law:
I=I1=I2+I3
Substituting the expressions for I1, I2, and I3:
30−x2=x3+x−102
Multiply through by 6 to eliminate the fractions:
3(30−x)=2x+3(x−10)
Expanding and simplifying:
90−3x=2x+3x−30
90−3x=5x−30
Bringing all terms involving x to one side:
90+30=5x+3x
120=8x⟹x=15V
Now, we can calculate the current through R1:
I=15V−10V2Ω=5V2Ω=2.5A
Now, we have:
- Current before the switch is closed: Iinitial=5A
- Current after the switch is closed: Ifinal=2.5A
IinitialIfinal=5A2.5A=2
Ratio=2:1
The ratio of currents passing through resistance R1 before and after the switch S is closed is 2:1.
Topper's Solved these Questions
- TEST 1BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - TEST 1EXERCISE - EXERCISE
21 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Try Yourself
63 Videos
- TEST 2BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - TEST 2EXERCISE - Exercise
308 Videos
Similar Questions
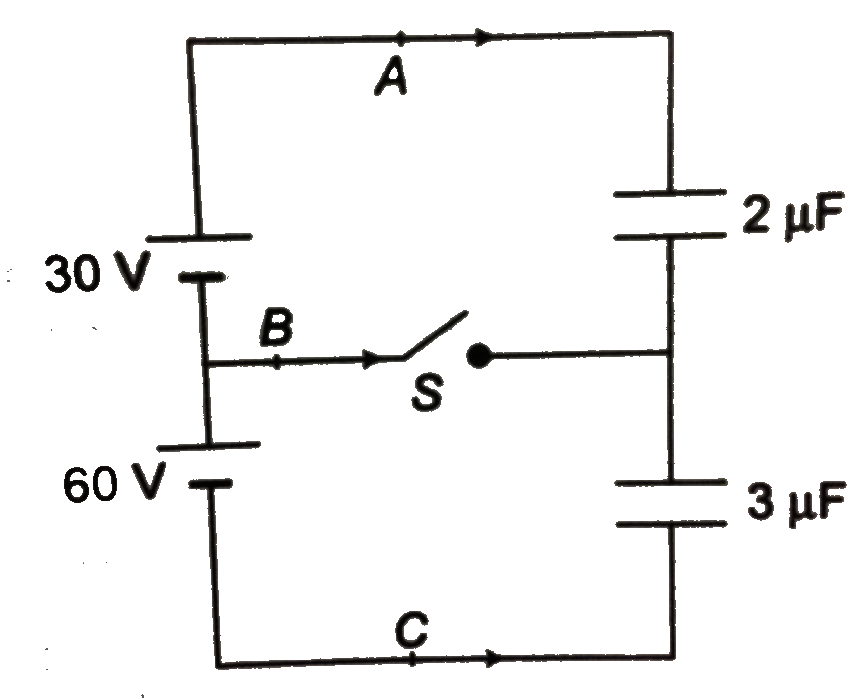
What charges will flow through A,B and C in the direction shown in the figure when switch S is closed?
View SolutionThe current through the battery just after the switch S is Closed is (the capacitors are initially uncharged )
_PHY_E01_002_Q01.png)
View SolutionDetermine the current through the battery in the circuit shown in figure.
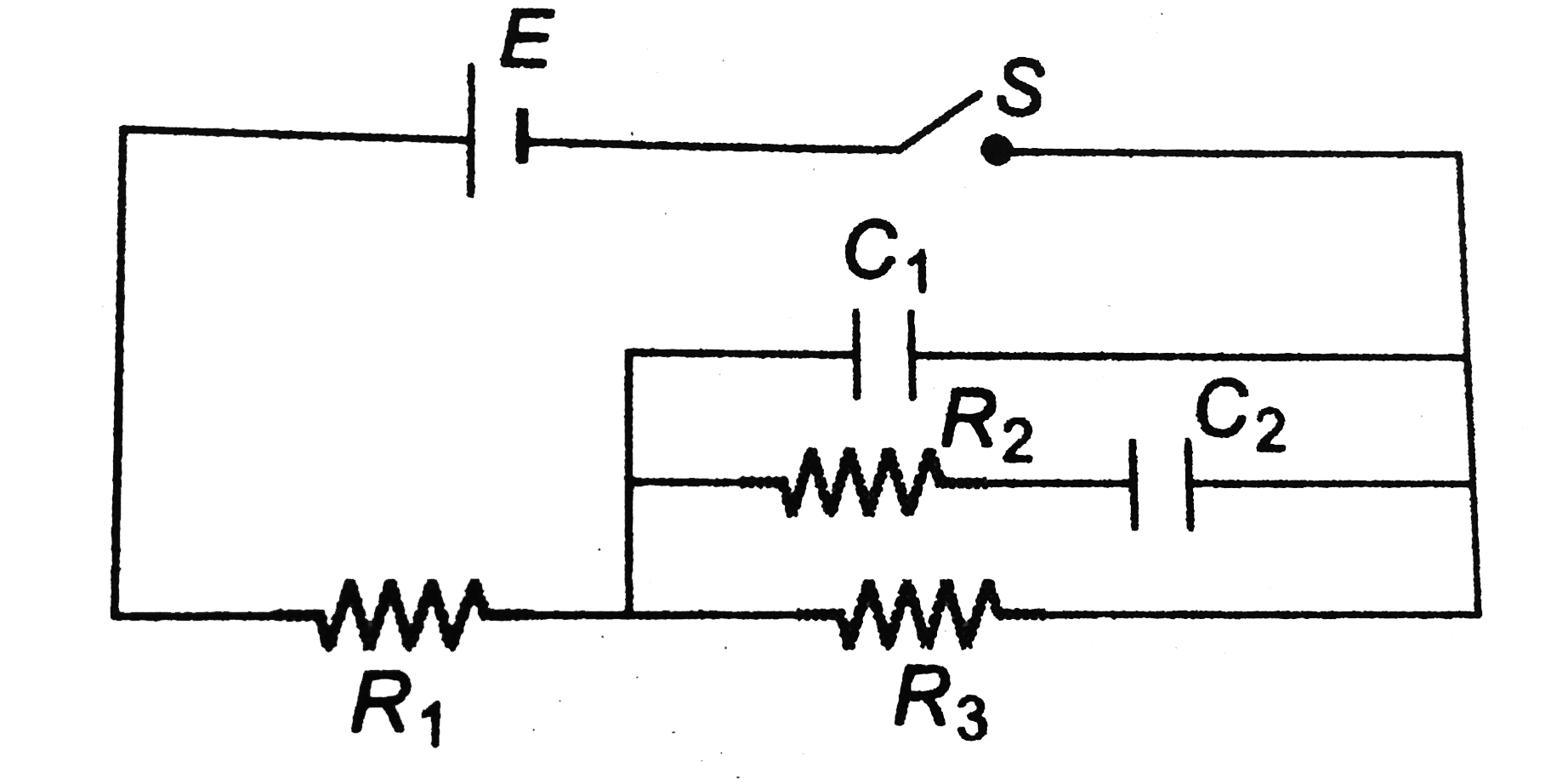
(a) immediately after the switch S is closed
(b) after a long time.
View SolutionIn the following circuit the value of current i through the battery just after switch S is closed is
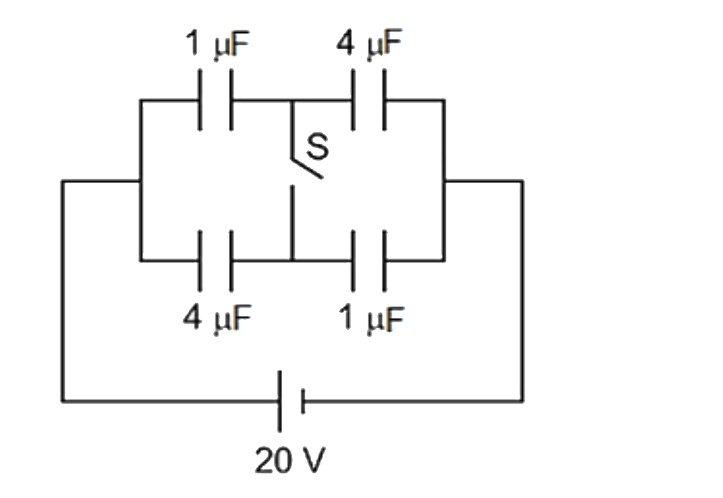
View SolutionFor the circuit shown in the figure , the charge flown through the switch after it is closed is n μC. Find the value of n.
View SolutionFor the circuit shown in figure below, at t = 0, switch is closed, the initial current through resistor and final charge on capacitor are

View SolutionConsider the circuit shown in figure, after switch S is closed.

What amount of charge will flow through the switch?
View SolutionThe ratio of initial to final current through the battery when the switch is closed in the figure is
View SolutionIn the circuit shown in figure the switch S is closed at t = 0. A long time after closing the switch
View SolutionA resistance of frustum shape is shown in figure. If a current i passes through the resistance, the electric field at A and B are related as -
View Solution
