Question

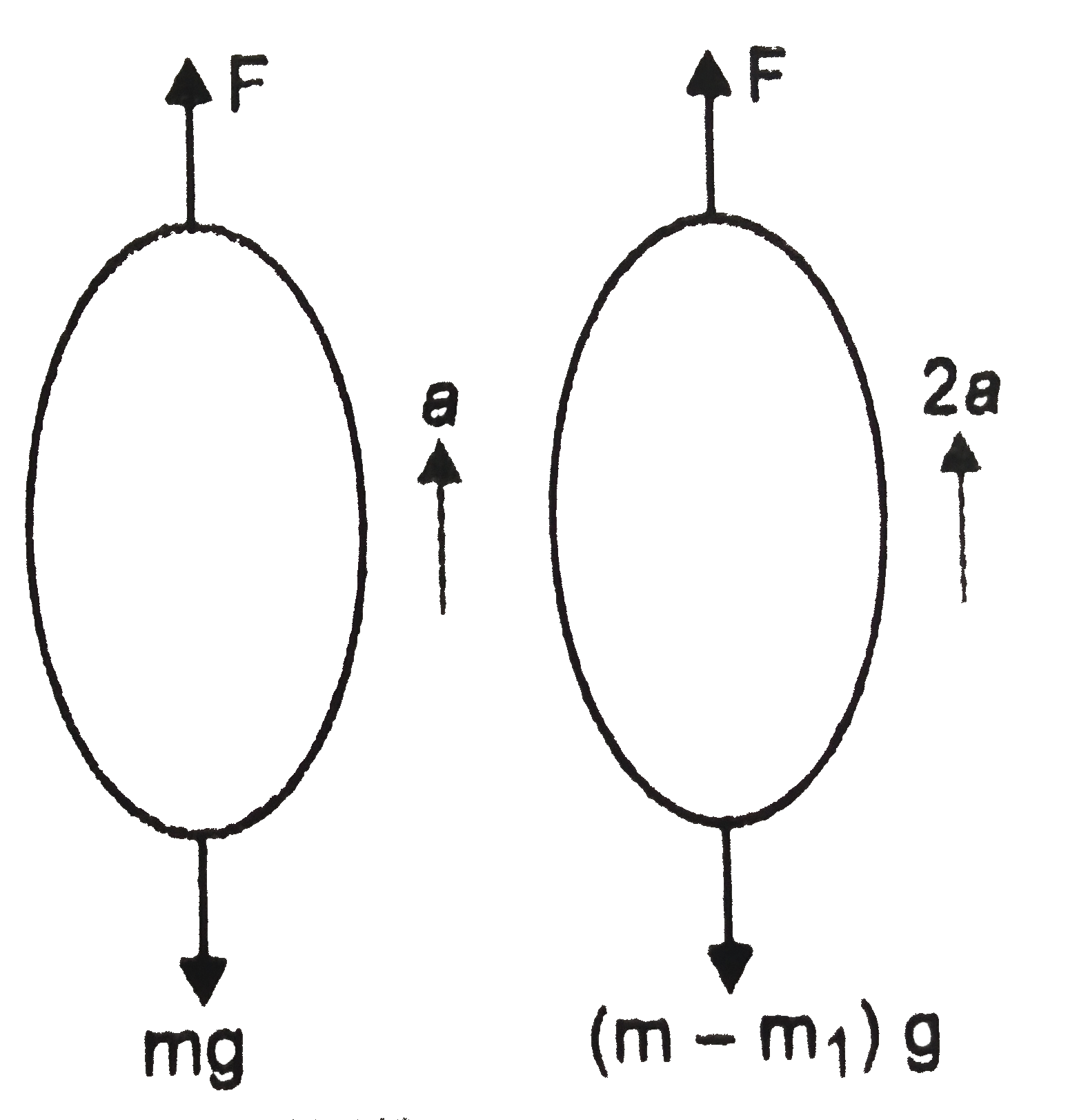
A balloon of mass m is descending down with an acceleration How much mass should be $\frac{g}{2}$ removed from it so that it starts moving up with same acceleration?

Options

A. `1/2 J`
B. `3/2 J`
C. `9/4 J`
D. `9/2 J`

Explanation

To solve the problem step by step, we will analyze the forces acting on the balloon in both scenarios: when it is descending and when it is ascending.

Step 1: Understand the forces acting on the balloon

The balloon has a mass \( m \) and is descending with an acceleration of \( \frac{g}{2} \). The force due to gravity acting on the balloon is given by:
\( F_g = mg \)

Step 2: Set up the equation for the descending balloon

When the balloon is descending, the net force acting on it can be expressed as:
\( F - mg = -ma \)
Here, \( a = \frac{g}{2} \) (downward acceleration), so:
\( F - mg = -m \left(\frac{g}{2}\right) \)

Step 3: Rearranging the equation for the descending balloon

Rearranging the equation gives:
\( F = mg - m\left(\frac{g}{2}\right) \)
\( F = mg - \frac{mg}{2} \)
\( F = \frac{mg}{2} \)

Step 4: Set up the equation for the ascending balloon

Now, let’s consider the case when we remove a mass \( x \) from the balloon. The new mass of the balloon becomes \( m - x \). The balloon now moves upward with the same acceleration \( \frac{g}{2} \). The net force equation for the ascending balloon is:
\( F - (m - x)g = (m - x)\left(\frac{g}{2}\right) \)

Step 5: Rearranging the equation for the ascending balloon

Rearranging this equation gives:
\( F = (m - x)g + (m - x)\left(\frac{g}{2}\right) \)
\( F = (m - x)g\left(1 + \frac{1}{2}\right) \)
\( F = (m - x)\left(\frac{3g}{2}\right) \)

Step 6: Equate the forces from both scenarios

Since we have two expressions for \( F \):
\( \frac{mg}{2} = (m - x)\left(\frac{3g}{2}\right) \)

Step 7: Cancel \( g \) from both sides

Dividing both sides by \( \frac{g}{2} \):
\( 1 = 3(m - x) \)

Step 8: Solve for \( x \)

Expanding and rearranging gives:
\( 1 = 3m - 3x \)
\( 3x = 3m - 1 \)
\( x = m - \frac{1}{3} \)

Step 9: Final answer

Thus, the mass that should be removed from the balloon is:
\( x = \frac{2m}{3} \)